Burosch-Homebutton

Audio-Technik Grundlagenwissen vom Spezialisten

Audio-Technik Grundlagenwissen vom Spezialisten

BUROSCH begann seinerzeit mit dem Bau und der Reparatur von Radios. Und auch wenn wir heute Display-Experten sind, hängt unser Herz natürlich immer noch an der Audio-Technik, zumal der richtige Sound das perfekt eingestellte Bild erst komplett macht. 

Wissenswertes zur digitalen Audiocodierung und über bedeutsame Codecs, die nicht bzw. nicht nur zu den MPEG-Standards gehören. Im folgenden Artikel wird in diesem Zusammenhang zunächst auf ATRAC, anschließend auf AC-3 ("Dolby Digital") und zum Schluss auf AAC eingegangen.

Guter Ton gehört zum Film, wie Salz in eine Suppe. Ein Kinohit ohne entsprechend guten Soundtrack ist fast undenkbar. Um das Gefühl des "Dabeiseins" zu erzeugen ist guter Ton unverzichtbar. Im Laufe der letzten zwei Jahrzehnte wurde die Kinotontechnik auch zuhause erschwinglich. Der folgende Text zeigt Ihnen die elementaren Unterschiede zwischen den einzelnen analogen und digitalen Aufzeichnungsmethoden.

Audio Verstärker: Wieviel Leistung ist sinnvoll ?

Jeder, der einmal einen Verstärker gekauft hat, kennt das Argument vieler Verkäufer: "Nehmen Sie diesen hier - der liefert sagenhafte 1000 Watt!" Oft ist die Leistung des eigenen Verstärkers auch ein Grund, damit zu prahlen. Einige vertreten sogar die Meinung, dass ein Verstärker nur dann wirklich klingen kann, wenn die Leistung entsprechend hoch ist. Insbesondere Heimkino und Car-Hifi Anhänger geben sich in der Regel erst zufrieden, wenn sie den dicksten Amp-Boliden, der im Laden anzutreffen war, ihr Eigen nennen. Der folgende Text versucht, einmal ganz nüchtern die verschiedenen Leistungsbegriffe einzuordnen und anschließend Tipps zu geben, wie für ein vorhandenes Lautsprecherpaar ein leistungstechnisch vernünftiger Verstärker gefunden werden kann.

 

Inhaltsverzeichnis:

1. Was bedeuten die unterschiedlichen Leistungsangaben ?

2. Die Wichtigsten Messwerte 

3. Wie viel Leistung ist sinnvoll ?

 

Wie klingt es im Heimkino noch realistischer? Wie schafft man es, die Akustik eines effektgeladenen Kinofilms möglichst naturgetreu in die heimischen vier Wände zu übertragen? Vornehmlich in den höheren Preisklassen sehen die meisten Hersteller die Lösung in den Zertifizierungsstandards von THX. Doch es gibt auf der anderen Seite auch renommierte Firmen wie Yamaha, die auf die kostspielige THX-Lizensierung verzichten und auf eigens entwickelte DSP-Prozessoren für den besseren Klang setzen. Diese Einführung soll beide Methoden gegenüberstellen.

THX ist für jeden, der sich irgendwann einmal ernsthaft mit Kinotontechnik oder Heimkino befasst hat, einer der zentralen Begriffe, wenn es um qualitativ hochwertige Soundtrack-Reproduktion geht. Dabei ist THX keine neue Mehrkanaltontechnik wie Dolby Digital oder DTS, sondern ein Sammelsurium an Richtlinien, die eingehalten werden müssen, um überagende Tonqualität aus den Filmen herauszukitzeln. THX verbessert also vorhandene Übertragungstechniken für den Ton wie Dolby Surround Prologic, Dolby Digital, DTS, Mpeg-2 und andere. Doch was steckt nun tatsächlich hinter der Qualitätsnorm von Lucasfilm? Dieser Frage soll in diesem Text auf den Grund gegangen werden.

Das Heimkino wird immer populärer. Seit der digitalen Technik ist es möglich, den Kinosound auch im eigenen Wohnzimmer zu genießen. Aber welche Geräte und welche Lautsprecher sind nun erforderlich, und auf welche Eigenschaften von Geräten sollte man achten? Die Auswahl der Komponenten hängt von vielen Faktoren ab und ist sehr individuell. Die Ansprüche der Qualität, zum Beispiel beim Klang, gehen manchmal sehr weit auseinander. Deshalb kann es nicht verkehrt sein, sich vor dem Kauf schlau zu machen, bevor man nachher unzufrieden ist.

Ein Aufnahme- und Wiedergabeverfahren namens "2+2+2 Recording", welches sich besonders für die räumlich exakte Reproduktion klassischer Musik eignet, ist von der Firma MDG-Musikproduktion Dabringhaus und Grimm entwickelt worden. Hier einige Informationen dazu. 

Im ersten Teil unseres Artikels über Qualitätsmerkmale von Verstärkerschaltungen haben wir uns mit dem Thema Rauschen beschäftigt. Rauschen beeinflusst jedoch nicht alleine die Qualität der Musikwiedergabe über den Amp. Ein weiteres wichtiges Kriterium bei der Beurteilung der Güte eines Verstärkers sind Verzerrungen.

Mit der DVD Video eröffneten sich ihnen neue Dimensionen in Bild und Ton. Der verwöhnte Musikliebhaber aber wandte sich oftmals uninteressiert ab. Verbunden mit der sehr hohen Ton-Kompression bei Dolby Digital und der immer noch hohen Ton-Kompression bei DTS, waren die Ergebnisse für verwöhnte HiFi-Fans in Punkto Klangtreue und Präzision noch nicht zufriedenstellend. Nach längerem Hin und Her präsentieren die DVD-Macher den Standard DVD Audio, der die hohe Speicherkapazität der DVD neben einigen interaktiven Features wie Informationen über die Künstler oder zu den Musikstücken für reine Audio-Daten ausnutzt.

Bislang waren die Nachteile immer groß, wollte man herkömmliche Musik-CDs in Surround-Klangqualität genießen: Besonders bei Dolby ProLogic war das Klangbild mittenbetont, der Bass war drastisch schwächer als bei der Stereowiedergabe, die klangliche Präzision war ebenfalls nicht mehr sehr hoch. Zu viele Klanganteile kamen aus dem Center-Lautsprecher, Regelmöglichkeiten gab es nur in sofern, den Center via „Phantom Mode“ gleich ganz auszuschalten.

Wer akustisch mehr als den inzwischen bei Heimkino-Fans sehr weit verbreiteten 5.1-Klang in Dolby Digital und DTS in seinem Heimkino realisieren möchte, sollte sich mit dem Thema Extended Surround-Tonformate beschäftigen. Dieses Special soll erklären, wie genau die 6.1-Formate funktionieren und inwieweit sich diese auch mit herkömmlichen 5.1-Systemen vertragen.

Die Audio-Compact Disc wurde im Laufe der 1970er Jahre unter Federführung der Firmen Philips und Sony entwickelt. Die ersten Hardware Prototypen konnte Philips 1979 in Europa vorstellen, ein Jahr später im Juni 1980 gaben Sony und Philips ihren neuen CD-Standard offiziell bekannt.

Seit Einführung der Audio Compact Disc (CD) und dem Aufkommen des Digital Audio Tapes (DAT) hat sich im Audiobereich digitale Technik zunehmend durchgesetzt. Als grundlegendes Digitalisierungsverfahren verwenden sowohl die CD als auch DAT die Pulse Code Modulation (PCM). Diese Technik übersetzt das analoge Originaltonsignal über Sampling, Quantisierung und Codierung in die digitale Welt. Da PCM keine Datenreduktion verwendet, erreicht man hervorragende Klangqualität - allerdings wird sie mit hohem Speicherbedarf erkauft. Auf eine CD passen in PCM maximal 80 Minuten an Audiodaten.

Die HiFi- und Heimkinotechnik unserer Tage wurde erst durch eine bahnbrechende Innovation möglich: Über die Umwandlung von Schall in elektrische Energie. Diese Aufgabe übernimmt das Mikrofon, während der Lautsprecher die umgekehrte Wandlung vornimmt: Er sorgt dafür, dass die elektrischen Schwingungen wieder in Schallwellen umgewandelt werden - somit ist er das letzte Glied der Heimkino- oder Stereoanlage, welches den im Endeffekt vom Zuhörer gehörten Klang zusammen mit der Akustik des Hörraums am stärksten beeinflussen kann. 

Der Lautsprecherkauf und die Aufstellung sowie Einpegelung der Surround-Anlage sind nicht unbedingt einfach und für jedermann ohne jegliches Vorwissen zu bewältigen. Die Lautsprecher spielen zusammen mit den akustischen Eigenschaften des Hörraums und der richtigen Handhabung der Surround-Anlage eine wesentliche Rolle bei der Erzielung eines optimalen Hörerlebnisses. Wir wollen einige Grundlagen erläutern, damit der Lautsprecherkauf und das Verständnis der technischen Basics ein wenig einfacher wird.

Jeder, der sich eine Heimkino-Anlage installieren oder sein bestehendes System updaten möchte, steht beim Kauf neuer Komponenten vor keiner leichten Entscheidung. Das betrifft sowohl den DVD-Player als auch den AV-Verstärker oder AV-Receiver als Zentrum der Heimkino-Anlage. Dieses kleine Special befasst sich mit den wichtigen Merkmalen von AV-Verstärkern und -Receivern.

Während wir uns im dritten Teil unserer Reihe zur Raumakustik um die Optimierung im tiefen Frequenzbereich gekümmert haben, werden wir uns im vorliegenden vierten Teil mit der Verbesserung der akustischen Bedingungen des Hörraumes im mittleren und hohen Frequenzbereich ab ca. 200Hz beschäftigen. Hier werden wir vor allem Tipps zur Verbesserung der Nachhallzeit geben, mit deren Hilfe zu hallige Räume klanglich stark verbessert werden können. Reflexionen werden auch in diesem Artikel wie im ersten Teil unserer Reihe über Raumakustik Mittelpunkt stehen.

 

Inhaltsverzeichnis:

1. Optimierung der Raumakustik
2. Optimierung der Nachhallzeit mit gewöhnlichen Mitteln
3. Optimierung der Nachhallzeit mit professionellen Mitteln
4. Optimierung der Aufstellung der Lautsprecher
5. Zusammenfassung

 

1. Optimierung der Raumakustik


Im ersten Teil unserer Artikelreihe haben wir erläutert, dass auf jedem Tonträger indirekter Schall vorhanden ist, nämlich der des Raumes, in dem die Produktion abgemischt wurde (bei Unterhaltungsmusik auch immer öfter künstlich erzeugter Hall). Für eine naturgetreue Wiedergabe sollte unser Hörraum daher diese konservierte Raumakustik möglichst wenig verändern. Perfekt wäre eine sehr geringe Nachhallzeit nahe null Sekunden. Dann würde störender Nachhall komplett entfallen. Leider wird sich der Einfluss unseres Raumes nie völlig abschalten lassen. Dies wäre ansatzweise nur dann möglich, wenn unser Raum so wie professionell genutzte reflexionsarme Räume konstruiert und optimiert wäre. Das Bild rechts zeigt einen solchen Raum, der bei der Firma Visaton zu Messzwecken bei der Konstruktion von Lautsprechern verwendet wird. Anhand des Bildes erkennt man schon, dass eine derartige Optimierung für das heimische Wohnzimmer nicht möglich ist. Das Zimmer wäre absolut nicht mehr alltagstauglich, außerdem bliebe die Behaglichkeit auf der Strecke.

Wir werden Reflexionen in unserem Hörraum also wohl kaum perfekt eliminieren können, was aber auch gar nicht nötig ist. Bereits einige alltagstaugliche Veränderungen können akustisch Wunder wirken. In den folgenden Abschnitten werden wir Ihnen einige klangverbessernde Tipps geben. Wichtig in diesem Zusammenhang ist zunächst die Tabelle aus unserem ersten Artikel, in der der Absorptionsgrad einiger Materialien aufgelistet ist. Aufgrund ihres sehr geringen Absorptionsgrades sind glatte harte Flächen, wie Glasscheiben, Steinwände oder Parkettböden als ungünstig einzustufen. Vielleicht erkennen Sie Ihr Wohnzimmer jetzt wieder. Schließlich wird gerade hier häufig Parkettboden verwendet, es sind große Fensterflächen vorhanden, um viel Licht in den Raum zu lassen, und die Wände bestehen nun mal in der Regel aus einer Steinwand mit Anstrich. Viele Wohnzimmer sind also von der Materialzusammensetzung her nicht gerade akustisch optimiert.

Sie müssen aber Ihren Parkettboden nicht gleich herausreißen und Ihre Fenster zumauern. Es gibt einige einfache Tricks diese ungünstigen Materialien zu kompensieren. Der folgende Abschnitt soll Ihnen die Auswahl von Materialien erleichtern. Zunächst betrachten wir anhand eines Beispiels die Optimierung mit gewöhnlichen Mitteln. Im Anschluss möchten wir Ihnen noch einige professionelle Hilfsmittel vorstellen.

 

2. Optimierung der Nachhallzeit mit gewöhnlichen Mitteln

Wir betrachten einen Raum mit der Länge L = 5m, der Breite B = 3m und der Höhe H = 2,5m.Wände und Decke bestehen aus Steinwand mit Anstrich, der Boden ist mit Parkett belegt. Außerdem befinde sich eine Holztür mit der Breite BT = 0,8m und Höhe HT = 2m in einer der Wände mit 3m Breite. In der Längswand der Breite 5m ist ein großes Glasfenster mit den Abmessungen Breite BF = 3m und Höhe HF = 1,5m eingelassen. Die einzelnen Materialflächen berechnen sich mit diesen Angaben zu:



Daraus können wir mit Hilfe der Formel für die Nachhallzeit und den Werten der Absorptionsgrade dieser Flächen aus dem ersten Artikel unserer Reihe die Nachhallzeit dieses Raumes bestimmen:



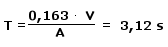
Bisher ist die Nachhallzeit katastrophal schlecht, wie bei diesen Materialien auch erwartet. Was können wir zur Verbesserung tun? Wir betrachten die Formel für die Nachhallzeit. Die einzige Variable, die wir ändern können ist die totale Absorption A. Das Volumen V des Raumes ist schließlich mit den Raumabmessungen fest vorgegeben. Die totale Absorption berechnet sich nach



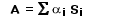
aus der Summe aller Einzelflächen multipliziert mit ihrem jeweiligen Absorptionsgrad α. Aus diesem Grund wird die totale Absorption größer, wenn die Anzahl der Flächen mit großem α steigt. Entsprechend wird sie kleiner, wenn viele schallharte glatte Flächen mit niedrigem α vorhanden sind. Der entscheidende Weg zur Verbesserung (also Erniedrigung) der Nachhallzeit ist die Erhöhung der totalen Absorption - denn diese steht in der Formel für T im Nenner des Bruches, wodurch T kleiner wird, wenn A ansteigt.

Ganz allgemein erreichen wir also eine Verbesserung der Raumakustik im mittleren und hohen Frequenzbereich, indem wir möglichst viele schallharte Stoffe durch poröse, weiche Materialien ersetzen. Unter poröse Materialien fallen dabei alle fasrigen, flauschigen und weichen Stoffe, wie beispielsweise Teppiche, Vorhänge und Polstermöbel. Sie entziehen der durchlaufenden Schallwelle Energie durch Reibung der sich bewegenden Luftmoleküle an den feinen Fasern des Materials. Diese Energie wird in Wärme umgesetzt. Da sich die Luftmoleküle umso schneller bewegen, je höher die Frequenz des Schalls ist, nimmt die absorbierende Wirkung der Materialien mit steigender Frequenz stark zu. Tiefe Frequenzen hingegen lassen sich kaum durch diese Materialien beeindrucken, aber für die Verringerung dieser Wellen haben wir Ihnen ja bereits im dritten Teil unserer Raumakustikreihe Tipps an die Hand gegeben. Stoffe, die schallschluckende Eigenschaften aufweisen werden auch als Schluckstoffe bezeichnet.

Wir wollen uns nun anhand unserer Beispielrechnung ansehen, wie gut sich mit einigen Mitteln die Nachhallzeit des Raumes verbessern lässt. Dazu belegen wir das Parkett teilweise mit einem Teppich der Abmessungen 4m x 2m. Vor das Fenster kann wenn Musik gehört werden will ab sofort ein schwerer Vorhang gehängt werden. Dieser hat die Abmessungen 4m x 2,5m, wodurch er gleich auch noch einen Teil der Wand mit verdeckt. Die Wände selbst werden kurzerhand mit dicker Tapete tapeziert. Als Materialflächen in unserem Hörraum ergeben sich jetzt die folgenden Werte:



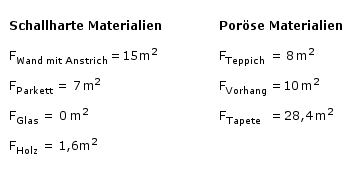
Mit Hilfe der jeweiligen Werte für α können wir die neue Nachhallzeit berechnen. Diese beträgt jetzt:



Die Nachhallzeit ist also fast sechs mal kleiner, als im Raum mit den zuerst verwendeten Materialien. Sie ist bereits in einen Bereich gefallen, der akzeptable akustische Ergebnisse erwarten lässt. Die DIN-Norm empfiehlt für die Hifiwiedergabe in Wohnräumen Nachhallzeiten zwischen etwa 0,2 und 0,5 Sekunden. Die genaue Empfehlung kann aus der folgenden Zeichnung abgelesen werden. Beachten Sie vor allem, dass in dieser Empfehlung die Frequenzabhängigkeit der Nachhallzeit mit berücksichtigt wurde.
 

 

 

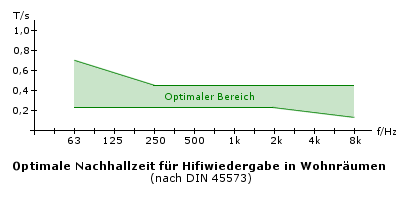
Für optimale Musikwiedergabe sollte der Wert also noch etwas weiter sinken. Das erreichen Sie sehr leicht, indem Sie zum Beispiel eine Sofaecke in den Raum stellen. Auch jede Person, die sich im Raum aufhält, wird, wie in unserem ersten Artikel bereits bemerkt, die Nachhallzeit weiter verkürzen. Variieren Sie vor allem auch die Position der Einrichtungsgegenstände im Raum. Diese wird in unseren bisherigen Berechnungen leider nicht berücksichtigt, kann aber großen Einfluss auf die Nachhallzeit und damit die Akustik des Raumes ausüben. Es lassen sich also bereits durch geschickte Wahl der Einrichtung gute akustische Ergebnisse erzielen. Für perfekte Optimierungen genügt dieses Vorgehen allein natürlich noch nicht. Dem Raumakustiker stehen für die Verbesserung eines Raumes daher einige Hilfsmittel zu Verfügung. Einige davon sollen im nächsten Abschnitt vorgestellt werden. Sollte Ihnen Ihr Hörraum zu hallig erscheinen, so könnten diese Spezialmittel das richtige sein, um diese Tatsache zu ändern.

 

3. Optimierung der Nachhallzeit mit professionellen Mitteln

Zusätzlich zur Optimierung mit gewöhnlichen Mitteln kann in besonders widerspenstigen Hörräumen die Nachhallzeit mit Hilfe von professionellen Mitteln eingestellt werden. In erster Linie sind hier Absorberkonstruktionen zu nennen. Zu dieser Gattung gehören übrigens auch die im dritten Teil unserer Reihe über Raumakustik besprochenen Helmholtz-Resonatoren und Plattenschwinger. Diese arbeiten im tiefen Frequenzbereich. Wir wollen uns im folgenden nun Absorber für den mittleren und vor allem hohen Frequenzbereich ansehen. Man spricht hier auch allgemein von Höhenabsorbern.

Höhenabsorber wirken im Prinzip genauso wie ein Vorhang oder Polstermöbel.Am weitesten verbreitet sind sogenannte Akustikplatten, wie im Bild links gezeigt (Firma Heraklith). Diese bestehen aus einer speziellen Materialzusammensetzung (z.B. magnesitgebundene Holzwolle, Steinwolle), deren α zumindest für hohe Frequenzen praktisch gleich 1 ist. Es handelt sich also um praktisch perfekte Schallschlucker. Akustikplatten können bequem an jeder Wand befestigt werden.

Insbesondere bei der Wandanbringung ergibt sich allerdings ein Problem. In der Nähe der Wand ist die Geschwindigkeit, mit der sich die durch den Schall angeregten Luftmoleküle bewegen sehr gering. Schluckstoffe, aus denen Akustikplatten bestehen, wirken jedoch nur dann, wenn die Luftbewegung möglichst hoch ist. Die folgende Skizze verdeutlicht den Sachverhalt:

 

 

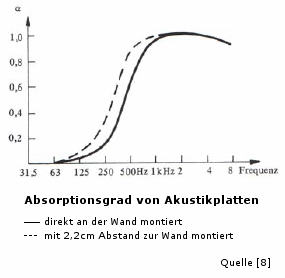
Man erkennt, dass die absorbierende Wirkung bei steigendem Wandabstand insbesondere im Bereich mittlerer Frequenzen deutlich zunimmt. Sollen also neben den hohen Frequenzen auch mittlere Frequenzen unterhalb von etwa 1kHz absorbiert werden, so müssen die Platten auf einem Gerüst montiert werden, um den erforderlichen Wandabstand einzuhalten. Die gesamte Absorberdicke hat selbstverständlich ebenfalls großen Einfluss auf die dämpfende Wirkung. Die minimale Dicke d des Absorbers zur Dämpfung von Schall der Wellenlänge λ ist über den recht einfachen Zusammenhang d = λ/4 gegeben.

Die Materialien, aus denen Akustikplatten bestehen, werden auch für eine weitere Absorberart verwendet, die sogenannten Schlitz- oder Lochplattenabsorber (siehe Bild rechts). Diese werden ebenfalls an der Wand befestigt und besitzen einen schichtartigen Aufbau. Die äußere sichtbare Schicht besteht aus einer mehr oder weniger stark gelochten Holzplatte. Dieser Schicht schließt sich ein stark dämpfender, bis etwa 5cm dicker Bereich aus Schluckstoffen an. Schlitz- und Lochplattenabsorber werden vor allem zur Bekämpfung zu langer Nachhallzeiten im mittleren Tonbereich verwendet und reichen bei geschickter Konstruktion auch ein Stück in den Tieftonbereich hinab. Ähnlich wie bei den Akustikplatten ist die Absorptionswirkung abhängig von der Montageentfernung zur Wand. Lässt man einen gewissen Wandabstand zu, so verbessert sich die Absorberwirkung zu tiefen Frequenzen hin.

 

4. Optimierung der Aufstellung der Lautsprecher

Natürlich ist die Nachhallzeit nicht das einzige Kriterium, das bei der Optimierung eines Hörraumes für Hifiwiedergabe berücksichtigt werden muss. Mindestens genauso wichtig ist die korrekte Position der Lautsprecher und der Hörposition. Hierauf sind wir im dritten Teil unserer Raumakustikreihe hier eingegangen, allerdings nur für tiefe Frequenzen. Während im Bassbereich Hör- und Lautsprecherposition weitestgehend unabhängig voneinander sind, da das Ohr tiefe Frequenzen nicht im Raum lokalisieren kann, muss bei der Optimierung im mittleren und hohen Frequenzbereich die Stereowirkung der Lautsprecher berücksichtigt werden. Diese kann sich nur dann optimal ausbilden, wenn der Zuhörer von beiden Speakern gleich weit entfernt ist. Eine optimale geometrische Anordnung von Lautsprechern und Sitzposition kann mit Hilfe des bekannten Stereodreiecks herausgefunden werden. Die folgende Skizze veranschaulicht das.

 

 

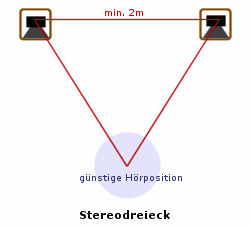
Die Lautsprecher sollten dabei nach Möglichkeit mindestens 2 Meter auseinander stehen, da die Stereowirkung sonst sehr eng und unrealistisch erscheint. Die Sitzposition sollte sich möglichst auf der Mittelsenkrechte auf der die Lautsprecher verbindenden Dreiecksseite befinden, da das Stereoklangbild sonst links- oder rechtslastig wird. Der Abstand zur Lautsprecherebene darf nicht zu klein gewählt werden, da die imaginären Schallquellen der Darbietung sonst zunehmend ähnlich wie beim Kopfhörer im Kopf und nicht vor einem lokalisiert werden.

Auch das andere Extrem einer sehr weit von den Boxen entfernten Hörposition kann auf keinen Fall empfohlen werden. Der Grund hierfür liegt darin, dass der Direktschallanteil mit dem Abstand zu den Schallquellen stark abfällt. Wie wir im ersten Artikel unserer Reihe erläutert haben, steigt dagegen der Anteil des Diffusschalls am Gesamtschall mit zunehmendem Abstand stark an. Je weiter man sich von den Boxen entfernt, desto mehr verwischt daher die räumliche Abbildung der imaginären Quellen zwischen den Speakern.

Bisher wurde die Aufstellung nur nach geometrischen Kriterien optimiert. Bezieht man den Hörraum mit seinen akustischen Eigenheiten mit in diese Überlegungen ein, so wird die Sache etwas komplizierter. Die Lautsprecher werden unweigerlich einen Teil ihres Schalls in Richtung der umgebenden Raumwände abstrahlen. Werden diese Schallwellen an den Wänden unterschiedlich stark reflektiert bzw. absorbiert, was bei sich stark unterscheidendem Wandmaterial der Fall ist, so gelangen vom einen Lautsprecher mehr Reflexionen als vom anderen an der Hörposition an. Genau das gleiche ist der Fall, wenn die Speaker nicht den gleichen Abstand zu den umgebenden Wänden besitzen. Besonders ungünstig ist beispielsweise die Aufstellung des linken Lautsprechers mit 50cm Abstand zu einer großen Glasfläche und die Positionierung des rechten Lautsprechers im Abstand von zwei Metern neben einen Wandteppich. Aufgrund des sehr geringen Absorptionsgrades der Glasfläche gegenüber dem Wandteppich und des unterschiedlichen Abstandes zu den Begrenzungsflächen besitzen die nach Reflexion zum Hörer gelangenden Schallwellen des linken Speakers wesentlich höhere Intensität, als die Wellen des rechten Speakers. Die linke Box erscheint dem Gehör daher lauter und schon verschiebt sich die Stereoabbildung wieder. Optimal wäre es also das Wandmaterial im Bereich beider Speaker identisch zu wählen und auch den Abstand der Lautsprecher zu den Wänden möglichst gleich zu gestalten.

Verwendet man allerdings gut reflektierende Wandmaterialien, wie zum Beispiel eine Steinwand mit Anstrich oder eine Holzvertäfelung, so schafft man zwar identische Abstrahlverhältnisse für beide Lautsprecher, handelt sich aber mit hoher Wahrscheinlichkeit Flatterechos aufgrund der parallelen Wände ein. Flatterechos sind bekannt für ihre stark klangverschlechternde Wirkung. Die Präzision der Wiedergabe wird deutlich herabgesetzt. Besser wäre es die Lautsprecherebene nicht parallel zu den Wänden, sondern wie auf dem folgenden Bild im Raum zu positionieren:

 

 

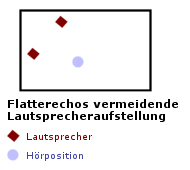
So werden zumindest die durch parallele Raumseitenwände entstehenden Flatterechos vermieden. Leider ist die Abstrahlumgebung für diesen Fall wieder nicht ganz identisch für beide Speaker und es können nach wie vor Flatterechos zwischen Decke und Boden auftreten. Außerdem ist diese Aufstellungsvariante bei weitem nicht in jedem Wohnzimmer möglich. Werden die Lautsprecher also konventionell entlang einer Raumseite aufgestellt, so sollte das Wandmaterial zumindest möglichst rau und absorbierend sein. Absorbierend deshalb, weil dann eventuell entstehende Flatterechos durch hohen Energieverlust bei der Reflexion schnell abklingen. Raues oder stark zerklüftetes Material sorgt dafür, dass Schallwellen ab einer bestimmten Grenzfrequenz die parallelen Wände nicht "sehen". Sie werden wie im ersten Artikel erläutert von den einzelnen Vertiefungen und Überhöhungen in unterschiedliche Richtungen reflektiert und damit in den Raum zurückgestreut. Leider funktioniert das bei einer normalen Rauheit wie beispielsweise Rauputz nur für hohe Frequenzen. Mittlere und tiefe Frequenzen werden nicht gestreut. Im professionellen Bereich verwendet man aus diesem Grund spezielle Diffusoren. Diese bestehen aus einer unregelmäßig angeordneten Ansammlung von Einzelflächen verschiedener Größe. Aufgrund der recht großen Abmessungen der Einzelflächen können Diffusoren bis in den Tieftonbereich hinein wirken. Leider sind die Konstruktionen nicht sehr augenfällig und passen schlecht zur heimischen Wohnzimmereinrichtung, wie auf dem Bild rechts zu sehen ist. Gezeigt ist ein kleines Musikstudio mit Diffusoren an Rückwand und Decke (Quelle [5]).

Doch es müssen nicht spezielle Diffusoren sein, auch mit der unregelmäßigen Anordnung von Gegenständen im Hörraum können Sie Flatterechos vermeiden. In diesem Zusammenhang sind beispielsweise Dachräume aufgrund der Dachschräge und den damit nur teilweise parallelen Wänden hervorragend als Hörräume geeignet. Stehen nur Räume mit parallelen Wänden zur Verfügung, so können eventuell aufstellbare Trennwände Wunder vollbringen.

 

5. Zusammenfassung

Abschließend möchten wir Ihnen zusammenfassend kurz den Weg skizzieren, den Sie am sinnvollsten bei der Optimierung Ihres Hörraumes gehen sollten.

  • Führen Sie zunächst sofern nötig bauliche Maßnahmen wie Tapezieren der Wände durch
  • Anschließend sollten Sie bestimmen, an welchem Ort Geräte, Lautsprecher und Zuhörer ihren Platz finden sollen. Beachten Sie dabei unsere Positionierungstipps für alle Frequenzen.
  • Sind die Positionen festgelegt, so können Sie falls nötig die Nachhallzeit noch mit Hilfe von Teppichen, Polstermöbeln und ähnlichem verbessern. Achten Sie aber unbedingt darauf, dass die Abstrahlverhältnisse auch nach dieser Optimierung für linke und rechte Box möglichst gleich sind!
  • Ganz zum Schluss können Sie noch störende Raumresonanzen mit Hilfe von Helmholtz-Resonatoren ausmerzen. Achten Sie auch hier wieder darauf, dass Sie die Abstrahlbedingungen für linken und rechten Lautsprecher möglichst nicht mehr bzw. in gleicher Weise ändern!

Quellenangaben:

  1. Handbuch der Elektroakustik; Günther Boye, Urbi F. Herrmann; Hüthig Buch Verlag Heidelberg; ISBN:3-7785-1575-6
  2. TMR Audio
  3. Dokument zur 5. Internationalen Internet- und Multimedia-Tagung (Zürich, 24.10.2002); "Raumakustik und Multimedia"; Autor: Kurt Eggenschwiler
  4. www.sengpielaudio.com
  5. EMPA/HSR-Tagung 2001; "Holz in der Raumakustik"; Autor: Kurt Eggenschwiler
  6. Klang - Musik mit den Ohren der Physik; John R.Pierce; Spektrum der Wissenschaft
  7. Audio Consequent
  8. Referat über Raumakustik

Computerprogramme zur Simulation der Raumakustik

  1. Programm von TMR-Audio
  2. CARA - Computer Aided Room Acoustics

 

Raumakustik 3 - Der Hörraum bei tiefen Frequenzen

Während wir uns in unseren ersten beiden Teilen zur Raumakustik mit den Grundbegriffen beschäftigt haben, geht es jetzt im dritten und vierten Teil in die Praxis. In den folgenden Abschnitten sollen Ihnen Wege und Möglichkeiten aufgezeigt, sowie Tipps und Tricks gegeben werden,ihren heimischen Hörraum akustisch zu optimieren. Im dritten Teil steht dabei die Optimierung im Bereich tiefer Frequenzen im Vordergrund, während sich der vierte Teil mit der Optimierung im mittleren und hohen Frequenzbereich beschäftigt. Wir möchten ausdrücklich betonen, dass die Optimierung von kleinen Abhörräumen für Hifimusikwiedergabe im Vordergrund steht.Möchten Sie mittlere und große Säle für Theater, Konzerte oder Sprachveranstaltungen akustisch verbessern, so ist dieser Artikel sicher nicht das richtige für Sie, da Sie in diesen Fällen andere Optimierungsschwerpunkte setzen müssen. In diesem Fall können wir Ihnen das Studium der Quellen [1], [3] und [5] empfehlen.

 

Inhaltsverzeichnis

1. Optimale Raumproportionen
2. Optimierte Aufstellung von Lautsprechern und Geräten im Bezug auf stehende Wellen
3. Verminderung der Eigenmoden durch Helmholtz-Resonatoren
4. Verbesserung der Nachhallzeit im Tieftonbereich: Plattenschwinger

 

1. Optimale Raumproportionen:

Die Optimierung des Hörraumes fängt bei der Wahl des geeigneten Raumes im Haus an. Leider ist diese Wahl meist nur äußerst begrenzt möglich, schließlich werden die Räume in der Regel bereits genutzt. Insbesondere bei kleinem Hörraum, wie das heimische Wohnzimmer, ist der Einfluss der geometrischen Zimmerabmessungen auf stehende Wellen nicht zu vernachlässigen. Gute akustische Vorraussetzungen im Bezug auf Eigenmoden bringen nur die Räume mit, deren Raumabmessungen sich nicht ohne Rest durcheinander teilen lassen. Ganzzahlige Raumabmessungen (Länge, Breite, Höhe) begünstigen stehende Wellen. Es kommt dann zu einem wie in unserem zweiten Artikel angedeutet äußerst ungünstigen Zusammenfall der Resonanzfrequenzen verschiedener Ordnung. Ungünstig ist daher zum Beispiel ein Raum mit 3m Höhe, 6m Breite und 12m Länge. Als akustisch günstig haben sich dagegen Räume herausgestellt, deren Wände krumme Längenwerte aufweisen. Ein Beispiel für ein günstiges Längenverhältnis zeigt folgende Tabelle:
 

HöheBreiteLänge
1 1,87 2,73

 

Beispiel:
Ein Raum habe die Höhe H = 2,5m.
Die optimale Breite hierzu wäre nach obigen Beispielwerten: B = 1,87 * 2,5m = 4,675m
Für die Länge ergäbe sich: L = 2,73 * 2,5m = 6,825m

Der Einfluss der Raumgeometrie wird übrigens umso kleiner, je größer der Raum wird. Daher werden heute in erster Linie kleine Tonstudios und Abhörraume geometrisch optimiert gebaut. Große Säle hingegen weisen keine so große Problematik im Bezug auf stehende Wellen auf, da hier die Abmessungen so groß sind, dass stehende Wellen in sehr tiefen, nicht mehr hörbaren Bassregionen auftreten und damit das Klangbild nur wenig stören.

 

2. Optimierte Aufstellung von Lautsprechern und Geräten im Bezug auf stehende Wellen

Der erste Schritt nach der Wahl des Raumes betrifft die Festlegung wo im Raum Geräterack und Lautsprecher zu finden sein sollen. Wir betrachten in diesem Abschnitt die im Bezug auf stehende Wellen perfektionierte Positionierung. Optimierungsvorschläge für den mittleren und hohen Tonbereich finden Sie im vierten Teil unserer Reihe über Raumakustik.

Nun müssen wir herausfinden, welche Raumresonanzen unser Hörraum aufweist und wie Maxima und Minima in der Basswiedergabe im Raum verteilt sind. Ist Ihr Hörraum quaderförmig strukturiert, so können Sie die Resonanzen mit den Formeln aus unserem zweiten Artikel, den Sie ebenfalls hier auf http://www.burosch.de finden, berechnen. Hierzu auch nochmals der Hinweis auf das Online-Berechnungstool, mit dem Sie sich einige Tipparbeit mit Ihrem Taschenrechner ersparen. Genauer ist sicher die Verwendung eines speziellen Raumakustiksimulationsprogramms. Beispiele finden Sie wie immer unten in den Quellenangaben.

Unsere Professional-CD

Es gibt auch noch eine dritte Möglichkeit, die ebenfalls zu sehr brauchbaren Ergebnissen führt, da sie weder auf Berechnung, noch auf Simulation der Raumakustik beruht, sondern eine ungefähre Ortung der in Ihrem Hörraum tatsächlich vorhandenen Maxima und Minima ermöglicht. Hierzu benötigen Sie eine gute Audio-Test-CD (zum Beispiel unsere Professional Audio-CD, die Sie im Shop hier auf

http://www.burosch.de

finden). Positionieren Sie Ihre Lautsprecher im Raum und spielen Sie von dieser CD ein Sinussignal im Bereich von 20Hz bis 200Hz ab. Beispiele wären hier die Tracks 9 bis 19 der zweiten CD unserer Professional Audio-CD. Während das Signal läuft gehen Sie im Raum auf und ab. Sie werden dabei Pegelveränderungen des Signals bemerken. An Orten, an denen das Signal laut erscheint, sind Bäuche der Eigenmoden des Raumes zu finden, während ein fast verschwindendes Signal auf einen Knoten hinweist. Sinnvollerweise markieren Sie die gefundenen Knoten und Bäuche in einem Plan Ihres Raumes, eventuell auf Millimeterpapier. Besonders genau wird Ihre Messung selbstverständlich, wenn Sie mit Hilfe eines Schalldruckmessgerätes Ihren Raum ausmessen. Der Vorteil der Messmethode gegenüber den obigen Methoden liegt darin, dass Sie die tatsächlichen akustischen Bedingungen in Ihrem Hörraum genauestens bestimmen können. Sowohl die Rechnung, als auch die Computersimulation werden Ihnen immer nur die wahrscheinlichsten akustischen Bedingungen liefern. Wenn Sie bedenken, dass jeder Sessel, jeder Tisch und Schrank und überhaupt alles, was Sie in den Raum einbringen die Akustik verändert, so erscheint die Messmethode tatsächlich am sinnvollsten.

Zunächst betrachten wir die Aufstellung des Geräteracks. Man könnte meinen, dass die Position der Geräte relativ egal sein sollte, sie ist es aber bei weitem nicht. Es wird grundsätzlich so sein, dass der Schall der Lautsprecher die einzelnen Elektronikkomponenten zu Schwingungen anregt. Diese Vibrationen klingen in den einzelnen Bauteilen (Widerstände, Kondensatoren, Halbleiter und andere) verzögert wieder ab. Dieser Effekt wird übrigens auch als Mikrophonie bezeichnet. Es handelt sich also um eine Rückkopplung der Schallwellen auf die Geräteelektronik. Warum ist dieses Schwingen so problematisch? Diese Schwingung der Bauteile bewirkt, dass die rückgekoppelte Schwingung auf das gerade in Verstärker, CD-Player und anderen Komponenten verarbeitete Signal aufmoduliert wird. Mit anderen Worten die Schwingungen führen zu einer Veränderung der Amplitude und Phase des Musiksignals. Es kommt zu dynamischen Verzerrungen. Das diese Wirkung den guten Klang nicht gerade fördert sollte jedem klar sein.

 

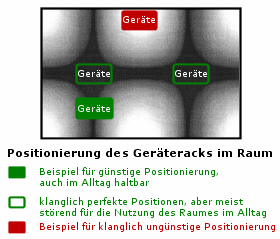
Positionierung des GerÀteracks im Hörraum

 

Was wir benötigen ist also eine möglichst schallruhige Position. Optimal wäre die Platzierung der Elektronik in einem anderen Raum abseits der Lautsprecher. Aber wer will schon bei jedem CD- oder DVD-Wechsel den Raum verlassen. Auch innerhalb des Hörraumes lassen sich Orte finden, die für das Geräterack besser geeignet sind als andere. Dazu betrachten wir unser Bild der stehenden Wellen. Perfekt wäre die Platzierung der Elektronik in einem Knoten (im Bild schwarzer Bereich). Dadurch werden tieffrequente Störstrahlungen schon einmal drastisch herabgesetzt. Dummerweise liegen die ausgeprägtesten Knoten bei praktisch jedem quaderförmigen Raum in der Raummitte, die verständlicherweise eher ungünstig für die Aufstellung der Hifianlage ist. Nicht nur, weil die Verlegung der Zuleitungskabel kompliziert wird, sondern auch weil die Anlage im Alltag ständig im Weg steht, sofern der Raum auch für andere Dinge, als für Musikwiedergabe genutzt wird. Eine Platzierung direkt an der Wand verbietet sich leider aufgrund der dort sehr intensiven Bäuche der Eigenmoden. Am sinnvollsten erscheint eine Aufstellung mit einigem Abstand, zum Beispiel von 50cm, zur Raumwand. Vermeiden sollten Sie in jedem Fall die Positionierung im Schallfeld der Lautsprecher. Auch Orte zwischen den Speakern sind nur bedingt geeignet. Wenn überhaupt, dann mit etwas Versatz der Geräte nach hinten.

Wenden wir uns nun der Bestimmung der Lautsprecherstandorte zu. Hier lässt sich sicher einiges experimentieren. Wir wollen Ihnen einige Tipps an die Hand geben, wie Sie relativ schnell eine günstige Position für Ihre Speaker finden. Anders als die Elektronik spielen bei der Aufstellung der Boxen nicht nur stehende Wellen eine Rolle, sondern auch Reflexionen im mittleren und hohen Frequenzbereich. Zunächst wollen wir aber wieder nur den Einfluss stehender Wellen betrachten. Der obere Tonbereich folgt dann im vierten Teil unserer Reihe hier auf

http://www.burosch.de

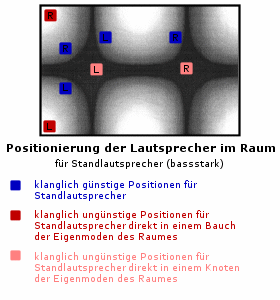
Anders als bei der Bestimmung des optimalen Aufenthaltsortes der Elektronik hängt der perfekte Platz Ihrer Lautsprecher von den qualitativen Eigenschaften Ihrer Speaker im Bassbereich ab. Besitzen Sie großvolumige Standlautsprecher, so werden Sie vermutlich bei der Positionswahl von Bereichen ausgeprägter Wellenbäuche abweichen müssen. Der Grund hierfür ist ganz klar. Standlautsprecher besitzen in der Regel einen voluminösen Tiefbassbereich. Stellen Sie so einen Schallwandler in den Bereich eines Maximums der Raummoden, so wird der Bassbereich garantiert aufgedickt und Sie erhalten ein zum Dröhnen neigendes im Bassbereich wenig differenziertes Klangbild. Bassstarke Lautsprecherkonstruktionen gehören daher mit einigem Abstand zur Wand aufgestellt. Hier ist das Maximum der Eigenmoden bereits überwunden. Extrem bassstarke Lautsprecher können auch in den näheren Bereich von Knoten gestellt werden. Allerdings scheidet dieser Aufstellungsort in der Regel dann aus, wenn der Raum auch für den Alltag tauglich sein soll.

 

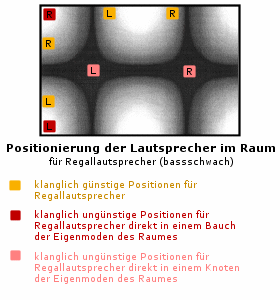Positionierung von Standlautsprechern   Positionierung von Regallautsprechern

 

Wie Sie bassschwache Lautsprecher, wie kleine Regalboxen oder ähnliches, positionieren müssen, sollte jetzt natürlich klar sein. Diese werden logischerweise nah an die Wand gestellt. Hier wird der Bassbereich der Böxchen zusätzlich durch die Eigenmoden des Raumes verstärkt, was zu einem voluminöseren, wärmeren Klangeindruck führt. Vor Extremen soll allerdings gewarnt werden. Eine Aufstellung der Lautsprecher direkt in einen Knoten oder einen Bauch der Eigenmoden führt nur in den seltensten Fällen zu guten Ergebnissen. Meist kommt es in einem ausgeprägten Knoten zu einer zu starken Abschwächung des Bassbereiches, was zu dünnem kühlem Klang führt, in einem Bauch werden einzelne Bassfrequenzen (die Resonanzfrequenzen des Raumes) dagegen gleich so stark betont, dass das Klangbild auch bei kleinen Boxen zum dröhnen neigt.

 

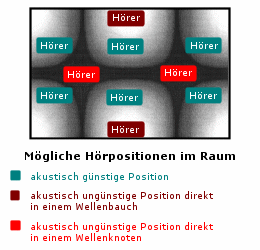
Mögliche Hörpositionen im Raum

 

Nun zur Frage wo Sie Ihren Sessel zum Musikhören hinstellen sollten. Die perfekte Hörposition hängt im Tieftonbereich ähnlich von den Raumresonanzen ab, wie die Position der Lautsprecher. Vermeiden sollten Sie in jedem Fall einen Sitzplatz in einem ausgeprägten Knoten. Sie werden dann mit an Sicherheit grenzender Wahrscheinlichkeit von der Basswiedergabe Ihrer Speaker nicht viel mitbekommen. Leider scheidet dadurch die Raummitte schon einmal aus. Auch wandnahe Hörpositionen, wie Sie häufig günstig währen, sind leider nicht das Optimum. Hier finden sich, wie Sie mittlerweile wissen, ausgeprägte Maxima in der Basswiedergabe. Daher kommt Ihnen der Bassbereich Ihrer Lautsprecher in so einer Sitzposition wahrscheinlich als dumpf, verhangen und dröhnend vor. Eine perfekte Hörposition ergäbe sich etwas von der Wand entfernt mit einem halben bis einem Meter Wandabstand. Diese Position ist natürlich im normal genutzten Wohnzimmer meist nicht sehr günstig.

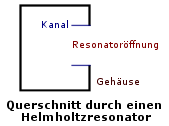
Kommt es an Ihrem Hörort trotz optimierter Aufstellung zu ausgeprägten Resonanzen bei bestimmten Bassfrequenzen, erkennbar an dröhnender Wiedergabe von Tönen dieser Frequenz, so müssen Sie nicht verzweifeln. Kennen Sie die exakte Resonanzfrequenz (durch Messung ermittelbar), so gibt es Abhilfe in Form von Bassabsorbern, auch Helmholtz*-Resonatoren genannt. Auf die Berechnung dieser trickreichen Bassfallen wollen wir im folgenden Abschnitt etwas näher eingehen.

 

3. Verminderung der Eigenmoden durch Helmholtz-Resonatoren

 

Querschnitt durch einen Helmholtzresonator

 

Helmholtz-Resonatoren arbeiten ähnlich wie Bassreflexboxen, nur mit umgekehrter Wirkung. Durch ein meist kanalförmig nach hinten erweitertes Loch wird ein kleines Resonatorvolumen an das Volumen des Hörraumes akustisch angekoppelt. Während das Bassreflexrohr einer Bassreflexlautsprecherkonstruktion nun die Schallwellen einer bestimmten Bassfrequenz, die vom Tieftöner nach hinten ins Lautsprechergehäuse abgestrahlt werden, nach außen in den Raum umlenkt und so die Basswiedergabe des Lautsprechers im Bassbereich verstärkt, bewirkt der Helmholtz-Resonator das umgekehrte. Er ist wie das Bassreflexrohr auf eine bestimmte Resonanzfrequenz abgestimmt. Diese Resonanzfrequenz stimmt sinnvollerweise mit der zu dämpfenden Raumeigenmode überein. Bei perfekter Abstimmung (dazu muss die Frequenz der zu dämpfenden Eigenmode möglichst exakt bekannt sein) entzieht der Resonator dem Raum im Bereich der Eigenmode Schallenergie, die in seinem Inneren durch Dampfungsmaterial unschädlich gemacht wird. Im Hörraum selbst verbleibt bei der Resonanzfrequenz deutlich weniger Schall, wodurch das Dröhnen im Bereich der Resonanzfrequenz effektiv reduziert wird.

Sie können Helmholtz-Resonatoren teuer kaufen, sie sind aber auch recht einfach selbst zu konstruieren. Zunächst müssen allerdings in jedem Fall die Raumresonanzen möglichst genau gemessen werden.

 

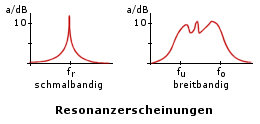
Resonanzerscheinungen

 

Relativ einfach sind scharfe Resonanzen bei einzelnen Frequenzen zu messen (im Bild links). Dabei spielt man einen gleitenden Sinuston in den Raum ein und misst den Schalldruck mit einem Schalldruckmessgerät. Man erhält eine Kurve, deren Maximum die Resonanzfrequenz fr angibt.

 Bei breitbandigen Überhöhungen führt die Frequenzanalyse mittels Rauschen zu exakteren Ergebnissen. Am sinnvollsten wird es sicher sein einen Fachmann den Raum durchmessen zu lassen, da dieser die Situation am besten beurteilen kann und auch über hochwertiges Messequipment verfügt.

Stehen die zu dämpfenden Resonanzen fest, so kann man relativ einfach mittels einiger mathematischer Formeln einen Helmholtzresonator konstruieren. Man benötigt für eine sinnvolle Berechnung drei verschiedene Formeln. Zunächst gilt für die Resonanzfrequenz des Resonators:

 

Formel fÃŒr die Resonanzfrequenz des Helmholtz-Resonators

 

Schauen wir uns diese zugegebenermaßen nicht ganz einfache Formel näher an. Zunächst finden sich zwei alte Bekannte wieder, die Schallgeschwindigkeit v und das Volumen V. Hier steht V allerdings im Gegensatz zu unseren bisherigen Formeln nicht für das Volumen des Hörraumes, sondern für das Volumen des Helmholtz-Resonators.

Wer sich in der Mathematik etwas auskennt, der kennt den griechischen Buchstaben π (kleines pi) zur genüge. Es handelt sich dabei um eine oft benötigte Konstante mit dem ungefähren Wert 3,14159. Überall wo π steht können Sie sich daher 3,14159 denken.

 L stellt die Länge des Reflexkanals des Resonators dar. R ist der sogenannte equivalente Radius einer Öffnung. Ist die Öffnung kreisförmig, so ist der equivalente Radius R identisch dem Radius der Öffnung r nach

 

 

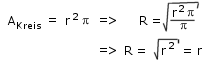
Ist die Öffnung dagegen anders geformt, so muss der equivalente Radius aus der Wurzel aus Flächeninhalt geteilt durch π berechnet werden.

 

Beispiel:
Wir möchten die Resonanzfrequenz eines Helmholtzresonators aus Holz feststellen. Der Resonator besteht aus einer quaderförmigen Kiste mit folgenden Innenmaßen:


Höhe: H = 0,7m
Breite: B = 0,3m
Länge: L = 0,5m


Das Wandmaterial sei MDF mit 19mm Wandstärke. In dieser Holzkiste befindet sich ein Loch mit den Abmessungen l = 0,1m und b = 0,2m. Die Schallgeschwindigkeit beträgt 340m/s.


Wir berechnen zunächst den equivalenten Radius des Loches:

 


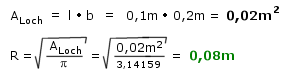
Als Länge L des Kanals verwenden wir in diesem Fall die Wanddicke des Materials, also 0,019m. Es fehlt nun noch die Berechnung des Innenvolumens der Kiste:

 


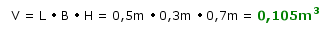
Jetzt setzten wir die Daten in die Formel für die Resonanzfrequenz ein:

 


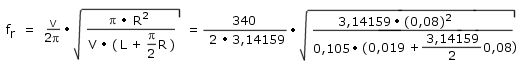
Daraus folgt nach einiger Rechnung die Resonanzfrequenz des Resonators:

 

 

Die Resonanzfrequenz ist jedoch nicht das einzige Kriterium, das bei der Konstruktion eines Helmholtz-Resonators berücksichtigt werden muss. Ein weiterer wichtiger Faktor ist die Güte des Resonators. Sie gibt an, wie breitbandig der Resonator arbeitet, ob er also eher zur Bekämpfung einzelner Resonanz-Peaks oder breitbandiger Überhöhungen geeignet ist. Auch die Güte Q lässt sich über eine mathematische Formel berechnen:

 

 

Auch in dieser Formel steht V für das Volumen des Resonators, L für die Kanallänge und A für den Flächeninhalt der Resonatoröffnung. Interessant ist vor allem, dass die Güte Q in direktem Zusammenhang mit der Resonanzfrequenz f und den beiden Eckfrequenzen der Überhöhung fu und fo steht. Betrachten Sie hierzu eventuell nochmals obiges Bild zu Resonanzerscheinungen, um sich die Lage von fu und fo klar zu machen. Beide Eckfrequenzen liegen dort, wo der Pegel der Überhöhung um 3dB gefallen ist. Lösen wir die Formel nach fu - fo:= Δ f auf, so erhalten wir eine Formel für die Bandbreite des Resonators:

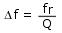
Beispiel:
Betrachten wir wieder unseren Resonator aus obigem Beispiel. Wir wollen jetzt seine Güte Q und seine Breitbandigkeit Δ f herausfinden. Dazu nochmals die Werte:


Volumen: V = 0,105m3
Kanallänge: L = 0,019m
Kanalquerschnittsfläche: A = 0,02m2
Resonanzfrequenz: fr = 62,26Hz


Wir berechnen zunächst die Güte:

 


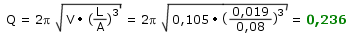
Aus der Güte Q = 1,885 können wir jetzt die Bandbreite des Resonators leicht berechnen:

 


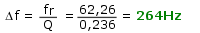
Der Resonator besitzt also eine Bandbreite von etwa 33Hz. Um die Eckfrequenzen fu und fo herauszufinden muss man wissen, dass sich die Resonanzfrequenz fr meist mittig zwischen den beiden Eckfrequenzen befindet. Setzen wir eine symmetrische Lage der Eckfrequenzen um die Resonanzfrequenz voraus, so folgt für die Eckfrequenzen:

 


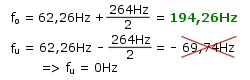
Der Resonator arbeitet also für alle Frequenzen im Bereich von 45 Hz und 83 Hz. Hätte die Berechnung eine negative Eckfrequenz zur Folge, so würde der Resonator alle Frequenzen von 0 Hz bis zur oberen Eckfrequenz schlucken (in der Realität existieren schließlich keine negativen Frequenzen). Für die Praxis eignet sich der von uns berechnete Resonator kaum. Der Dämpfungsbereich von 45 Hz und 83 Hz ist zu breit

Bisher haben wir unsere mathematischen Berechnungen nur auf den Resonator selbst beschränkt. Der umgebende Raum wurde bisher völlig außer acht gelassen. Leider besitzt aber gerade dieser Raum großen Einfluss auf die Wirksamkeit des Helmholtzresonators. Die Funktion ist nur dann gewährleistet, wenn das Resonatorinnenvolumen optimal auf das Raumvolumen abgestimmt ist. Nur wenn Raumvolumen und Innenvolumen im richtigen Verhältnis stehen, kann der Resonator funktionieren. Um diese Tatsache mathematisch vernünftig beschreiben zu können existiert der Koppelfaktor k für den folgende Berechnungsformel benötigt wird:

 

 

Achtung: Das Volumen V muss bei dieser Formel in Kubikcentimetern (cm3) eingesetzt werden! Will man also den Wert von oben verwenden (V = 0,105m3), so muss ein zusätzlicher Faktor 106 multipliziert werden. Der Kopplungsfaktor erhält damit die Einheit cm3pro s3. Die einzige neue Größe in dieser Formel ist der Anordnungsfaktor F. Durch ihn wird der Aufstellungsort des Resonators im Raum mit in den Kopplungsfaktor einbezogen. Gebräuchliche Werte für F zeigt die folgende Tabelle:

 

Standort Raumecke Raumkante eingelassen in Wand freie Aufstellung
Anordnungsfaktor F 8 4 2 1

 

Der Kopplungsfaktor hat großen Einfluss auf die Konstruktion des Helmholtzresonators. Durch ihn wird festgelegt, wie stark der Resonator bei seiner Resonanz dämpft. Ein großer Kopplungsfaktor bis zu 0,5 bewirkt dabei eine sehr starke Dämpfung der Resonanzstelle während kleines K um 0,02 die Resonanz nur sehr schwach dämpft. Durch geschickte Wahl des Aufstellungsortes, sowie Resonatorvolumen und Güte kann so jede Raumresonanz fast beliebiger Größe sehr effektiv vermindert werden.

In der Praxis wird es natürlich nicht wie in unseren Beispielen so sein, dass ein Resonator vorgegeben ist, von dem Werte berechnet werden müssen. Vielmehr wird das einzige, was durch die Messung vorgegeben ist die Resonanzfrequenz, die beiden Eckfrequenzen und das Ausmaß der Überhöhung sein. Wir wollen jetzt auch nur von diesen Werten ausgehen. Aus den gegebenen Frequenzen lässt sich leicht über

 

 

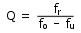
Q errechnen. Damit liegt die Güte unseres Helmholtzresonators bereits fest. Aus dem Ausmaß der Raumresonanz können wir einen Ungefährwert des Kopplungsfaktors bestimmen. Dieser Wert sollte zwischen 0,02 (kleine Überhöhung) und 0,5 (große Überhöhung) liegen.In der Formel für den Kopplungsfaktor sind nun noch zwei Unbekannte zu bestimmen, nämlich das Volumen V des Resonators sowie der Anordnungsfaktor F. Ist eine Aufstellung in der Raumecke möglich, so kann das Volumen gering gewählt werden. Kann der Helmholtz-Resonator allerdings nur in der Raummitte aufgestellt werden, so muss sein Volumen rund acht mal so groß ausfallen wie bei Eckaufstellung. Bei wandnaher Aufstellung halbiert sich sein Volumen gegenüber freier Aufstellung.

Damit liegt auch das Volumen des Resonators fest. Abschließend müssen wir die Größe der Öffnung in unserem Resonator herausfinden. Dazu setzen wir die bisherigen Ergebnisse in die Formel für Q ein (es kann auch die Formel für fr verwendet werden, dann wird die Rechnung aber komplizierter und aufwendiger). Die Formel wird nach L/A aufgelöst:

 

 

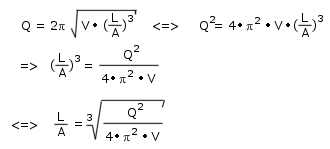
Nun ist die Berechnung der Öffnungsmaße nicht mehr schwer. Man legt entweder A oder L beliebig fest und berechnet anschließend den benötigten übrigbleibenden Wert aus der obigen Formel.

Helmholtz-Resonator der Firma VATTER

Der praktische Aufbau des Resonatorgehäuses erfolgt am leichtesten aus Holz. Achten Sie beim Design darauf, dass die Öffnungsfläche auch wirklich in eine der Seiten hineinpasst. Problematisch für das durchschnittliche Wohnzimmer ist bisweilen das doch recht große Volumen. Insbesondere Resonatoren für Frequenzen unterhalb von 40Hz werden recht großvolumig. Nicht jeder hat den Platz sich unter Umständen mehrere große Holzkisten in die Wohnung zu stellen - ganz abgesehen vom optisch nicht sehr ansprechenden Äußeren der Holzkisten. Bisweilen können Helmholtz-Resonatoren aber geschickt in die Wohnung integriert werden. Beispielsweise in eine Regalwand, oder als Unterbau für einen Tisch. Fertig zu kaufende Modelle können gerade unter optischen Gesichtspunkten oft als Vorbild verwendet werden.

Tipp:

Wer sich die Berechnung des Helmholtz-Resonators erleichtern will, der sollte sich dieses Online-Berechnungsprogramm näher ansehen!

 

4. Verbesserung der Nachhallzeit im Tieftonbereich: Plattenschwinger

Neben den Helmholtz-Resonatoren existiert noch eine weitere Möglichkeit die Wiedergabe im Hörraum im Bereich tiefer Frequenzen zu verbessern. Dazu werden sogenannte Plattenschwinger verwendet. Ein Plattenschwinger ist bereits dann gegeben, wenn eine Holzplatte mit einigem Abstand zur Raumwand befestigt wird. Das hinter der Platte befindliche Luftvolumen und die Platte selbst ergeben dann ein Feder-Masse-System, das rund um eine Resonanzfrequenz fr schwingt. Die Bandbreite dieser Absorber kann durch gezielte Materialauswahl beeinflusst werden. Wird dämpfendes Material hinter die Platte eingebracht, so verbessert sich deren Wirkung im oberen Bassbereich, wie folgende Skizze verdeutlicht.

 

 

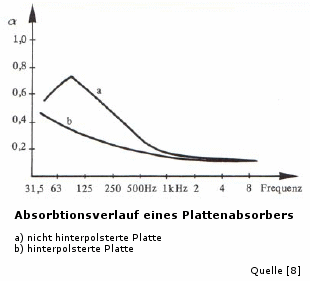
Im Gegensatz zum Helmholtz-Resonator werden Plattenschwinger weniger zur Reduzierung stehender Wellen verwendet. Der Vorteil der Plattenschwinger liegt vor allem in der Möglichkeit die Nachhallzeit eines Raumes für tiefe Frequenzen zu manipulieren. Im Tieftonbereich zu hallige Räume können mit Plattenschwingern relativ unkompliziert verbessert werden.

Als Materialien zum Bau solcher Absorber eignet sich in erster Linie wie oben bereits erwähnt Holz. Häufig werden Sperrholz oder Hartfaserplatten wie MDF eingesetzt. Bedenken Sie vor allem auch, dass bereits so banale Dinge wie die Rückwand eines Schrankes, der nahe an der Wand steht, als Plattenabsorber angesehen werden können.

Die Berechnung eines solchen Systems ist im Detail sehr aufwendig, was die Verwendung im Heimbereich stark einschränkt. Im professionellen Bereich, wo entsprechendes Messequipment und unter Umständen aufwendig konstruierte Modellräume zur Verfügung stehen, wird diese Art der Absorber jedoch mit großem Erfolg eingesetzt.

Auswirkungen der Absorber

In den folgenden beiden Diagrammen sind die Auswirkungen von Tieftonabsorbern auf den Frequenzgang eines kleinen Raumes im Bassbereich gezeigt:

 

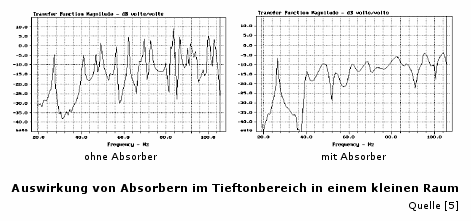
Frequenzgang eines kleinen Raumes mit Bassabsorbern und ohne

 

Im linken Diagramm ist ein Hörraum mit schallharten Wänden und ohne Bedämpfung dargestellt. Klar zu erkennen sind die heftigen Pegelschwankungen im gesamten dargestellten Bereich zwischen 20Hz und 200Hz. Diese Schwankungen sind ein klares Indiz für die starken Lautstärkeschwankungen im Bassbereich aufgrund stehender Wellen.

Im rechten Diagramm ist im Gegensatz dazu der Frequenzgang einesim Tieftonbereich gut gedämpften Raumes dargestellt. Beachten Sie vor allem den jetzt deutlich ausgewogeneren Frequenzgang zwischen 40Hz und 200Hz. Die Pegelschwankungen und damit die Lautstärkeunterschiede zwischen einzelnen Hörraumbereichen sind hier deutlich weniger ausgeprägt, was dem Klang zu gute kommt. Offensichtlich lohnt sich also eine Bedämpfung des Hörraumes im Bereich tiefer Frequenzen.

Herman von Helmholtz, 1821 - 1894

Quellenangaben:

  1. Handbuch der Elektroakustik; Günther Boye, Urbi F. Herrmann; Hüthig Buch Verlag Heidelberg; ISBN:3-7785-1575-6
  2. TMR Audio
  3. Dokument zur 5. Internationalen Internet- und Multimedia-Tagung (Zürich, 24.10.2002); "Raumakustik und Multimedia"; Autor: Kurt Eggenschwiler
  4. sengpielaudio.co.uk
  5. EMPA/HSR-Tagung 2001; "Holz in der Raumakustik"; Autor: Kurt Eggenschwiler
  6. Klang - Musik mit den Ohren der Physik; John R.Pierce; Spektrum der Wissenschaft; ISBN: 3-922508-72-3
  7. Audio Consequent
  8. Referat über Raumakustik

Computerprogramme zur Simulation der Raumakustik

  1. Programm von TMR-Audio
  2. CARA - Computer Aided Room Acoustics
  3. Programm zur Berechnung von Helmholtz-Resonatoren

 

Raumakustik 2 - Raumresonanzen, stehende Wellen

Im ersten Teil unserer Artikelreihe zur Raumakustik haben wir die Auswirkung von Schallreflexion im mittleren und hohen Frequenzbereich betrachtet. Wir sind dabei näher auf die durch Direkt- und Indirektschall hervorgerufenen Veränderungen des Klangbildes eingegangen. Im Tieftonbereich kommt ein anderer Effekt zum Tragen, den wir im folgenden etwas näher betrachten wollen. Es handelt sich dabei um die Entstehung von stehenden Wellen bei den Raumresonanzfrequenzen.

 

Inhaltsverzeichnis:

1. Prinzip der stehenden Welle
2. Überschlagsrechnung
3. Beispiel
4. Quellenangaben

 

1. Prinzip der stehenden Welle

Das Prinzip der stehenden Welle lässt sich besonders gut am Schwingen einer Gitarrensaite erkenntlich machen (siehe Bild oben). Wird die Saite um ihre Ruheposition ausgelenkt und anschließend losgelassen, so wandert die Auslenkung wellenförmig von der Startposition aus zu den beiden Enden der Saite.Allerdings kann sich diese Welle nicht über die feste Einspannung hinaus fortpflanzen. Daher wird sie am Ende der Saite reflektiert. Es kommt zu einer Überlagerung der hinlaufendenund rücklaufenden Welle. Die Wellen laufen nun so lange vom einen Saitenende zum anderen und wieder zurück, bis ihre Energie durch Reibung vollständig aufgebraucht ist. Durch Interferenzeffekte kommt es dabei in weiten Frequenzbereichen zu einer vollständigen Auslöschung der Wellen. Nurbei den sogenannten Resonanzfrequenzen bildet sich ein stationäres Schwingungsmuster aus. Dieses Muster wird als stehende Welle bezeichnet. Charakteristisch für stehende Wellen ist, dass bestimmte Orte innerhalb des Schwingungsmusters keinerlei Auslenkung um die Ruhelage erfahren. Diese Orte bezeichnet man auch als Schwingungsknoten. Alle andere Orte pendeln mehr oder weniger stark um ihre Ruheposition. Orte, an denen diese periodische Auslenkung den Maximalpegel erreicht, werden auch Schwingungsbäuche genannt. Dadurch, dass sowohl Knoten, als auch Bäuche ortsfest sind, sieht das sich ergebende Schwingungsmuster aus wie einefeststehende Welle, was die Namensgebung erklärt.
 

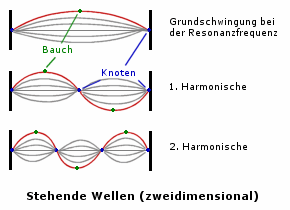
Stehende Wellen im Zweidimensionalen

Wichtig ist es zu wissen, dass die Gitarrensaite nicht nur mit einer einzelnen Frequenz schwingt. Charakteristisch ist zunächst die Grund- oder Eigenschwingung. Diese Schwingung macht die Tonhöhe des hörbaren Tones aus. Wie im Bild oben zu sehen ist die Grundschwingung dadurch gekennzeichnet, dass genau eine halbe Wellenlänge auf die Länge der Saite passt. Die Grundschwingungbesitzt also einen Bauch und keine Knoten, wenn man mal von den Knoten an der Einspannung der Saite absieht. Des weiteren schwingt die Saite mit Harmonischen erster bis h-ter Ordnung. Die Harmonischen sind für den satten angenehmen Klang der Gitarre verantwortlich.

Die erste Harmonische liegt bei der doppeltenFrequenz der Eigenschwingung. Demnach passt hier eine ganze Wellenlänge bzw. ein Knoten und zwei Bäuche auf die Saite. Die zweite Harmonische schwingt mit der dreifachen Frequenz derGrundschwingung. Es passen eineinhalb Wellenlängen der zweiten Harmonischen auf die Saite und damit zwei Knoten und drei Bäuche. Dieses Schema setzt sich weiter fort. Allgemein kann man schreiben:

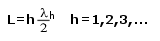
Diese Formel gibt eine Berechnungsmöglichkeit der Wellenlänge für höhere Harmonische bei gegebener Länge L der Saite.

Sicher kennen Sie den Unterschied wenn man an der Gitarre das "a" spielt und einen Sinusgenerator einen Sinuston mit einer Frequenz von 440Hz wiedergeben lässt. Beide Töne schwingen (grob) mit der gleichen Frequenz, dennoch klingt die Gitarre angenehm und harmonisch, während der Sinusgenerator eher einen unangenehm schrillen Pfeifton von sich gibt. Das liegt daran, dass der Sinusgenerator wirklich nur eine Schwingung von exakt 440Hz ausgibt. Die Gitarre spielt in Wirklichkeit nicht exakt bei 440Hz. Aufgrund der Oberschwingungen (=Harmonischen) kommen Frequenzkomponenten hinzu, die dem Sinussignal aus dem Generator fehlen. Der Generator klingt aus diesem Grund kühl, schrill und unangenehm.

Betrachten wir nun wieder unseren Hörraum. Auch hier bilden sich unweigerlich stehende Wellen, solange irgendwo im Raumparallel verlaufende Flächen vorhanden sind, was zumindest bei Decke und Boden fast immer der Fall sein dürfte. Je mehr parallele Flächen vorhanden sind, desto stärker wird die Bildung von Resonanzen begünstigt.Diese parallelen Flächen wirken auf die Schallwellen wie die Einspannungen der Gitarrenseite auf die Saitenschwingungen. Die Schallwellen werden von der Wand reflektiert und überlagern sich mit der hinlaufenden Welle. Genau wie die Welle auf der Gitarrensaite wandert nun die Schallwelle immer wieder zwischen den beiden parallelen Wänden hin und her, bis ihre Energie aufgebraucht ist. Es entsteht eine stehende Welle. Die Länge der Gitarrensaite wird dabei vom Abstand zwischen den Wänden übernommen. Dieser Abstand misst in der Regel einige Meter, weshalb sich in der Praxis nur stehende Wellen im Tieftonbereich bilden können. Man spricht auch von den Eigenmoden des Raumes.

 

2. Überschlagsrechnung

Der Abstand zwischen zwei parallelen Wänden beträgt 5m. Wie groß ist die Wellenlänge derGrundschwingung der sich bildenden stehenden Welle?

Wir lösen obige Formel nach λ auf und setzen h = 1 (Grundschwingung ist gefragt).
Ergebnis: λ = 10m
Hiervon lässt sich über f = v/λ mit v = 340m/s die Resonanzfrequenz der Wandanordnung berechnen:
f = 34Hz => tiefer Bassbereich</´p>

Die obige Überschlagsrechnung zeigt deutlich, dass die dominierenden Eigenschwingungen bzw. die Resonanzfrequenzen des Raumes im Bassbereich liegen. In der Praxis lassen sich die Frequenzen der stehenden Wellen leider bei weitem nicht so einfachwie in unserer Überschlagsrechnung berechnen. Der Grund dafür ist darin zu suchen, dass sich die stehenden Wellen anders als bei der Gitarrensaite nicht nur inzwei Dimensionen ausbilden, sondern in dreien. Auf diese Weise sind bei geometrisch kompliziert konstruierten Räumenextrem aufwendige mathematische Rechnungen nötig, um die Resonanzfrequenzen des Raumes zu bestimmen. Mittels Taschenrechner sind diese Rechnungen nicht vernünftig durchzuführen. Im folgenden soll daher nur gezeigt werden, wie für einen quaderförmigen Raum mit ideal reflektierenden Wänden (α = 0) überschlagsmäßig alle Resonanzfrequenzen bis zweiter Ordnung gefunden werden können. Wer sich die Arbeit deutlich erleichtern will, der sollte ein gutes Raumsimulationscomputerprogramm ins Auge fassen. Beispiele finden Sie am Textende.

Aufgrund der dreidimensionalen Anordnung der Wände eines Hörraumes haben wir es bei den folgenden Berechnungen mit einer recht komplexen Formel zu tun:

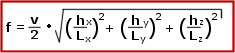
Berechnung der Resonanzfrequenzen eines Hörraumes

Diese Formel bedarf sicherlich noch einiger Erklärung. Zunächst stellt v die Schallgeschwindigkeit innerhalb des Raumes dar. Da ein üblicher Hörraum sicher immer mit Luft gefüllt ist, gilt bei 20 °C in etwa v = 340 m/s. Unter der Quadratwurzel stehen mehrere Buchstaben L mit Index x, y, z. Dabei ist Lx die Raumabmessung inx-Richtung eines willkürlich gewählten dreidimensionalen Koordinatensystems, Ly und Lz sind entsprechenddie Abmessungen in den anderen beiden Raumrichtungen.

Der Buchstabe h, der ebenfalls unter der Quadratwurzel steht, klassifiziert die Ordnung der Harmonischen. Auch hier gibt der Index die jeweilige Ortskoordinate an.

Insgesamt stellen sich die Resonanzen im dreidimensionalen Raum deutlich komplexer dar als im zweidimensionalen.Zunächst sind die Hauptmoden 1. Ordnung (Grundresonanzen) in allen drei Raumrichtungen zu berechnen. Diese Grundresonanzen breiten sich in exakt eine Raumrichtung aus, daher kann nur eine der h-Koordinaten von Null verschieden sein. Setzt man beispielsweise hx=1 und hy=hz=0, so erhält man die Grundresonanz in x-Richtung. Aus diesem Grund vereinfacht sich die komplexe Gleichung oben bei der Berechnung der Grundresonanzen deutlich. Im folgenden das Ergebnis, wobei wir v/2 gleich zu 170 berechnet haben:

 

Berechnung der Grundresonanzen

 

Für die Berechnung der Nebenmoden 1. Ordnung nehmen wir wieder unsere obige Gleichung her, allerdings mit dem Unterschied, dass jetzt mindestens zwei der h-Variablen gleich eins gesetzt werden müssen. Daraus resultieren vier Nebenmoden erster Ordnung. Leider kann unsere Anfangsgleichung jetzt nicht mehr ganz so weit vereinfacht werden. Trotzdem fällt zumindest in drei Fällen ein Term unter der Wurzel weg:

Berechnung der 1. Harmonischen

Als nächstes erfolgt die Berechnung der zweiten Harmonischen. Dazu beginnt man wieder wie bei der Berechnung der Grundresonanzen, nur dass jetzt alle Möglichkeiten ausgeschöpft werden, in denen zwei h-Werte gleich Null und ein h-Wert gleich 2 ist:

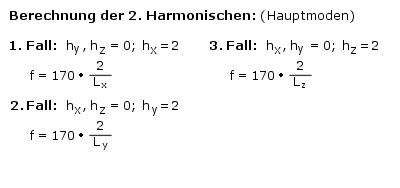
Berechnung der 2. Harmonischen

Das sind nur die Hauptmoden 2. Ordnung. Nun müssen alle Möglichkeiten, dass ein h gleich zwei, eines gleich eins undeines gleich Null ist, durchgespielt werden. Anschließend kommt man auf weitere Resonanzfrequenzen, wenn man zwei h´s gleich zwei setzt und eines gleich null. Es müssen also alle Kombinationen an Zahlen durchgespielt werden, wobei jedes der drei h´s 0, 1 oder 2 als Wert annehmen darf. Erst dann hat man alle Nebenmoden 2. Ordnung berechnet. Harmonische höherer Ordnung erhält man dann genauso, allerdings liegt der Wertebereich der h´s zum Beispiel bei der dritten Harmonischen zwischen 0 und 3, bei der vierten zwischen 0 und 4, u.s.w. Man sieht, dass sich der Rechenaufwand enorm steigert, daher nochmals der Hinweis auf die Computerprogramme im Anhang an diesen Artikel sowie ein äußerst praktisches Online-Tool, mit dem Sie die wichtigsten Resonanzen für den quaderförmigen Hörraum schnell berechnen können. Doch auch ohne den PC lassen sich schon aussagekräftige Berechnungen durchführen. Dadurch, dass die Schallintensität mit der Ordnung der Resonanz stark abnimmt, also Resonanzen höherer Ordnung deutlich leiser ausfallen, als die Grundresonanz, genügt es in der Praxis eine Berechnung bis zweiter Ordnung durchzuführen (das ist gerade noch mit dem Taschenrechner zu bewerkstelligen).

 

3. Beispiel

Wir wollen die ersten Resonanzfrequenzen eines quaderförmigen Hörraumes mit den Abmessungen

x = 3m,
y = 4m,
z = 2,5m

berechnen.

Zunächst berechnen wir die 3 Grundresonanzfrequenzen:

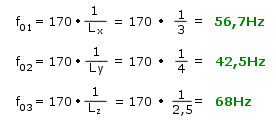
Berechnung der Grundresonanzen

Deutlich ist zu sehen, dass alle Resonanzen im Bassbereich liegen. Als nächstes müssen die Harmonischen erster Ordnung berechnet werden.
Der Übersichtlichkeit wegen ist nur ein Beispiel der ersten drei Fälle voll ausgeführt:

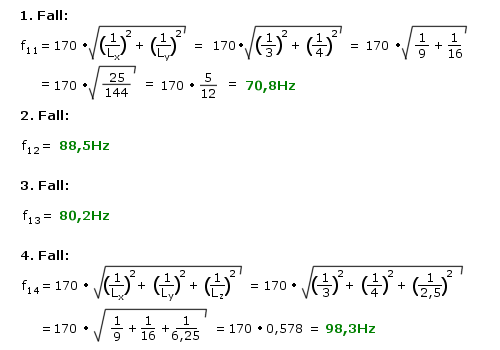
Berechnung der ersten Harmonischen

Als letztes berechnen wir noch die ersten drei Harmonischen zweiter Ordnung.
Auch hier soll der Übersichtlichkeit halber die Ausführung auf ein Beispiel beschränkt bleiben:

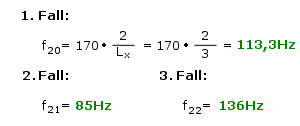
Berechnung der wichtigsten zweiten Harmonischen

Als Ergebnis lässt sich fest halten, dass der Beispielraum Resonanzen bei 42,5Hz, 56,7Hz, 68Hz, 70,8Hz, 80,2Hz, 85Hz, 88,5Hz, 98,3Hz, 113,3Hz und 136Hz aufweist. Beachten Sie, dass alle Frequenzen ausnahmslos im Bassbereich zu finden sind. Unberücksichtigt bleiben dabei Resonanzen höherer Ordnung als zwei. Klanglich werden sich sicher die Resonanzen erster Ordnung bei 42,5Hz, 56,7Hz und 68Hz am stärksten auswirken.

 


Anmerkung: Auch die Schallgeschwindigkeit ist kein absolut fester Wert. Bei 0°C beträgt sie beispielsweise nur noch 330m/s. Bei obiger Rechnung wurde eine Temperatur von 20°C angenommen. Die Temperatur Ihres Raumes sollte normalerweise im Bereich zwischen 15°C und 25°C liegen. In diesem Bereich ist es genügend genau mit 340m/s zu rechnen.

Verteilung von Knoten und BÀuchen im Hörraum

Doch was sagen nun diese Resonanzfrequenzen aus? Dazu betrachten wir obiges Bild. Es zeigt die Schalldruckminima (schwarz) und Schalldruckmaxima (weiß) bei Anregung eines Raumes mit den Abmessungen 3,4m x 5,4m mit einem Sinuston der Frequenz 163Hz. Die Schalldruckmaxima auf dem Bild kommen aufgrund von stehenden Wellen bedingten Effekten zustande, ebenso die Schalldruckminima. Klar dürfte sein, dass die Bäuche der stehenden Wellen die Maxima bilden, während Knoten zu Minima führen. Besonders extreme Knoten und Bäuche sind übrigens immer dann zu erwarten, wenn Harmonische verschiedener Ordnung die gleiche Resonanzfrequenz besitzen, wenn also beispielsweise die Resonanzfrequenz der Grundschwingung mit der der Harmonischen zweiter Ordnung übereinstimmt. In solchen Fällen sind bei dieser Frequenz starke klangliche Einbußen im Hörraum zu erwarten.

Versetzen Sie sich gedanklich in den Hörraum und variieren Sie Ihre Hörposition. Je nach deren Lage werden Sie vom 163Hz Ton viel hören, dann befinden Sie sich gerade in einem Wellenbauch, oder aber so gut wie gar nichts, wenn Sie Ihre Position in den Bereich eines Knotens gelegt haben. Wenn Sie nun zuhause in Ihrem Wohnzimmer eine ungünstige Hörposition einnehmen, wird Ihnen das gleiche geschehen. Sitzen Sie mittig im Raum, sitzen Sie fast garantiert in Bereich eines Knotens. Daher sollten Sie sich nicht wundern, wenn Sie von der Basswiedergabe Ihrer Lautsprecher nichts hören. Klingt Ihr Bass vielleicht dröhnend und aufdringlich? Dann haben Sie Ihren Hörplatz eher in einen Bauch verlegt. Wie Sie sehen haben stehende Wellen einen großen Einfluss auf die Basswiedergabe in Räumen. Wie man Fehler bei der Wahl der Sitzposition vermeidet, störende Resonanzen mindert oder gar stehende Wellen zu seinem eigenen Vorteil nutzt, das erfahren Sie im dritten Teil unseres Artikels zur Raumakustik.

 

4. Quellenangaben

  1. Handbuch der Elektroakustik; Günther Boye, Urbi F. Herrmann; Hüthig Buch Verlag Heidelberg; ISBN:3-7785-1575-6
  2. TMR Audio
  3. Dokument zur 5. Internationalen Internet- und Multimedia-Tagung (Zürich, 24.10.2002); "Raumakustik und Multimedia"; Autor: Kurt Eggenschwiler
  4. sengpielaudio.co.uk
  5. EMPA/HSR-Tagung 2001; "Holz in der Raumakustik"; Autor: Kurt Eggenschwiler
  6. Klang - Musik mit den Ohren der Physik; John R.Pierce; Spektrum der Wissenschaft
  7. Audio Consequent
  8. Referat über Raumakustik

Computerprogramme zur Simulation der Raumakustik

  1. Programm von TMR-Audio
  2. CARA - Computer Aided Room Acoustics