Über eine elektronische Methode, das Rauschen des 47kΩ Eingangswiderstands von MM Phono-Verstärkern mittels einer aktiven Eingangs-Resistanz zu verringern, um damit einen verbesserten Fremd- und Geräuschspannungsabstand zu erzielen. Ein weiterer Artikel des Autors und Fachmanns für Audiotechnik: Burkhard Vogel.
Im angelsächsischen Raum verbreitet, aber im deutschsprachigen Raum wenig bis überhaupt nicht behandelt, genießt die trickreiche Anwendung des "elektronischen Kühlens" von Widerständen an geeigneter Schaltungsstelle relativ wenig Beachtung. Sogenannte geeignete Schaltungsstellen in diesem Sinne liegen u. a. immer dann vor, wenn es sich um Parallelschaltungen eines Widerstandes festen Wertes mit einer Impedanz veränderlichen, weil frequenzabhängigen, Wertes handelt.
1. Phono-Verstärker Eingangsschaltungs-Situation
Typische Beispiele hierfür sind die Eingangsschaltungen von MM Phono-Verstärkern oder Tonkopf-Verstärkern von Tonbandgeräten. Wir konzentrieren uns in dieser Studie auf Phono-Verstärker. Alle gemachten Angaben lassen sich aber ohne weiteres auf Tonkopf-Verstärker entsprechend anwenden.
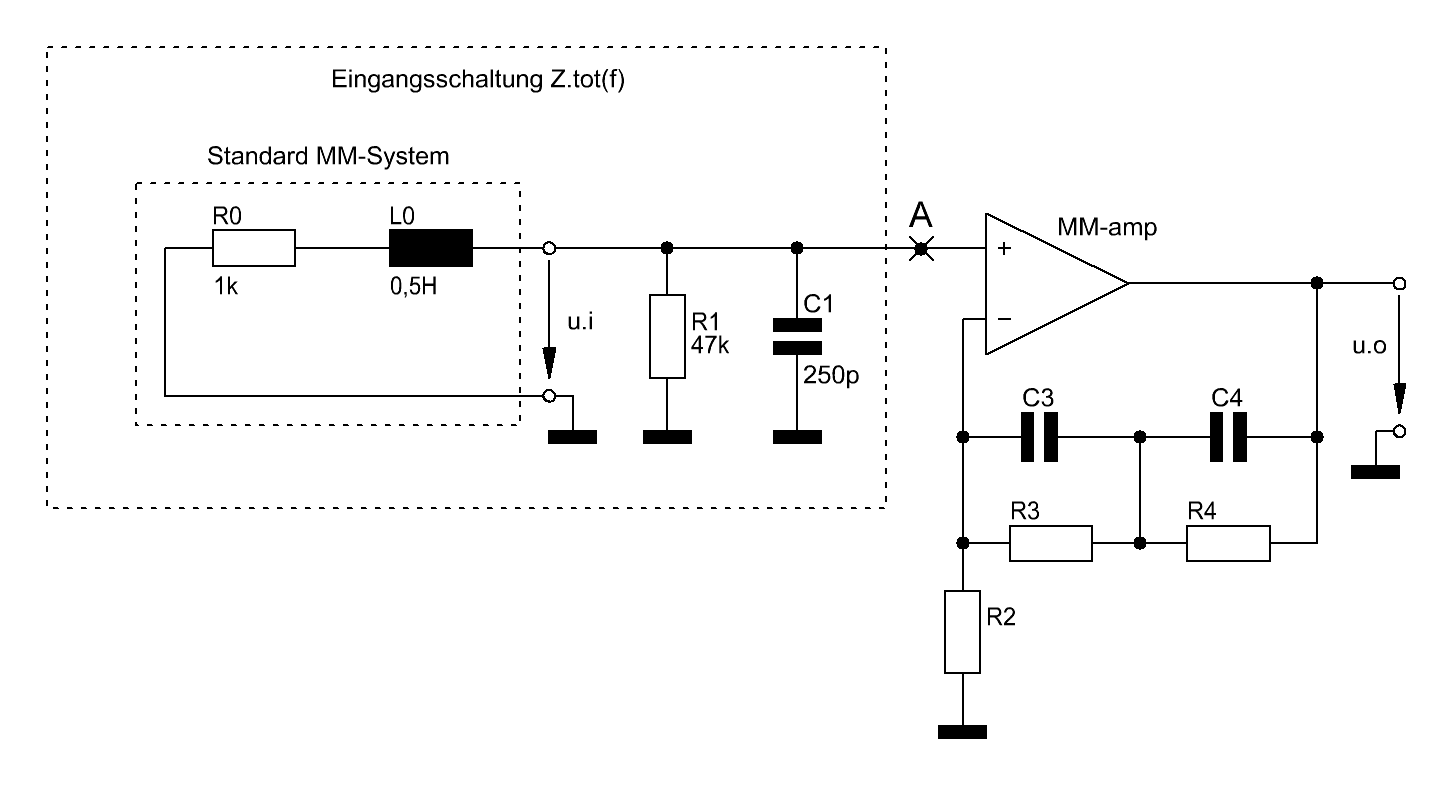
Die übliche Eingansschaltung eines MM Phono-Verstärkers ist in Abb. 1 gezeigt. Ihre Impedanz ist Ztot(f). Um Vergleiche mit den Testergebnissen von Testzeitschriften, wie etwa die von stereoplay, leichter zu ermöglichen verwende ich hier die gleichen Bauteilewerte für den sog. Standard MM Tonabnehmer. Dies ermöglicht die Berechnung des Fremdspan-nungsabstandes (SNriaa) oder des Geräuschspannungsabstandes (SNariaa) auf einer vergleichbaren Basis, denn das Ziel der Anstrengungen soll ja eine Verbesserung des SNs gegenüber dem Abb. 1-Fall nach Einführung der noch zu schildernden Maßnahmen sein.
Abb. 1 Situation der Eingangsschaltung eines typischen MM Phono-Verstärkers
Der Teil rechts von Punkt A ist ein typischer Vertreter von MM Phono-Verstärker, wie er heutzutage häufig mittels Op-Amps aufgebaut zu finden ist. Diese, aber auch solche, die diskret aufgebaut werden, sind inzwischen so rauscharm, daß sich eine weitere Jagd nach Verbesserungen kaum mehr zu lohnen scheint. Einzig solche mit Röhren in der Eingangsstufe zeigen SN-Werte, die häufig verbesserungswürdig sind, da sie schaltungsmäßig schlecht ausgelegt wurden und somit schlechtere SN-Werte zeigen als solche Phono-Verstärker, die mit Halbleitern bestückt sind. Wie man das macht habe ich ausführlich an anderer Stelle (s. den Literaturhinweis in Section 5) beschrieben.
2. Rauschproblem des Phono-Verstärker Eingangswiderstands R1
Das, was somit die Rauschprobleme eines Phono-Verstärkers eigentlich erzeugt, sitzt als R1 in dem Eingangschaltungskasten von Abb. 1, und um diesen Widerstand geht es im eigentlichen Verbesserungssinne. Wenn er weniger rauschen würde, wäre der SN der Gesamtschaltung automatisch besser.
Das Rauschen von Widerständen läßt sich mit der Formel (1) berechnen,
![]() (1)
(1)
wobei k die Bolzmann'sche Konstante mit 1,38065*10-23 VAsK-1, T die absolute Bauelemente-Umgebungstemperatur von z. B. 300K (Kelvin) und B1 der betrachtete Frequenzbereich von 1Hz ist. Das Ergebnis ist eine Rauschspannungsdichte, ausgedrückt in V/√Hz (Volt pro Wurzel aus Hertz). Für einen 47kΩ Widerstand ergibt dies 27.9nV/√Hz. Man kann die Rauschspannungsdichte eines Widerstands in nV/√Hz relativ einfach berechnen, indem man die Wurzel aus dem Widerstandswert, ausgedrückt in kΩ, mit 4,07 multipliziert. Es ergibt sich damit z. B. für einen 2,21kΩ Widerstand eine Rauschspannungsdichte von 4,07*√2,21 = 6,05nV/√Hz.
Verglichen mit dem Rauschen des 1kΩ Widerstand des MM Systems von 4.07nV/√Hz ist das Rauschen eines 47kΩ Widerstands sehr viel höher. Man könnte jetzt einwenden, daß bei einer Parallelschaltung zweier Widerstände nur das Rauschen des resultierenden Widerstandes R1||R0 zählt, was rein rechnerisch unter 4.07 nV/√Hz liegen müßte, da der resultierende Widerstand R1||R0 zählt, was rein rechnerisch unter 4.07 nV/√Hz liegen müßte, da der resultierende Widerstand <R0 ist. Dem ist leider nicht so. Jetzt kommt nämlich die rauschverstärkende Rolle der eigentlich rauschfreien Induktanz L0 ins Spiel. Diese Spule des MM Systems, deren Drahtwiderstand durch R0 gegeben ist, verändert ihren rauschfreien Blindwiderstand XL0(f) mit der Frequenz f, und zwar wie folgt:
![]() (2)
(2)
d. h., daß ihr Widerstand um so höher wird, je höher die Frequenz gewählt wird. Bei 20Hz sind das gerade einmal 62,832Ω, bei 20kHz aber 1.000 mal so viel, also 62,832kΩ.
Berücksichtigt man diesen Effekt bei der Rauschberechnung der Eingangschaltung und wir lassen hierbei aus Vereinfachungsgründen zunächst C1 als Abbild aller Kapazitäten zwischen MM System und MM Verstärkereingang außen vor, dann ergeben sich immer Werte der Rauschspannungsdichte, die größtenteils zwischen derjenigen von R0 und der von R1 liegen, in jedem Fall aber solche, die mit ihrem Durchschnittswert im Audio-Frequenzbereich von 20Hz bis 20kHz (= B20k) größer sind, als das auf den Eingang bezogene Rauschen des am Eingang kurzgeschlossenen MM Verstärkers rechts von A in Abb. 1.
Dieses liegt, unter Berücksichtigung aller seiner Rauschquellen, bei sehr guten Phono-Verstärkern im Bereich von <3nV/√Hz bei 1kHz. Röhren Phono-Verstärker mit z. B. einer selektiert rauscharmen ECC83 im Eingang liegen, bedingt durch das niederfrequente sog. Funkel-Rauschen (engl. 1/f-noise) mit seiner relativ hohen Eckfrequenz im B20k-Schnitt mit ca. 12nV/√Hz schon wesentlich höher. Ich habe bei meinen umfangreichen Untersuchungen sehr selten eine auf Rauscharmut selektierte ECC83 gefunden, deren Systeme Eckfre-quenzen des1/f-Rauschens unter 1kHz zeigen. Zumeist liegen sie zwischen 2kHz und 4kHz.
Man kann den resultierenden Widerstandsverlauf auch graphisch als durchgezogene Linie, wie in Abb. 2 gezeigt, darstellen. Man muß dabei in Betracht ziehen, daß das Rauschen im Frequenzbereich von 0Hz bis 10kHz gleichgewichtig dem Rauschen von 10kHz bis 20kHz zu werten ist. Beide Bereiche überstreichen gleich große Frequenzbereiche, die natürlich in der logarithmischen Darstellung von Abb. 2 ungleich groß herauskommen. Man sieht, daß sich der resultierende Betrag des Widerstandswertes Zi(f) im Bereich von 10kHz bis 20kHz immer über 20kΩ bewegt. Die gepunktete Linie (Betrag von Zi.tot(f)) zeigt die Verschlimmerung der Situation durch die immer vorhandene und rauschfreie Kapazitanz C1, hierbei mit 250pF angesetzt, die parallel zu R1 und R0+L0 liegt.
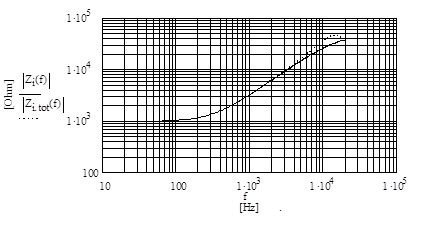
Abb. 2 Impedanz der Parallelschaltung von R0+L0 mit R1 sowie der zusätzliche C1-Effekt
Das frequenzabhängige Rauschverhalten der Parallelschaltung von R1 mit der Impedanz R0+L0 berechnet sich nun, hier beispielhaft ohne C1, so, daß die Rauschquellen von R1 (en.R1) und R0+L0 = Z0(f) (en.Z0(f)) über Spannungsteiler, die aus R1 mit Z0(f) gebildet werden (s. Abb. 3 und Appendix), zwei Rauschspannungen en.1(f) und en.2(f) ergeben, die entsprechend (3) zu summieren sind und somit die frequenzabhängige Gesamt-Rauschspannungsdichte en.i(f) der Eingangsschaltung ergeben.
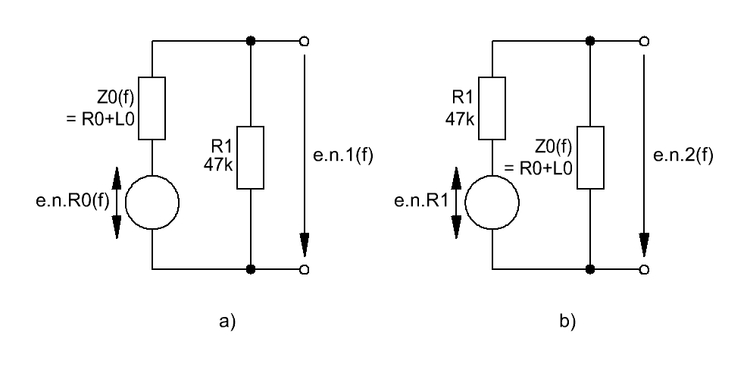
Abb. 3 Erzeugung der Rauschspannungen en.1(f) und en.2(f)
![]() (3)
(3)
Die entsprechende graphische Darstellung gibt Abb. 4 wieder. Die gepunktete Linie zeigt das Rauschen von R1 (= en.R1(f)), die gestrichelte Linie dasjenige von R0 (= en.R0(f)). Aus dem durchgezogenen Kurvenverlauf errechnet sich eine für B20k durchschnittliche Rauschspannungsdichte von 23,9nV/√Hz, welches in voller Größe in die Gesamt-Rauschspannung des Phono-Verstärkers eingehen würde, könnte man sie nicht verkleinern.
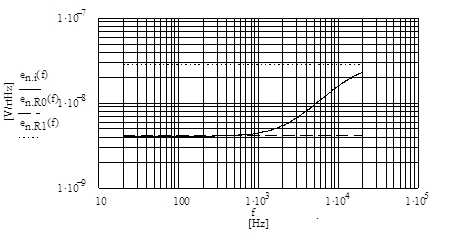
Abb. 4 Spannungsverlauf der Summe en.i(f) der Rauschspannungsdichten en.1(f) und en.2(f) in B20k:
durchgezogene Linie und ohne Berücksichtigung von C1
3. Lösungen zur Verringerung des R1-Rauschens
Eine Möglichkeit der Verkleinerung besteht z. B. darin, daß man R1 so weit herunterkühlt, daß seine Rauschspannung wesentlich kleiner würde, wie oben angegeben. In (1) bräuchte man nur den Wert für T = 300K auf z. B. Tcool = 14K setzen und schon bekäme man eine Rauschspannungsdichte von nur noch ca. 6nV/√Hz, was im Vergleich zur ursprünglichen R1-Rauschspannungsdichte von 27,9nV/√Hz eine Verringerung um den Faktor 4,65 bedeuten würde. Damit ergäbe sich eine erhebliche und positive Auswirkung auf den SN.
Nun kann man nicht einfach flüssiges Helium auf R1 packen, um solch niedrige Temperaturwerte zu erzielen. Das geht mit einem genialen elektronischen Trick etwas einfacher. Diesen Trick haben die belgischen Herren Hoeffelman und Meys 1978 im Journal of the Audio Engineering Society veröffentlicht (Improvement of the Noise Characteristics of Amplifiers for Magnetic Transducers, JAES Vol. 28, Nr. 12, S. 935ff). Verfeinert und mit praktischen Schaltungsvorschlägen versehen wurde die Sache späterhin durch den Niederländer Marcel van de Gevel 2003 in der Electronics World (Noise and moving-magnet cartridges, EW 10-2003, S. 38ff), bei dem ich auch zum ersten Mal auf den Begriff des "electronic cooling" gestoßen bin, sowie durch den Briten Douglas Self in seinem lesenswerten und neuesten Buch "Small Signal Audio Design" (Focal Press, 2010, ISBN 978-0-240-52177-0).
Das Kühlungsverfahren von R1 - und damit die Herabsetzung seiner Rauschspannungs-dichte - funktioniert wie folgt: R1 wird ersetzt durch die Schaltung nach Abb. 5. Diese erwirkt rein elektronisch den Kühlungseffekt, den man natürlich an und auf der Schaltung nicht spürt.
Die Funktion der Schaltung in Abb. 5 ergibt sich wie folgt: Punkt A entspricht dem Eingang des Phono-Verstärkers. Der OP-Amp OP1.1 bildet durch seine Schaltung mit Verstärkung 1 weder eine Belastung des Eingangs des Phono-Verstärkers noch eine Belastung des MM Systems. Er entkoppelt damit auch den nachfolgenden invertierenden Verstärker mit seiner Verstärkung Gcool von ca. -20 (das "-"-Zeichen zeigt nur die Invertierung des Eingangsignals um 180° an). OP2.1 verstärkt also das vom MM System gelieferte Eingangssignal um den Faktor Gcool und, das ist wesentlich, mit einer Phasenverschiebung von 180°.
Dieses invertierte, mit dem Eingangssignal aber 100% korrelierte, Signal trifft auf Rcool und dort auf das nichtinvertierte Eingangssignal, das in Rcool von A aus ebenfalls eingespeist wird. Der Misch-Effekt der beiden Signale ist nun der, daß es in Rcool, stellt man ihn sich in zwei Widerstände getrennt vor, einen Punkt B gibt, an dem eine Spannung von exakt 0V herrscht, es sich somit ein virtueller Massepunkt herausbildet, ähnlich demjenigen, der sich als virtueller Massepunkt bei OP2.1 am (-)-Eingang ergibt.
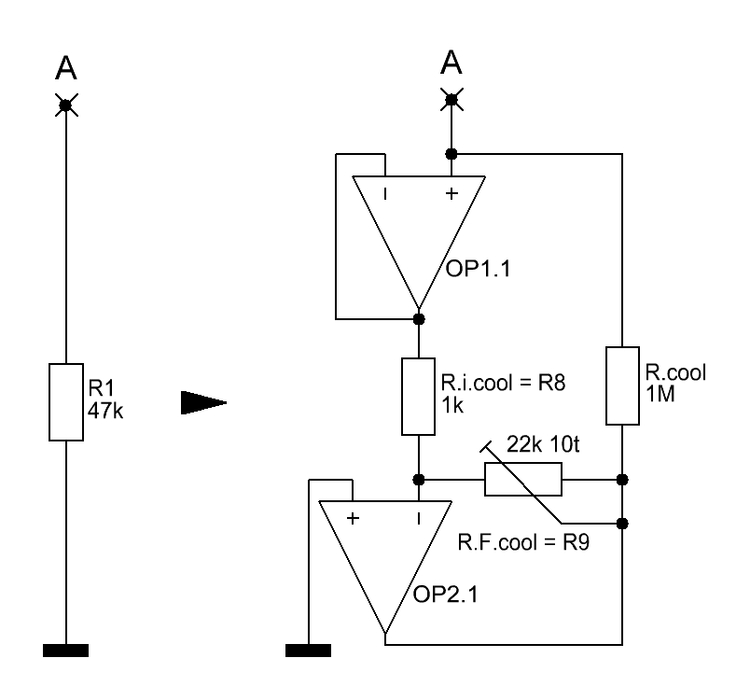
Abb. 5 Mögliche Schaltung zur elektronischen Kühlung von R1 nach Douglas Self
Trennt man z. B. Rcool bildlich gemäß Abb. 6 in einen oberen, A-nahen, Widerstand RA= 47kΩ und einen unteren (unter B liegenden) Widerstand RB auf, dann gibt die Formel (4) an, wie groß RB sein muß, damit sich zwischen den beiden Widerständen am Punkt B für alle an Punkt A eingespeisten Signale exakt 0,000V ergibt:
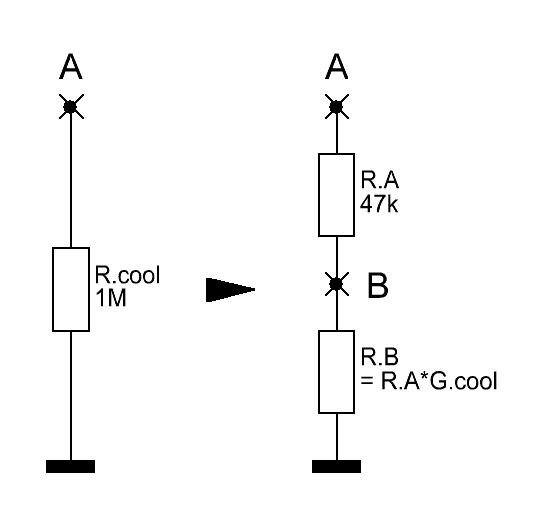
Abb. 6 Auftrennung von Rcool zur Identifizierung des virtuellen Massepunktes B
Dies gilt, wegen ihres korrelierten Verhaltens beim Durchgang durch OP1.1 und OP2.1 und Rcool, natürlich gleichermaßen für alle an Punkt A eingespeisten Rauschspannungen des MM Systems und die eingangsbezogene des MM Phono-Verstärkers. Zur Frage des eigenen Rauschbeitrags von OP1.1 und OP2.1 komme ich später noch.
Somit ergibt sich gemäß (5) für Rcool ein Wert, der sich in Abhängigkeit von Gcool errechnen läßt.
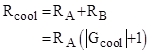 (5)
(5)
Um exakt auf den Wert von z. B. Rcool = 1MΩ zu kommen muß die Verstärkung Gcool von OP2.1 also mit RF.cool auf -20,277 eingestellt werden, oder - anders herum - wenn die Verstärkung von OP2.1 vorgegeben ist, z. B. mit -20, dann ergibt sich RB zu exakt 940kΩ und damit Rcool zu 987kΩ.
Bliebe man bei Rcool = 1MΩ und |Gcool| = 20, dann verschiebt sich gemäß Gleichungen (4) und (5) der 0V-Punkt B - und damit der Wert von RA auf 47,619kΩ, was außerhalb z. B. einer Toleranz von ± 1% läge, denn RA, zwischen A und dem virtuellen Masse-Punkt B gelegen, soll ja exakt R1 in Abb. 1 nachbilden.
Da RA auch den Wert von 47kΩ haben soll ergibt sich die Frage, was eigentlich diese zusätzliche Komplexität bringt? Dies erschließt sich erst so richtig bei der Betrachtung der von RA gelieferten Rauschspannungsdichte en.R.A. Diese entspricht, bedingt durch die gewählte Schaltung, eben nicht derjenigen des gleich großen Widerstands R1, sondern sie ist ca. 4,6 mal kleiner als die von R1. Sie ist mittels der Rauschspannungs-Gleichung (7) kalkulierbar. Dies ergibt sich aus der Betrachtung des durch (6) gezeigten und von Rcool erzeugten Rauschstromes in.R.cool, der damit, weil RA ein Teil von Rcool ist, in gleicher Höhe durch RA fließt:
Folglich gilt: 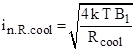 (6)
(6)![]() (7)
(7)
In Zahlen ausgedrückt ergibt sich mit den in Abb. 5 gezeigten Bauelementen das folgende Rauschstrom- und Rauschspannungs-Dichte-Bild:
• in.R.cool = 128,7 fA/√Hz
• en.R.A = 6,05 nV/√Hz anstatt 27,9nV/√Hz
Die elektronische Temperatur Tcool wäre damit - gerechnet mittels (1) - ca. 14,1K für einen 47kΩ Widerstand. Die Wirkung der aktiven Resistanz als Nachbildung und Ersatz von R1 kann man übrigens ganz einfach durch Simulation nachprüfen, indem man einen Spannungsteiler mit einem 47kΩ Hilfs-Widerstand und der Schaltung nach Abb. 5 aufbaut. Das sieht dann etwa so aus wie in Abb. 6 der rechte Teil, wobei RB durch die Schaltung nach Abb. 5 ersetzt wird. Man speist nun mittels eines Sinusgenerators ein beliebiges Sinus-Signal bei A ein und erhält bei B genau die Hälfte davon, wenn der Sinusgenerator einen Ausgangswiderstand von nahe 0Ω hat. Ansonsten muß sein Ausgangswiderstand beim Wert des Hilfs-Widerstands berücksichtigt werden.
4. Einfluß von OP1.x und OP2.y auf das Rauschen von RA
Ganz ohne Haken kommt man beim Ersatz von Elektronik durch bessere Elektronik selten aus. Auf die zweite zu schluckende Kröte, auf die Übersteuerungsfestigkeit der neuen Eingasschaltung, komme ich später zurück. Die erste Kröte besteht darin, daß OP1.1 und OP2.1 auch einen Rauschbeitrag liefern, der die noch zu zeigende theoretische SN-Verbesserung allerdings nur leicht verschlechtern wird.
Gegenüber der in Abb. 5 gezeigten Selfschen Lösung gibt es eine etwas rauschärmere, in Abb. 7 gezeigte, Variante, die allerdings rein rechnerisch nicht mehr als 0,1dB bringt, allerdings aber auch die Frage nach einer solchen Variante abschließend beantwortet.
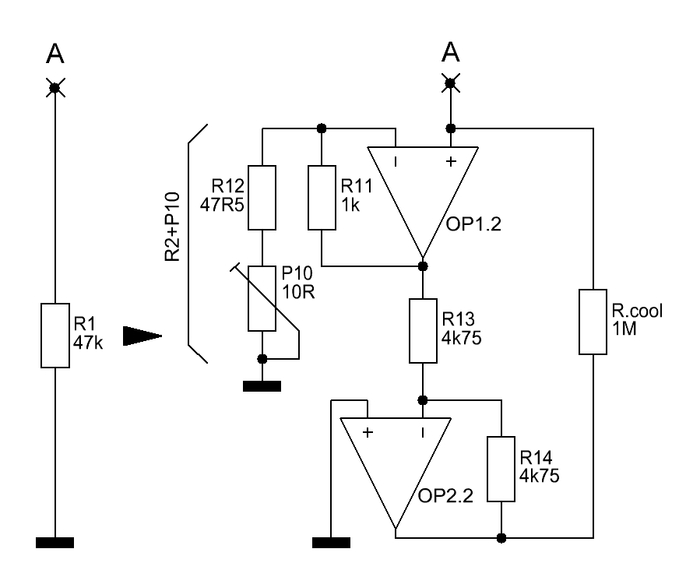
Abb. 7 Rauschärmere Variante zu Abb. 5
Der Unterschied zu Abb. 5 besteht darin, daß:
1. die in Abb. 7 von OP2.2 erzeugte Rauschspannung gegenüber der von OP1.2 erzeugten wg. der hohen Verstärkung (≥20) von OP1.2 gänzlich vernachlässigt werden kann, und
2. die Rauschspannung von OP1.2 in Abb. 7 wg. dem wesentlich kleineren Wert von R12+P10 (im Vergleich zu Ri.cool in Abb. 5) kleiner ausfällt als die Rauschspannung von OP2.1 in Abb. 5,
3. die Verstärkung von OP1.2+OP2.2 mit P10 auf -20,277 eingestellt wird.
Die in diesem Schaltungsteil durch OP1.2 (hier wirkt nur der eingangsbezogene Rauschstrom verschlechternd) und OP2.2 nebst ihren passiven Bauelementen erzeugte zusätzliche Rauschspannung en.cool ist 100% un-korreliert zu der am Punkt A anliegenden Summe der Rauschspannungen aus dem MM-System, aus RA, und aus dem Phono-Verstärker sowie aus der Eingangsrauschspannung von OP1.2. Diese Summe der zusätzlichen Rauschspannungen liegt am Ausgang von OP2.y in Abb. 5 als en.cool1 um |Gcool|+1 bzw. in Abb. 7 als en.cool2 um |Gcool| verstärkt an und wirkt damit über den Spannungsteiler von Rcool und der Impedanz der Eingangschaltung Ztot(f) (s. Appendix) verschlechternd auf die theoretisch erzielbare Rauschspannung am Punkt A in Abb. 1.
Die Rauschspannungsverstärkung (noise gain) ist im invertierenden Fall immer um 1 größer als die entsprechende Signalverstärkung. Diese Rauschspannungen sind damit automatisch SN verschlechternd. Folglich sind bei der Auswahl von OP1.x und OP2.y hinsichtlich ihres Rauschens bestimmte Regeln zu beachten, die weiter unten bei den Empfehlungen zur Sprache kommen werden.
5. Betrachtung der Rauschspannungsabstände
Basierend auf den Erkenntnissen aus meinem Buch 'The Sound of Silence' (Abk. TSOS, 2. Auflage 2011, Springer, Heidelberg, New York, ISBN 978-3-642-19773-4), in dem ausführlich mittels vieler Phono-Verstärker- und Meßschaltungen Rechen- und Meßmethoden und deren Vergleiche mit den entsprechenden SN-Meßergebnissen geschildert werden, erlaubt die in Abb. 8 gezeigte Testschaltung den mathematischen Ansatz ohne entsprechenden Testaufbau.
Die erwähnten Vergleiche münden sowohl im A-gewichteten als auch im nicht-gewichteten Fall bei solid-state basierenden, brummfreien, Phono-Verstärkern in einen Unterschied von höchstens ±0,5dB gegenüber den gemessenen Ergebnissen, sie liegen hingegen bei röhrenbasierenden, brummfreien, Phono-Verstärkern mit selektierten, rauscharmen Röhren bestenfalls bei ±1dB, solange die Eckfrequenz des niederfrequenten 1/f-Rauschens <1kHz ist. Einen Überblick über die wichtigsten Formeln gibt der Appendix.
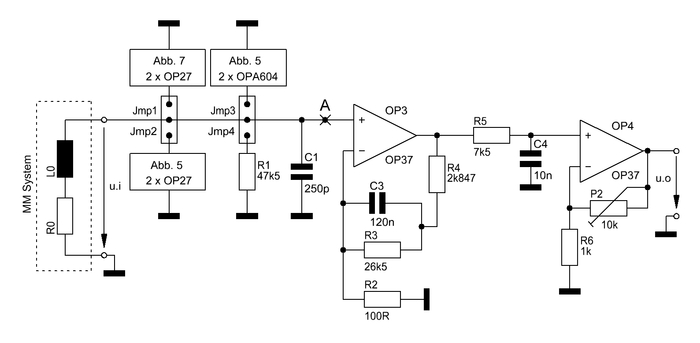
Abb. 8 Testschaltung zur SN-Berechnung von diversen R1 Resistanz-Formen
Die Berechnungen der auf 5mVeff nomineller Eingangsspannung bezogenen SNs basieren auf den in Abb. 9 gezeigten Spannungsverläufen am Punkt A der Schaltungen nach Abb. 1 bzw. Abb. 8, zur besseren Darstellung mit linearer Frequenzskala versehen.
Für den unbehandelten Phono-Verstärker gilt die durchgezogene Linie für en.tot(f), die beiden Varianten en.tot1(f) und en.tot2(f) mit aktiver Resistanz-Nachbildung nach Abb. 5 und 7 zeigen fast gleiche (gepunktete und gestrichelte) Linien.
Die positiven Auswirkungen bei Anwendung der Resistanz-Nachbildungen auf den SN sind nicht unbeträchtlich. Nimmt man eine Phono-Verstärker Eingangs-Rauschspannungs-dichte von ca. 3,3nV/√Hz bei kurzgeschlossenem Eingang an, dann ergibt sich ein eingangsbezogener Fremdspannungsabstand SNriaa (SNariaa für die Werte nach A-Filterung) für den Phono-Verstärker mit einem angeschlossenen Standard MM System und R1 von -76,0dB (78,8dB(A)). Der entsprechende Wert bei der "Kühlung" nach Abb. 5 errechnet sich zu SNriaa.1 -78,2dB (-81,5dB(A)) und nach Abb. 7 ergibt sich SNriaa.2 = -78,3dB (-81,6dB(A)). Mithin ergeben sich Unterschiede und Verbesserungen von 2,2dB, respektive von 2,3dB.
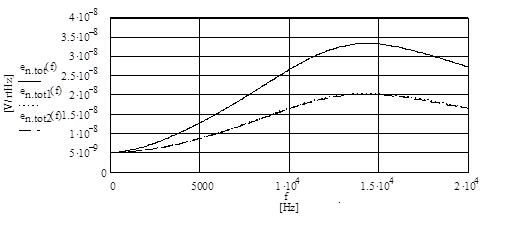
Abb. 9 Verläufe der Rauschspannungsdichten am Punkt A
Würde man einen noch rauschärmeren Phono-Verstärker benutzen, der z. B. nur mit einer Eingangs-Rauschspannungsdichte von 2,18nV/√Hz und einer Eingangs-Rauschstromdichte von 0,23pA/√Hz operiert, etwa mit 2x2SC2546 als Differenzverstärker mit je IC = 100µA geschaltet, so verbessern sich die SNs nochmals, und zwar von SNriaa = -76,9dB (-79,7dB(A)) auf SNriaa.1 = -79,9dB (-83,5dB(A)), respektive auf SNriaa.2 = -80,0dB (-83,6dB(A)), damit eine Verbesserung um -3,0dB, respektive um -3,1dB zeigend.
Dies bedeutet folglich, daß die Anwendung des beschrieben Verfahrens Sinn macht und sich eine erhebliche Verbesserung des SNs auch dann einstellt, wenn der eigentliche Phono-Verstärker selbst schon relativ stark rauscht. Eine Berechnung für eine röhrentypische Phono-Verstärker Eingangsrauschspannungsdichte von 12nV√Hz (ECC83) ergibt noch eine Verbesserung von 0,7dB gegenüber einem sowieso schlechten SNriaa von nur -71,7dB. Aber jedes dB zählt. Man kann dies leicht simulieren, indem man für OP3 in Abb. 8 einen LF356N wählt. Mit einer auf Rauscharmut selektierten E88CC lassen sich wesentlich niedrigere Phono-Verstärker Eingangs-Rauschspannungsdichten erzielen. Je nach gewählter Steilheit kommt man auf Werte von 5 bis 9nV/√Hz bei 1kHz.
Ohne Einbeziehung von C1 verbessern sich die rechnerischen Ergebnisse z. T. erheblich, bis zu 1,2dB ohne 250pF, aber um so mehr, je größer C1 sein müßte. Bedauerlicherweise geben Testzeitschriften praktisch nie an, welchen diesbezüglichen Wert sie bei ihren SN-Messungen ansetzen. Überdies geben sie häufig völlig sinnlose SN-Werte mit einer Eingangslast von 1kΩ an, die bar jeglichen Bezugs zur Realität sind. Der Durchschnittswert der Eingangslast liegt nämlich je nach MM-System um die 12kΩ.
Vergleiche mit Meßergebnisse machen überdies nur Sinn, wenn die Bandbreiten der jeweiligen Meßapparaturen bekannt sind. Die oben angegeben SN-Berechnungsergebnisse lassen sich am leichtesten mit Messungen vergleichen, die auf einer sog. äquivalenten Rausch-Bandbreite von B20k = 19.980Hz = 20kHz minus 20Hz beruhen, wie sie m. W. auch von stereoplay benutzt wird. Die Details hierzu finden sich entweder bei Tietze/Schenk, 12. oder 13. Auflage, Springer Verlag, oder in TSOS - nebst Filter-Schaltplan. Ansonsten muß umgerechnet werden, vorausgesetzt die äquivalente Meß-Rausch-Bandbreite ist bekannt.
Douglas Self hat in seinem o. a. Buch den Berechnungs- und Meßfall mit einem Shure M75ED 2 beschrieben. Mit einer Meßbandbreite von 21,6kHz kommt er dabei auf eine berechnete Verbesserung von -1,5dB und eine gemessene Verbesserung von -1,5dB wenn alle OP-Amps 5534A Typen sind und Rcool = 1MΩ, was die Funktionstüchtigkeit der Sache unterstreicht. Überdies ergab eine Diskussion mit ihm über die geschilderten Sachverhalte, daß die gezeigten Maßnahmen seinen Beobachtungen nach nicht zu einer Veränderung des Klirrfaktorbildes des Phono-Verstärkers führen. Ob die Meßbandbreite einer äquivalenten Rausch-Bandbreite entspricht ist aus dem Buch nicht erkennbar, allerdings bei Einsatz eines Audio Precision Meßinstruments wg. des steilflankigen Anti-Alias-Filters anzunehmen.
Ohne Unterstützung durch gemessene Werte lassen sich weitere Anwendungsmöglich-keiten aber mathematisch durchleuchten. Die beiden nächsten Sektionen sollen deshalb die Anwendung bei Step-up-Transformatoren für MC System Zwecke sowie des symmetrischen Eingangsschaltungsfalls anreißen. Eine Überprüfung der Mathematik am "lebenden" Objekt steht also noch aus. Allerdings läßt die Mathematik eine Abschätzung der Sinnhaftigkeit eines Versuchsaufbaus zu.
6. MC Systeme mit Trafo-Kopplung
Die Rauschminderungs-Funktion der beschriebenen aktiven Reaktanz-Schaltungen funktioniert um so besser, je höher der Wert der Eingangslast-Impedanz aus Widerstand und in Reihe geschalteter Induktanz ist; allerdings auf damit schlechterem SN-Ausgangsniveau aufbauend. Somit würde im entgegengesetzten Fall der SN-Verbesserungs-Effekt bei einem linearen MC Vor-Vorverstärker mit relativ niedrigem Ausgangswiderstand von ≤100Ω praktisch Null sein.
Dies trifft für einen MC Eingangstrafo nicht ganz zu, denn dieser erzeugt durch seinen Innenwiderstand zusammen mit dem am Eingang befindlichen MC System, entgegen der Mär vom rauschfreien Trafo, eine relativ hohe, auf seinem Innenwiderstand Rtr beruhende, zusätzliche Rauschspannung zu der des MC Systems, deren Summe durch den Einsatz der Schaltungen nach Abb. 5 oder Abb. 7 ebenfalls reduziert werden kann, allerdings nur in homöopathischen Dosen (s. Abb. 10).
Unter Anwendung der in Abb. 3 und (3) gezeigten Rechenvorschrift - und nur diese macht hier trotz augenscheinlicher Parallelschaltung von RA mit der durch die Trafoschaltung erzeugten resistiven Eingangslast Sinn - ergeben sich die in Abb. 10 in Abhängigkeit der MC-Impedanz RMC gezeigten SN-Verbesserungswerte SNimpr(RMC). Ich habe mich dabei als 1:10 Trafo eines sehr rauscharmen Jensen Transformers JT-44K-DX bedient (Rtr = 1.250Ω). Lundahl ist inzwischen mit seinem Typ LL9226 hinsichtlich der Rauscharmut von 1:10 MC Trafos mit etwas niedrigeren Ausgangsspulen-Widerständen auf einen Gesamt-Innenwider-stand von Rtr = 760Ω vorbeigezogen, was zu geringfügig besseren Rauschabstandswerten führt.
Die SNimpr Werte beziehen sich immer auf die Situation gegenüber einem 47kΩ Widerstand als R1 und einer angenommenen Phono-Verstärker Eingangs-Rausch-spannungsdichte von 3,3nV/√Hz. Auch hier gilt hinsichtlich der Rausch-Qualität des Phono-Verstärkers das Gleiche wie schon in Sektion 5 erwähnt. Generell beziehen sich die eingangsbezogenen SNs von MC Phono-Verstärkern auf eine nominelle Eingangsspannung von 0,5mVeff/1kHz.
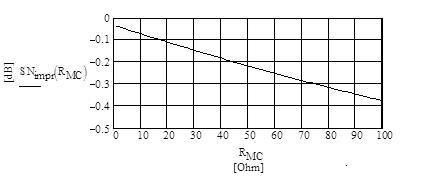
Abb. 10 SN-Verbesserung eines MC Phono-Verstärkers in Abhängigkeit der MC System Resistanz mit einem 1:10 Eingangs-Trafo an RA = 47kΩ im Vergleich zu einem Phono-Verstärker mit einem Eingangs-Widerstand R1 = 47kΩ
Spinnt man den Faden weiter zu höheren Transformator-Übersetzungsverhältnissen so kommt man zu der Erkenntnis: Je höher das Übersetzungsverhältnis des Transformators um so mehr verringert sich der nutzbare Eingangswiderstand des Phono-Verstärkers insgesamt und um so weniger Gewinn kann man aus der beschriebenen elektronischen Kühlung ziehen. Kurzum, es macht wenig Sinn, elektronisches Kühlen bei Phono-Verstärkern mit Trafo-Eingang zum Einsatz zu bringen, da die möglichen Gewinne im wahrsten Sinne des Wortes "im Rauschen untergehen".
7. Symmetrische Eingangslösung
Die ganze Sache funktioniert natürlich auch für den Fall eines symmetrischen Eingangs, den ich aber in Abb. 11 nur schaltungstechnisch und prinzipiell aufzeige. Die Rechenmethoden sind die gleichen und Phono-Verstärker mit symmetrischen Eingängen (und Ausgängen) hat Elektor m. W. in der Vergangenheit schon gezeigt.
Wer seinen Plattenspieler möglichst brummfrei, aber nicht in jedem Fall rauschärmer, und über eine längere Strecke an seinen Phono-Verstärker ankoppeln will greift zu dieser Lösung, die im MM System Fall aber nur richtig funktioniert, wenn das MM System nicht mit einem Ausgangspol pro Kanal an Masse liegt.
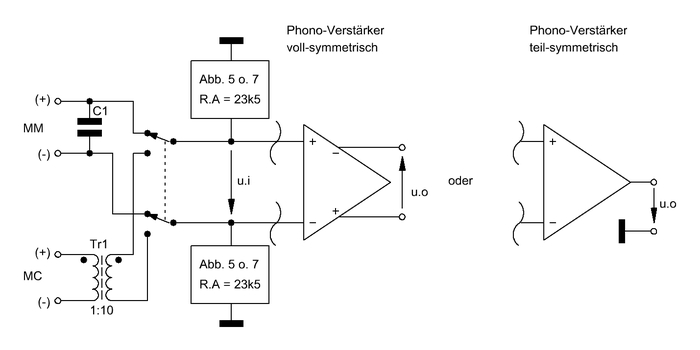
Abb. 11 Symmetrische Eingangslösung
Bei ui = 5mVeff erlaubt diese Lösung wg. der hälftigen Aufteilung auf die beiden Differenz-Eingänge jeweils eine höhere Verstärkungen Gcool zur Erzeugung der beiden Eingangs-Resistanzen (≈ -42), was aber noch nicht automatisch zu noch niedrigeren Rauschspannungen führt. Die somit erzeugten gleichgroßen und un-korrelierten Rauschspannungen werden nach den Regeln der Rauschspannungsaddition (s. (3)) addiert und ergeben dann erst einen Wert der kleiner ausfällt als im un-symmetrischen Fall, und zwar um 1/√2. Folglich liegt hierbei nicht nur eine SN-Verbesserung gemäß der weiter oben geschilderten Sektionen 2. - 5. vor, sondern zusätzlich eine Verbesserung der SNs gegenüber dem un-symmetrischen Fall. Dieser Fall ist also weiter verfolgenswert.
8. Empfehlungen
Die sog. Kühlung von Widerständen ist kein standardisierter Begriff und ergibt sich m. W. aus der Wort-Findung des weiter oben erwähnten Herrn van de Gevel. Die ursprüngliche Idee der Herren Hoeffelman und Meys basierte anstatt auf dem o. a. Rcool = 1MΩ auf einem Widerstand von 4,7MΩ, was eine weitere SN-Verbesserung ergäbe, wie man nun leicht nachrechnen kann, denn gemäß (6) verkleinert sich der von Rcool erzeugte Rauschstrom mit wachsendem Rcool.
Der entstehende Nachteil erschließt sich aber schnell durch (4) und (5). Damit würde Gcool sehr groß und der Ausgang von OP2 würde übersteuert werden. Mit |Gcool| ≈ 20,3 fährt man gemäß Empfehlung von D. Self bei Benützung von Op-Amps mit ± 15V Versorgungs-spannung am ungefährlichsten, denn die Übersteuerungsfestigkeit von OP2.y entspricht derjenigen des Phono-Verstärkers, dessen Ausgang bei 20kHz auf 1Veff bei 5mVeff Eingangsspannung eingestellt ist.
Aber dies kann nun jeder, in Abhängigkeit der nominalen Ausgangsspannung des MM-Systems sowie der gegebenen Schaltungsmöglichkeiten hinsichtlich Übersteuerungs-grenzen, selbst ausprobieren. Je höher die nominale MM System-Ausgangsspannung ist, um so weniger weit muß der nachfolgende Lautstärkeregler aufgedreht werden, um so besser fällt automatisch in gleichem Maße der SN aus, um so geringer ist dann auch der Bedarf einer SN-Verbesserung mittels elektronischer Kühlung. Ein MM System mit einer nominalen Ausgangsspannung von 10mV/1kHz/s/vertikal moduliert hat automatisch einen um 6dB besseren SN als eines mit nur 5mV/1kHz/s/vertikal moduliert.
Aufgrund der entsprechenden Berechnungen kristallisierten sich für die Auswahl von OP1 und OP2 die folgenden Regeln heraus:
Abb. 5 OP1.1:
• eingangsbezogene Rauschspannung spielt keine Rolle
• eingangsbezogener Rauschstrom spielt keine Rolle
Abb. 5 OP2.1:
• eingangsbezogene Rauschspannung spielt eine Rolle und geht in en.cool1 ein
• eingangsbezogener Rauschstrom spielt eine Rolle und erzeugt mit
Ri.cool und RF.cool eine in en.cool1 eingehende Rauschspannung
Abb. 7 OP1.2:
• eingangsbezogene Rauschspannung spielt keine Rolle
• eingangsbezogener Rauschstrom spielt eine Rolle und erzeugt mit R4+P10 und R5 eine zusätzliche Rauschspannung in en.cool2
• R4+P10 und R5 erzeugen eigene, eine Rolle spielende Rauschspannungen in en.cool2
Abb. 7 OP2.2:
Solange |Gcool|≥20 ist
• spielt die eingangsbezogene Rauschspannung keine Rolle
• spielt der eingangsbezogener Rauschstrom keine Rolle
• spielen die von Ri.cool (R13) und RF.cool (R14) erzeugten zusätzlichen Rauschspannungen keine Rolle
In der gezeigten Testschaltung lassen sich durch virtuelles Umstecken eines einzigen Jumpers auf die Steckplätze Jmp1 bis Jmp4 alle denkbaren Varianten durchrechnen. Will man die Testschaltung aufbauen so empfiehlt sich der Einsatz eines zusätzlichen DC-Servos, der vom Ausgang des Phono-Verstärkers auf den (-)-Eingang von OP3 wirkt, oder, und einfacher, eines C2 = 1mF, der vom Fußpunkt von R2 auf Masse geschaltet wird.
Appendix
1. Impedanz Ztot(f) der Eingangsschaltung:
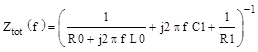 (8)
(8)
2. Rauschspannungsdichte en.tot(f) am Eingang des Phono-Verstärkers am Punkt A (en.riaa und in.riaa sind die äquivalenten Eingangsrauschspannungs- und Eingangsrauschstrom-dichte des MM phono-Verstärkers:
![]() (9)
(9)
3. Rauschspannungsdichte en.tot.1(f) (bzw. en.tot.2(f)) am Eingang des Phono-Verstärkers am Punkt A unter Berücksichtigung des zusätzlichen Rauschens der aktiven Resistanz en.cool1.eff(f) und/oder en.cool2.eff(f):
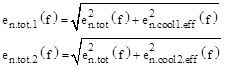 (10)
(10)
4. Erzeugung der Rauschspannungsdichten en.1(f) und en.2(f) unter Berücksichtigung von C1:
![]() (11)
(11)
Achtung: Bei Anwendung der aktiven Resistanz muß in der rechten Gleichung R1 durch RA und en.R1 durch en.R.A ersetzt werden
 (12)
(12)
5. en.riaa und en.cool lassen sich mit den in TSOS angegebenen, den Rahmen dieser Studie aber sprengenden, mathematischen Verfahren berechnen. Für en.riaa lassen sich für sehr rauscharme MM Phono-Verstärker ca. 2 bis 2,5nV/√Hz ansetzen, für bipolare und Op-Amp-basierende MM P-V ca. 3 bis 4nV/√Hz, für röhren-basierende MM P-V ca. 5 bis 12 nV/√Hz. Für en.cool1 bzw. en.cool2 kann man ca. 100nV/√Hz ansetzen, was sich aber über den Spannungsteiler aus Rcool und Ztot(f) auf ein Niveau von etwa 0,2 bis 0,3nV/√Hz bei 1kHz absenkt. Da der Effekt zw. en.cool1 und en.cool2 bei der SN-Ermittlung sehr klein wird (≤0,1dB) kann man im Prinzip auch darauf verzichten und man wählt Abb. 5 oder Abb. 7 je nach Gusto.
6. SN-Berechnung in [dB] mit Bezug auf 5mVeff/1kHz:
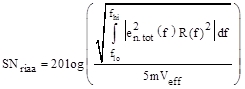 (13)
(13)
In unserem Fall hier ist flo = 20Hz und fhi = 20kHz. Die Berechnung von SNariaa [dB(A)] erfordert die multiplikative Einfügung des Quadrates der A-Filter-Übertragungsfunktion A(f) nach R(f)2 in (13). Diese Formel zeigt, durch das Integral bedingt, den SN in einer äquivalenten Rauschbandbreite von fhi - flo.
7. RIAA Übertragungsfunktion R(f), auf 0dB Verstärkung bei 1kHz normiert:
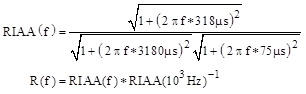 (14)
(14)
8. A-Filter Übertragungsfunktion A(f), auf 0dB Verstärkung bei 1kHz normiert:
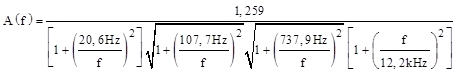 (15)
(15)
Autor: Burkhard Vogel
Umfangreiche Informationen zum großen Thema Audiotechnik finden Sie auch in den Fachbüchern von Herrn Burkhard Vogel: "The Sound of Silence" und "How to Gain Gain"
Diese Fachbücher sind im Springer-Verlag erhältlich:
|
|
"The Sound of Silence" von Burkhard Vogel Lowest-Noise RIAA Phono-Amps: Designer's Guide 2nd Edition., 2011, XXIII, 752 pages, 509 illus., 104 in color Hardcover, ISBN 978-3-642-19773-4 E-Book, ISBN 978-3-642-19774-1 http://www.springer.com/engineering/signals/book/978-3-642-19773-4
"How to Gain Gain" von Burkhard Vogel A Reference Book on Triodes in Audio Pre-Amps 2nd edition, 2013, XIV, 862 pages, 536 illus. Hardcover, ISBN 978-3-642-33032-2 E-Book, ISBN 978-3-642-33033-9 http://www.springer.com/engineering/electronics/book/978-3-642-33032-2
|