Delta-E (ΔE) is a measurement used to indicate how much a color deviates from an accepted standard. The higher the ΔE, the more inaccurate the color. Perfect color has a ΔE of zero. However, we need not achieve a ΔE of zero. This is because the human eye is only capable of detecting color difference at certain thresholds. The minimal detectable difference is anywhere from 1-2.5 ΔE. Unless a display has a fully-realized color management system (the vast majority do not), it is unlikely that calibration can achieve this level of performance for the primary and secondary colors. On the other hand, since virtually all displays have a full compliment of gray scale adjustments, calibration can often meet this standard for white.
History
ΔE came into widespread use after the CIE (Commission Internationale De L'Eclairage or International Commission on Illumination) announced in 1976 two new color appearance models that were to replace the standard XYZ model for measuring color that had been in place since 1931. Why the need for a new standard? The reason had to do with the fact that researchers had known for some time that the existing standard was not perceptually uniform. Perceptual uniformity is the ability of a color appearance model to plot changes in color that accurately represent what we actually see. The standard CIE diagram adopted in 1931 is NOT perceptually uniform. To see how, consider the diagram below, which is another representation of that 1931 CIE diagram.
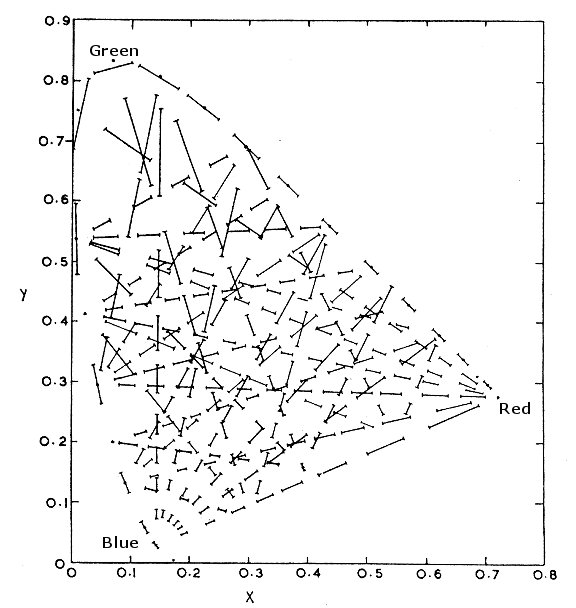
1931 CIE Chromaticity Diagram shown with perceptual non-uniformity indicators
Notice that the lines inside the diagram are not of equal length. This indicates that at different points on the graph, the distance between two colors plotted on the graph is much larger than the difference people see between those colors. What the CIE wanted was an approach that reduced this problem as much as possible. So, in 1976 the CIE recommended two new color appearance models that were significantly more perceptually uniform than the 1931 CIEXYZ standard represented by the chart you see above. These 2 standards were CIELUV and CIELAB, and they both improved perceptual uniformity from the 20:1 that the old system provided to about 4:1. Not perfect to be sure, but much better.
Why, you might ask did the CIE recommend TWO color appearance models to replace the single 1931 standard? Although both CIELUV and CIELAB were roughly equivalent in accuracy and CIELAB was clearly the favored model, CIELAB lacked something that many industries thought was essential: a chromaticity diagram that could use to plot the primary and secondary colors on straight lines. CIELAB did not offer this, but CIELUV did. Thus, the CIE offered both standards as something of a compromise. These two color appearance models also included a formula for calculating color differences from either Luv or Lab data. Thus, the 1976 decision left us with two color spaces and two color difference formulas CIELUV and CIELAB.
Unfortunately, color researchers began to notice that the 1976 color difference formulas both had their own problems with perceptual uniformity, so work continued. In 1994, CIE approved a new formula, based exclusively on the Lab data. This is known as CIE94.
CIE has continued to further refine methods for measuring color differences, including the adoption in 2000 of yet another Lab-based standard (CIEDE2000), which is VERY complicated and was never widely adopted outside of the textile industry. CIE94 continues as the most popular of the modern color difference formulas.
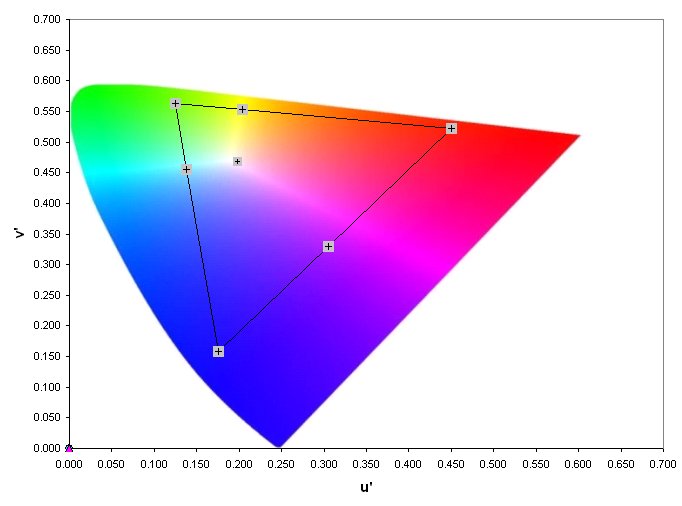
1976 u'v' Chromaticity diagram
Because the Luv color space and its associated 1976 formula is still the only approach that offers a linear chromaticity diagram (shown below), the CIELUV ΔE formula is still the most commonly used in the video industry. Despite this, most users continue to rely on the the old-fashioned 1931 chromaticity diagram, mostly we are more familiar with it. It is the default graph in ChromaPure.
Error Tolerance
Since ΔE offers a single number for measuring color error, we need to know the acceptable tolerances for video calibration. So too, one must be careful to specify which ΔE formula is being used since they scale color differences, well, differently. The biggest example of this discrepancy is that CIE94 scales much smaller than either of the 1976 formulas when reporting error in primary/secondary colors. When reporting errors in grayscale, it is identical to CIELAB.
I find SMPTE's standard for color error tolerance for Digital Cinema particularly useful. It is 4.0 CIELAB. That is equivalent to about 1.5 CIE94 for color.
Is ΔE all we have?
There are some problems with ΔE. Perhaps the biggest problem is the sheer proliferation of different standards. As mentioned above, a ΔE using one formula may mean something totally different than the same ΔE in a different formula. Another problem with ΔE tolerances is that a single number may represent a larger or smaller perceptual error depending upon the color being viewed and whether the error in question is one of saturation, hue, or lightness. Our eyes are not equally sensitive to these errors and the different formulas accommodate them differently.
In response to this problem, in addition to ΔE ChromaPure also uses a another metric for reporting color error, which is precise, uniform, and easy to understand. It is % error in lightness, saturation, and hue. Simply reporting that a shade of red has a CIE94 value of 2.4 is not nearly as useful as knowing that it has errors in L (-4.4%), S (1.4%), and H (0.0%). This tells us that the shade of red is too dim, slightly oversaturated, and with a correct hue.
