Die Entmystifizierung des Kabels

Der technisch interessierte und einigermaßen abgeklärte Leser mag sich kopfschüttelnd die Frage stellen, wie denn im hochtechnologischen Digitalzeitalter ein so relativ einfach überschaubarer Zusammenhang wie ein simples Kabel noch unergründete Geheimnisse bergen und darüber erhitzte Diskussionen auslösen kann? Recht hat er! In der Tat ist hier nicht den Gelehrten ein Versäumnis vorzuwerfen. Es gibt auch auf diesem Gebiet schwerlich etwas, worüber sich nicht schon jemand Gedanken gemacht und diese auch zu Papier gebracht hat, längst vor der Zeit, als die meisten, die dies lesen, geboren wurden.

Wenn man weiß, daß z.B. die in der jüngeren HiFi-Geschichte von der Audio-Ver- marktungsindustrie als vollständig neue Konzepte vorgestellten „Innovationen“ mit Namen „Moving Coil Prinzip“ oder „Reineisen-Magnetaufzeichnung“ in den Jahren 1898 bzw. 1899 patentiert wurden oder daß die Grundlagen zur korrekten Tonarmgeometrie im Jahr 1941 umfassend erarbeitet wurden und bis heute - teilweise auch bei renommierten Herstellern - noch nicht allgemeinen Eingang in die Fertigung gefunden haben, dann ist es auch gut vorstellbar, daß in diesen Tagen das Kabel mehrfach neu „erfunden“ wird.

 

Worin liegt der mangelnde Informationsstand begründet?

Vielleicht hat es in grober Unterschätzung der Kabeleinflüsse noch niemand für notwendig erachtet, die gesicherten Erkenntnisse aus der Leitungstheorie auf den uns interessierenden Audio-Bereich zu übertragen? Oder die Erkenntnisse sind mancherorts vorhanden und werden als Quasi-Geheimnisse gehütet und kultiviert? Wahrscheinlich ist dies jedoch vielmehr ein Musterbeispiel für die Bedeutung des vielzitierten „Transfers“ (dabei bewußt den Co-Ausdruck „Technologie“ vermeidend). In unserem Falle ist es Mangel an Erkenntnis-Transfer zwischen isoliert voneinander operierenden Fachbereichen. Den mit den höheren Weihen der Elektro- oder Nachrichtentechnik Versehenen mag das Kabelthema im HiFi-Bereich zu lapidar und nebensächlich, als hochstilisierte Spinnerei einiger Ausgeflippter Vorkommen. Ein Elektroingenieur fragte mich beim Anblick eines 2 x 2,5-qmm-Lautsprecherkabels lächelnd, ob ich denn da 10 Ampere drüberschicken wolle? Ich solle mir doch einmal die Schwingspulendrähte betrachten.

Vor wenigen Jahren „bewies“ ein Professor der Elektrotechnik mittels einer Aneinanderreihung von unangebrachten Vereinfachungen, daß unter normalen Raumbedingungen die Kabel immer zu kurz ausfielen, um irgendwelche negativen Auswirkungen im Audio-Frequenzbereich haben zu können, daß es darüber hinaus barer Unsinn sei, für Entfernungen unter 30 Meter stärkeres als etwa 2,5-qmm-Lautsprecherkabel zu verwenden. An Kabeln kürzer als 10 m seien auch mit den besten Meßmethoden kaum noch Unterschiede meßbar, und es seien absolut keine hörbaren Klangunterschiede festzustellen. Ganz „normale“ Kabel seien schlichtweg perfekt im Vergleich zu den anderen Gliedern der Wiedergabekette. Diesem Professor fehlten die vielgestaltigen Erfahrungen eines akribisch nach Klangverbesserung strebenden HiFi-Puristen. Er hätte seinen eigenen Worten (und Ohren) nicht geglaubt. Derartige Äußerungen von Fachleuten führten allerdings dazu, daß die Beschäftigung mit dem Thema „Kabel“ für sich seriös haltende Entwickler lange Zeit tabu war. Dagegen sind es im Audio-Bereich meist gerade Nichttechniker, die sich, ohne Scheuklappen und wenig um Konventionen kümmernd, auf von anderen ignorierten und belächelten Randgebieten bemühen, den widrigen Umständen ein Quentchen mehr Klangqualität zu entreißen.

Dieser Beitrag will aufzeigen, was an vorhandenen Erkenntnissen aus der Leitungstheorie konsequenterweise auf den uns interessierenden NF-Bereich angewandt werden sollte. Weil das Interesse am Kabel derzeit besonders groß ist, beschäftigen sich viele mit diesem Thema, wobei jedoch oft allzu schnell meist werbeträchtige Behauptungen aufgestellt werden, die sich nicht oder vielleicht noch nicht beweisen lassen. Um etwaigen falschen Erwartungen vorzubeugen, sei betont, daß solchen Vermutungen in diesem Beitrag bewußt nicht nachgegangen wird, mit Ausnahme derer, die widerlegbar sind.

 

 

Wie stellt man sich das ideale Kabel vor?

Die Umkehrung unserer Kardinalfrage nach dem (Un-) Wesen eines Kabels macht unser Problem leichter zugänglich, wenn man andersherum fragt: Wie muß ein ideales Kabel beschaffen sein? Die Antwort darauf fällt leichter und ist trivial einsichtig: Das ideale Kabel soll ein elektrisches Signal, das ihm am Eingang übergeben wurde, am Ausgang in unveränderter Form wieder abliefern. Der Zusatz „und Größe“, der einem aus dem täglichen Sprachgebrauch sofort auf der Zunge liegt, wirft jedoch bereits die erste Einschränkung auf.

 

Verfälschungen des Signals: Bedämpfung

Ein Kabel als passives Element (ausgenommen Supraleiter) wird physikalischen Grundgesetzen zufolge niemals ein Signal an seinem Ausgang mit gleicher Größe wie am Eingang präsentieren können. Man sagt, es ist verlustbehaftet. Diese Art von Verlust ist bei unseren kurzen Kabellängen im Wohnzimmer im Vergleich zu Überland-Fernmeldeeinrichtungen doch recht klein und würde uns zunächst nicht so wahnsinnig stören, da wir wissen, daß es Verstärker gibt. Doch eben weil es Verstärker gibt, müssen uns die Verluste stören, denn eine weitere Aufgabe eines Kabels ist es häufig, eine elektrische Größe an den Klemmen eines Gerätes an die Klemmen eines anderen quasi räumlich zu „transportieren“, weil sie dort zur korrekten Funktion gebraucht wird.

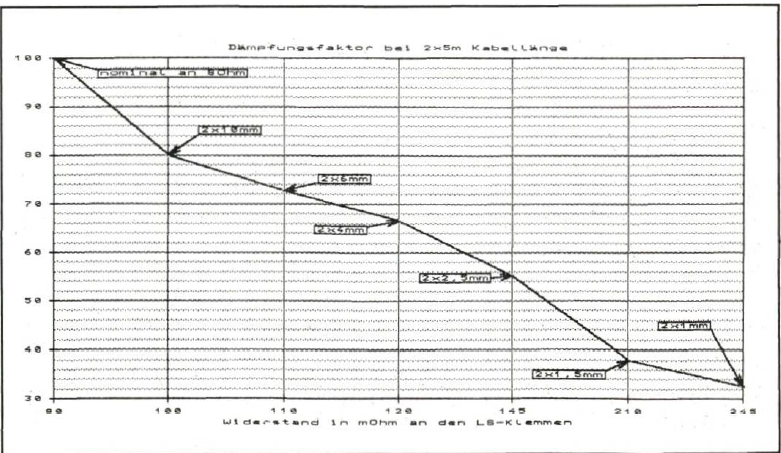
Dies ist beispielsweise die Niederohmigkeit eines Endstufenausganges, die zur Bedämpfung der exzessiven Membranbewegung eines Lautsprechers benötigt wird, oder die Kapazität eines Phonoeingan- ges, die zur Resonanzabstimmung eines Tonabnehmers beiträgt. Im Falle des Lautsprechers findet bei Vorhandensein eines größeren Leitungswiderstandes eine Bewertung der Klemmenspannung durch die Lautsprecherimpedanz statt, gemäß der Beziehung:

 

 

Da Verstärker üblicherweise für konstante Ausgangsspannung konzipiert sind, muß sich folglich die Spannung an den Klemmen der Lautsprecherbox und damit auch deren Amplitudenfrequenzgang ändern. Mit gutem Leitermaterial und großem Querschnitt, so weiß es heute jedes Kind, lassen sich die Verluste hinreichend niedrig halten. Falsch! - Man darf nicht vergessen, daß wir es mit Signalen im Tonfrequenzbereich zu tun haben, dessen untere und obere Grenzfrequenz sich immerhin um den Faktor 1000 unterscheiden.

 

 

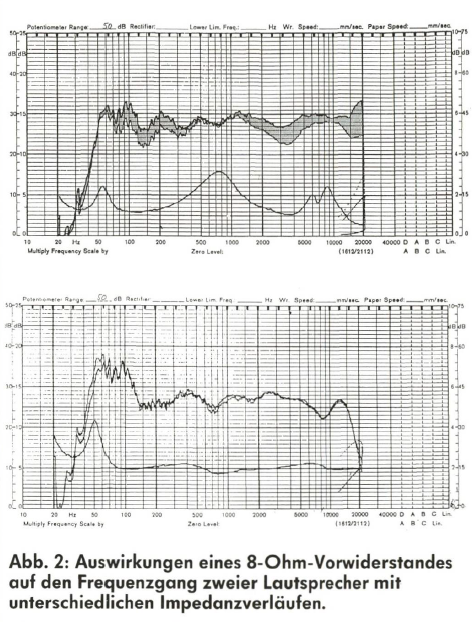
Leider behandeln die erwähnten unvermeidlichen Verluste unsere hochgeschätzten Frequenzen nicht alle mit derselben Meßlatte. Der Amplitudenfrequenzgang wird unlinear, sagt der Meßtechniker. Und was passiert in diesem Fall mit unserem Eingangssignal, das im Extremfall aus sämtlichen Frequenzen gleichzeitig besteht? Die Signalform am Ausgang muß sich zwangsläufig von der am Eingang unterscheiden, da sich die Form durch Überlagerung aller beinhalteten Sinusfrequenzen ergibt.

 

Phasenverschiebung

Nun, wenn wir schon einen Verstärker haben, dann werden sich doch diese läppischen nullkommaetwas dB mit dem Klangsteller ... Irrtum! Der frequenzabhängige Verlust - sprechen wir in der Folge lieber von Dämpfung - hat nach den Gesetzen der Elektrotechnik leider eine untrennbare und unliebsame Zwillingsschwester: die Phasenverschiebung (siehe auch: Grundlagen der HiFi-Technik V). Sie stellt sich als relative Verschiebung der beteiligten einzelnen Sinusfrequenzen in ihrer zeitlichen gegenseitigen Zuordnung dar, und zwar wiederum frequenzabhängig.

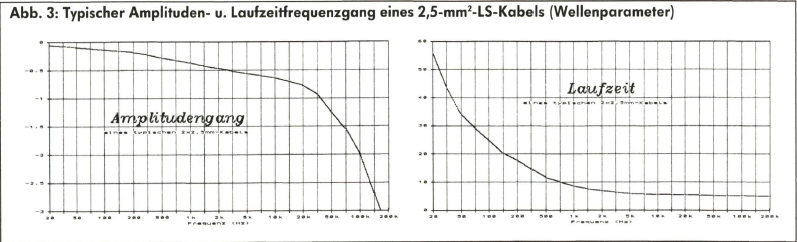
Und schon haben wir einen zweiten Grund, uns Sorgen über unsere Signalform zu machen, denn durch die Überlagerung der zeitlich verschobenen Frequenzanteile wird die ursprüngliche Signalform um ein weiteres Maß verfälscht. Noch deutlicher wird der schädliche Einfluß der Phasenverschiebung, wenn man von der stationären Betrachtungsweise überwechselt zur Impulsbetrachtung. Da eine Phasenverschiebung identisch mit einer zeitlichen Verschiebung ist, bedeutet dies auch, daß Signale verschiedener Frequenzen unterschiedliche Laufzeit vom Eingang des Kabels bis zum Ausgang haben und bei einem typischen 2 x 2,5-qmm-Kabel die hohen Frequenzen bis zu 10mal schneller sind als die tiefen (siehe Abb. 3).

Das zeitliche Muster jedoch, wie aus den Beiträgen zur Hörphysiologie bekannt, hat für das Ohr einen ganz wesentlichen Informationsgehalt. Diese zeitliche „Verschmierung“ (Dispersion) verursacht eine Verformung bei gleichzeitiger Verbreiterung von Rechtecksignalen, wodurch auch die Digitaltechnik nicht gegen Kabeleinflüsse immun bleibt. Ebenfalls wegen der Laufzeit sollen die beiden Kabel für Rechts und Links einer Stereoanlage gleiche Länge aufweisen, um Fehler bei der räumlichen Wiedergabe zu vermeiden. Unser Verstärker, als Amplituden-Frequenzgang-Kompensator eingesetzt, wäre unter Umständen noch in der Lage, die frequenzabhängige Dämpfung zu korrigieren, falls sich zufällig der reziproke Verlauf einstellen ließe, doch anstatt die Phasenverschiebung exakt rückgängig zu machen, würde er weitere Phasenverschiebungen hinzufügen. An dieser Stelle höre ich die Einwände: Was das Ganze wohl soll? Die nuilkomma etwas dB an Dämpfung und nullkomma etwas Grad an Phasenverschiebung seien bekanntermaßen sowieso nicht hörbar. Genau diese Art von Einwänden mag mit dazu beigetragen haben, daß erstaunlich wenig über Kabeleinflüsse im HiFi-Bereich exakt untersucht wurde. Ein einziges Gegenbeispiel - und davon gibt es mittlerweile etliche - sollte genügen, um diesen unsäglichen Kleinigkeiten die ihnen zustehende Aufmerksamkeit zu widmen.

 

Es gibt keine NF-Kabel!

Nach dem bisher Überlegten kann man die Forderung an ein Kabel mit den Worten des Nachrichtentechnikers neu formulieren:

Das ideale Kabel ist gekennzeichnet durch linearen Dämpfungsverlauf und konstante Laufzeit für alle Frequenzen des Übertragungsbereichs; es besitzt Allpaßcharakteristik und wird „verzerrungsfrei“ genannt. Kabel können für manche spezifischen Einsatzzwecke so hergestellt werden, daß sie diese Forderungen annähernd ganz ordentlich erfüllen. Aus ihrer Bezeichnung soll dann der optimale Einsatzzweck zu erkennen sein, z. B. HF-(Hochfrequenz-)Kabel. Sucht man nun unter diesem Gesichtspunkt nach NF(-Niederfrquenz-)Kabeln, so stellt man mit allergrößtem Erstaunen fest, daß die sogenannten NF-Kabel gar keine solchen sind. Betrachtet man sie genauer, dann entpuppen diese sich vielmehr als astreine HF-Kabel, so z.B. alle RG-Kabel-Typen. Ein Beweis hierfür ist auch, daß es Kabelanbieter gibt, die dasselbe Kabel für Audio und Video gleichermaßen anbieten; es unterscheidet sich höchstens noch durch den Aufdruck, die Farbe, die Stecker und den Preis. Die Ursache liegt wohl darin, daß fälschlicherweise angenommen wird, die Anforderungen an HF-Kabel seien schwieriger zu erfüllen und diese würden dadurch automatisch auch für NF-Zwecke gut sein.

Tatsache ist jedoch, daß sich Probleme - und dies läßt sich an ähnlichen Beispielen der Physik oder Elektrotechnik wiederholen - eher an den Bereichsgrenzen gravierend bemerkbar machen, siehe z. B. die Problematik (Baß- und Hochtonbereich) bei Tonabnehmersystemen, Mikrofonen und Lautsprecherboxen. Für Kabel sind diese Bereichsenden im UHF- und im NF-Bereich zu finden. Übrigens sind Lautsprecherkabel selbstverständlich auch NF-Kabel, was sonst? Eine Unterscheidung in NF- und LS- Kabel ist insofern begrifflich inkorrekt. Praktikabler wäre dagegen der Vorschlag, zwischen Kleinsignal-Kabel (KS-Kabel) und Großsignal-Kabel (GS-Kabel) für Niederfrequenz zu unterscheiden.

Nach der vorangegangenen, ernüchternden Feststellung, daß am Markt keine nach den Regeln der Kunst der Elektrotechnik speziellen NF-Kabel* angeboten werden, fragt man sich, falls man den inneren Drang zur Resignation überwunden hat, ob die schlechten Eigenschaften der Kabel schicksalhaft in Kauf genommen werden müssen oder ob es nicht doch Ansatzmöglichkeiten zu ihrer Eliminierung gibt. Dazu gilt es zunächst zu untersuchen, in welchen physikalisch-elektrischen Sachverhalten diese Unzulänglichkeiten begründet sind, woher also die Frequenzabhängigkeit rührt.

 

 

Effekte = Defekte

Daß der spezifische Widerstand des Leitermaterials eines Kabels zu einer Dämpfung führt, ist trivial einleuchtend. Nach Lehrbuch ist dieser spezifische Widerstand frequenzunabhängig und nur material- und temperaturbedingt. Der am Kabel gemessene elektrische Widerstand hängt darüber hinaus von der Länge und vom Querschnitt ab. - Und von der Frequenz! Nachdem eben der Widerstand schön frequenzunabhängig war, taucht hier plötzlich, scheinbar unmotiviert, die Frequenz auf. Bei solchen Anlässen spricht man gern von Phänomenen, von denen nach ihrer Erklärung nur noch Effekte bleiben. Das hier vermutete Phänomen ist erklärt, also nur noch Effekt, genauer gesagt:

 

Skin-Effekt

Der Skin-Effekt, auch bekannt als Heaviside-Effekt, ist nichts Neues. Doch stritt man ihm - in weiten Kreisen bis heute noch - leichtfertig und ungeprüft jegliche Bedeutung im NF-Bereich ab. Die Zusammenhänge sind seit langem ergründet und beschrieben: Innerhalb eines Leiters treten Stromkomponenten abweichend von der Hauptflußrichtung auf, sogenannte Wirbelströme, die sich dem Leiterstrom überlagern. Diese Wirbelströme sind die Ursache für eine resultierende Abnahme der Stromdichte zum Zentrum des Leiters hin, mit „Stromverdrängung“ bezeichnet. 

Weil die Wirbelströme durch Induktion hervorgerufen sind, ist dieses Verhalten zusätzlich noch frequenzabhängig, indem die Stromverdrängung mit zunehmender Frequenz stärker in Erscheinung tritt. Große Querschnitte erleichtern die Entstehung von Wirbelströmen. Daher ist es begreiflich, daß der Grad der Stromverdrängung vom Leiterquerschnitt abhängt. Diese Gesamterscheinung der Stromverdrängung bei zunehmendem Leiterquerschnitt und zunehmender Frequenz wird „Skin-Effekt“ genannt (von engl. Haut, Hülle, Oberfläche, da der Stromfluß quasi nur noch in einem gewissen Bereich dicht unter der Oberfläche konzentriert ist) und äußert sich in einer Widerstandszunahme, wie sie einer effektiven Querschnittsverminderung entspricht. Das Verhältnis R(f)/R0 mit R(f) = frequenzabhängiger Widerstand und Ro= Gleichstromwiderstand) wird als Skinfaktor bezeichnet.

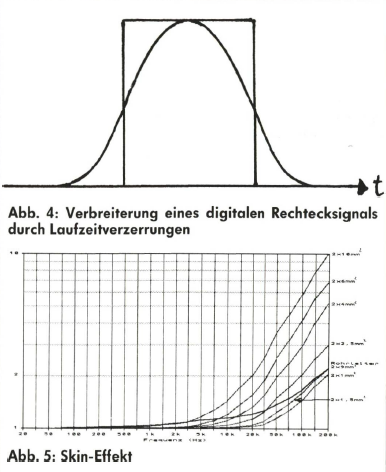
In Abb. 5 ist der Verlauf des Skinfaktors bei verschiedenen Kabelquerschnitten dargestellt. Es ist deutlich zu sehen, daß sich der Skin-Effekt bereits im Hörbereich auswirkt. Beim 2 x 10-qmm-Kabel steigt der Widerstand bei 20 kHz auf das Doppelte! Eine extreme Steigerung des Querschnitts (es sind Anwendungen von bis zu 2 x 180 qmm und mehr bekannt), wie sie von HiFi-Absolutisten in guter Absicht vorgenommen wird, schießt über das Ziel hinaus und schlägt ins Gegenteil um, wenn nicht spezielle Maßnahmen gegen den Skin- Effekt ergriffen werden. Die Grenzen des Sinnvollen liegen meines Erachtens bei etwa 2 x 6-qmm-Kabeln üblichen Aufbaus, was auch durch Klangerfahrungen bestätigt wird.

Zur Reduzierung des Skin-Effekts bieten sich zweierlei gehbare Wege an. Zum einen die Querschnittsverminderung im Baßbereich: Das Zentrum des Leiters, in dem bei hohen Frequenzen Stromverdrängung eintritt, wird einfach weggelassen, um gleiche Querschnittsbedingung auch für den Baß zu erzwingen. Es entsteht ein Leiter in Form eines „elektrisch hohlen“ Rohres. Das in Abb. 5 mit „Rohrleiter 2 x 9-qmm“ bezeichnete Kabel ist ein solcher Anwendungsfall.

Die Verwendung des Begriffs „Hohlleiter“ ist in diesem Zusammenhang jedoch Schlamperei, da im Tonfrequenzbereich nicht im Hohlen geleitet wird, im Gegensatz zur Mikrowellenleitung, wo der Begriff Hohlleiter definiert ist. Für die vorliegende Leiterform kann man vielmehr in der Fachliteratur die Ausdrücke „Oberflächen-“, „Hohlzylinder-“ oder „Rohrleiter“ finden. Der zweite mögliche Weg zur Verminderung des Skin-Effekts besteht darin, die Oberfläche zu vergrößern. Das alleinige Erhöhen der Drahtanzahl innerhalb einer Litze hat allerdings keinen Einfluß auf die elektrisch wirksame Oberfläche, obwohl in Prospekten gelegentlich das Gegenteil behauptet wird, was weder meßtechnisch beweisbar noch physikalisch einsichtig ist.

 

Erst durch Isolierung, z.B. mit einer Lackschicht, werden die für den Skin-Effekt ursächlichen Wirbelströme am Überqueren der Drähte gehindert. Ähnlich positiv  kann sich jedoch auch bereits eine Oberflächen-Oxydation der Drähte auswirken, die nicht nur bei Kontakt mit Sauerstoff aus der Luft, sondern auch durch Reaktion mit der Säure im Isoliermaterial im Laufe der Zeit eintreten kann.

 

Proximity-Effekt

auch Nähewirkung genannt. Dieser ist wohl den meisten aus einem einfachen Experiment im Physikunterricht bekannt: Eine lose herabhängende Drahtschleife öffnet sich bei Durchfließen von Strom. Parallele Leiter mit entgegengesetzt gerichteten Strömen stoßen sich ab. Im festvergossenen Kabel können sich die Leiter nicht wesentlich auseinander bewegen, also wird der Stromfluß innerhalb der Leiter zur äußeren Seite gedrängt, was sich ähnlich wie beim Skin-Effekt wie eine Querschnittsverminderung bzw. Widerstandserhöhung auswirkt. Es hat den Anschein, als ob damit konsequenterweise die Verwendung von im Abstand laufenden Leitungen, sogenannten Stegleitungen, auf der Hand läge. Doch wie bald gezeigt wird, wäre mit einem geringfügigen Vorteil ein schwerer wiegender Nachteil für die Kabeleigenschaften erkauft.

 

Die Entmystifizierung des Kabels

 

Beim letztem Mal beleuchteten wir einige primäre Ursachen für das mangelhafte Frequenzverhalten von realen Kabeln. Nachfolgend sollen nun die elektrischen Grundbausteine einer Leitung beschrieben werden, um daraus Aussagemöglichkeiten für das Übertragungsverhalten zu beziehen.

 

Leitungsparameter

Der einfachste, aber auch unvermeidlichste und zahlenmäßig größte Parameter wurde bereits mehrmals genannt: Der Widerstand R; Benennung Ohm. Er wirkt in Längsrichtung (seriell zur Last) und wird bei am Ende kurzgeschlossener Leitung von der Eingangsseite her gemessen, so wie er sich an den Klemmen eines Geräteausgangs zur Last addiert. Das heißt, der Widerstand wirkt in der Hin- und Rückleitung und ist so groß wie die Summe der Widerstände der einzelnen Leiter; er wird bei dieser Betrachtung Schleifenwiderstand genannt.

Einige Kabelanbieter geben jedoch in bewußter Irreführung des Kunden nur den Widerstand eines Leiters an, um bei Prospektvergleichen besonders niedrige Werte vorzutäuschen. Sie wissen dabei sehr wohl, daß der Laie die niedrigen Leitungswiderstände mit einfachen Ohmmetern kaum reproduzierbar nachmessen kann - es sei denn bei entsprechend großen Längen, weil die Meßauflösung, der Widerstand der Meßleitung und der Kontaktübergangswiderstand bereits in der Größenordnung des zu messenden Wertes liegen. Überdies ist der Widerstand auch noch temperaturabhängig und sollte bei 20 Grad Celsius angegeben werden. Eine Temperaturabweichung von ± 10 °C bewirkt bei Kupfer eine Widerstandsänderung von etwa 4 Prozent.

Der Widerstand ist wie alle anderen Leitungsparameter frequenzabhängig (Abbildung 6, siehe auch Skin-Effekt). Die zu messenden Gleichstrom- Schleifen widerstandswerte bewegen sich von unter 5 bis zu einigen -zig Milliohm bei Lautsprecherkabeln, beziehungsweise biszu einigen hundert Milliohm bei Kleinsignalkabeln pro Meter. Der auf die Einheitslänge bezogene Widerstandwert wird als Widerstandsbelag bezeichnet und mit dem gestrichenen Symbol R' (Benennnung: Ohm/m) abgekürzt. In der Fernmeldetechnik beziehen sich die Beläge der Leitungsparameter auf die Einheitslänge 1 km, während wir hier die Einheitslänge von 1 m wählen.

 

 

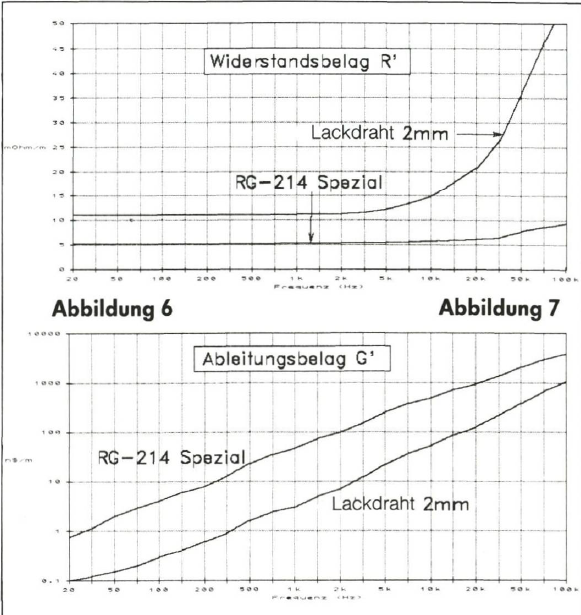
Eng verwandt mit dem Widerstand ist die Ableitung G. Sie ist der Kehrwert des zwischen Hin- und Rückleitung eines Kabels wirksamen Querwiderstandes (parallel zur Last). Dieser resultiert aus einem endlichen Isolationswiderstand und dielektrischen Verlusten durch Aufladung des Isoliermaterials. Gemessen wird die Ableitung bei leerlaufendem (offenem) Leitungsende; die Benennung ist 1/Ohm = S (Siemens).

Von allen Leitungsparametern ist die Ableitung weitaus am stärksten frequenzabhängig: Verhältnisse von 1:1000 und mehr zwischen 20 Hz und 20 kHz sind üblich (Abb. 7).

Der Frequenzverlauf ist nahezu exponentiell. Dennoch ist die Ableitung bei Kabeln unter Verwendung moderner Isoliermaterialien oft so niedrig, daß sie nur mit allergrößten Schwierigkeiten meßtechnisch einwandfrei bestimmt werden kann, so z.B. beim RG 214 oder Postkabel liKx. Sie ist auch stärker temperaturabhängig als der Längswiderstand (eine Temperaturabweichung von ±10°C kann eine Änderung der Ableitung von bis zu 60 Prozent bewirken!) und darüber hinaus auch von mechanischen Beanspruchungen, wie Druck durch Biegen. Knicken oder Quetschen, beeinflußt. Der Ableitungsbelag wird mit G' (Benennung: S/m) abgekürzt und bewegt sich normalerweise in der Größenordnung pS/m bis weniger als nS/m, was einem Isolationswiderstand von Megaohm biszu mehreren Gigaohm mal Meter entspricht.

Diese geringe Größe der Ableitung verleitet jedoch dazu, sie häufig bei theoretischen Betrachtungen der Einfachheit halber gleich Null zu setzen - ein folgenschwerer Fehler: Da wires bei der Realisierung von Kabeln immer mit verlustbehafteten Leitungen zu tun haben, ist - wie später noch gezeigt werden wird - ohne Einbeziehung der Ableitung in die Betrachtung die angestrebte verzerrungsfreie Leitung im NF-Bereich nicht zu verwirklichen. Die bedingte oder künstliche Erhöhung der Ableitung erweist sich im Gegenteil sogar als praktikables Mittel, ein nicht perfektes Kabel zu optimieren.

Die Induktivität L hat ihre Ursache im Fließen von Strom innerhalb eines Magnetfeldes. Es wird zunächst vom Stromfluß in der Hin- und Rückleitung eines Kabels selbst verursacht, abhängig hauptsächlich von der geometrischen Anordnung der Leiter zueinander und der daraus resultierenden Wechselwirkung. Doch auch fremde äußere Magnetfelder, in erster Linie das Erdmagnetfeld oder Streufelder von Leitungsnetzen, Netzteilen, Motoren sowie das Vorhandensein von magnetisierbaren Materialien wie Eisenträgern, verstärken die Induktivität. Sie wird also durch Wechselwirkung im Raum außerhalb des stromführenden Leiters verursacht und deshalb als äußere Induktivität bezeichnet.

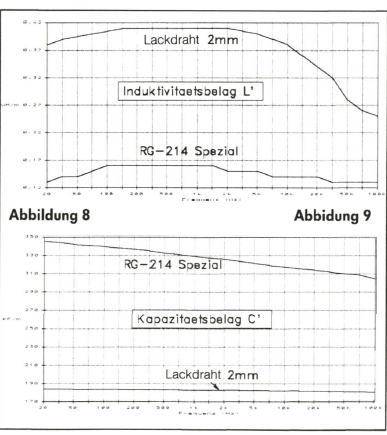
Aber auch im Leiterinneren existiert ein Magnetfeld, primäre Ursache für Wirbelströme, die auch den Skin-Effekt bewirken, dessen Folge die sogenannte innere Induktivität ist. Bei Kabeln mit ausgeprägtem Skin-Effekt nimmt deshalb, infolge des Anteils der inneren Induktivität an der Gesamtinduktivität, bei höheren Frequenzen die Induktivität wieder ab (vergleiche Abb. 6 und 8).

Die Induktivität wird, ebenso wie der Widerstand, bei kurzgeschlossenem Leitungsende bestimmt und entsprechend der seriellen Wirkungsweise auch Längsinduktivität genannt. Sie kann deshalb auch in der Messung gemeinsam mit dem Widerstand ermittelt werden, da sie zum imaginären oder reaktiven beziehungsweise Blindanteil an der Kurzschlußimpedanz beiträgt, wogegen der Widerstand den reellen oder Wirkanteil verkörpert: 

 

 

wobei die Induktivität mit L bezeichnet wird und die Bezeichnung H (Henry) hat. Der bei Kabeln meßbare Induktivitätsbelag L’ bewegt sich im Bereich von 0,1 /m bis über 1 /m und ist dabei deutlich weniger frequenzabhängig als der Widerstandsoder der Ableitungsbelag (Abb. 8). Im wesentlichen bestimmen die geometrische Form und Lage der beiden Leiter zueinander die Induktivität. Durch Verdrillen läßt sich der Induktivitätsbelag verringern, wogegen er sich durch Vergrößern des Leiterabstandes erhöht. Die erreichbare, theoretisch mögliche untere Grenze ist durch die innere Induktivität mit 0,05 /m vorgegeben.

Der letzte Leitungsparameter schließlich ist die Kapazität C. Im Gegensatz zur Induktivität hat die Kapazität ihre Ursache nicht in einem elektromagnetischen, sondern in einem elektrostatischen Feld, das durch die Polaritätsdifferenz der beiden Leiter hervorgerufen wird und deshalb auch ohne Stromfluß vorhanden ist. Sie wird wie die Ableitung bei offenem Leitungsende gemessen und ihrer Wirkungsweise zufolge auch Parallelkapazität genannt. Durch Messung der Leerlauf- admittanz kann die Kapazität daher gleichzeitig mit der Ableitung bestimmt werden und trägt zum imaginären oder Blindanteil an der Gesamtadmittanz bei: 

 

 

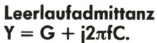
Die Benennung der Kapazität C ist F (Farad), und F/m ist die des Kapazitätsbelags C’. Praktische Meßwerte des Kapazitätsbelags liegen üblicherweise in der Größenordnung pF/m bis nF/m (Abb. 9). Ebenso wie die Ableitung ist die Kapazität außer von der Frequenz auch von der Temperatur und der mechanischen Beanspruchung des Kabels abhängig. Maßgebend für die Größe der Kapazität ist wiederum die Geometrie der Leitungen und ihre Anordnung zueinander und außerdem die relative Dielektrizitätskonstante des dazwischen befindlichen Isoliermaterials. Dabei ist die Kapazität um so höher, je größer die einander gegenüberliegende Leiteroberfläche, je kleiner der Abstand dieser Flächen zueinander und je größer die relative Dielektrizitätskonstante er des Zwischenmediums, ist. Für Koaxialkabel gilt zum Beispiel:

 

 

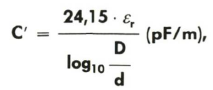
mit d = Außendurchmesser des Innenleiters und D = Innendurchmesser der Abschirmung. Auch für die Kapazität gibt es ein theoretisch nicht zu unterschreitendes Minimum von ca. 7 pF/m, da jeder Leiter gegenüber Erde eine Kapazität aufweist.

Ein Vergleich mit der Induktivität zeigt, daß die einflußnehmenden Kriterien bei der Kapazität genau gegenläufig sind: Vergrößern des Leiterabstandes verringert die Kapazität und erhöht die Induktivität. Das bedeutet allgemein, daß Maßnahmen zur Reduzierung bei Kapazität und Induktivität reziproke Wirkung zeigen. Bei hinreichend hohen Frequenzen gilt sogar strenggenommen: Das Produkt aus Induktivität mal Kapazität ist konstant.

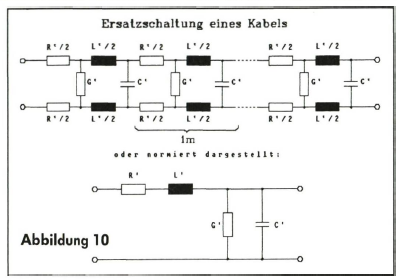
Zusammenfassend läßt sich nun mit Hilfe der Leitungsbeläge das in Abb. 10 gezeigte Ersatzschaltbild einer Leitung aufzeichnen. Besonders sei betont, daß die Ersatzschaltung nur ein Vorstellungsmodell ist: Seine Elemente darf man nicht als reale Bauteile eines Netzwerkes auffassen. Das Arbeiten mit einem Modell ist in der Physik üblich und so lange zulässig, als die mit seiner Hilfe hergeleiteten Aussagen mit übergeordneten anderen Betrachtungsweisen und Methoden harmonisieren und keine Widersprüche auftreten. So sind zum Beispiel die aus den Leitungsparametern gewonnenen Aussagen über die Amplitudendämpfung oder die Laufzeit identisch mit dem Ergebnis aus aufwendigen Direktmessungen. Auch wegen der mehr oder minder deutlichen Frequenzabhängigkeit der Leitungsparameter können die Elemente des Ersatzschaltbildes nicht als für alle Frequenzen geltende Bauteile gesehen werden: Für jede Frequenz wären andere Werte notwendig. Ebenfalls aus diesem Grund sind übliche Prospektangaben irgendeines Parameters, gewöhnlich bei 1 kHz gemessen, unbrauchbar und können höchstens einer oberflächlichen Trendaussage dienen. 

 

 

Die anerkannte Leitungstheorie beweist den Grundsatz:

Die vier Leitungsparameter Widerstand, Ableitung, Induktivität und Kapazität bestimmen das elektrische Verhalten einer Übertragungsleit. Sämtliche Aussagen über das Übertragungsverhalten von Kabeln sind aus den Leitungsparametern ableitbar.

Dieser Grundsatz der Leitungstheorie klingt in seiner Einfachheit und Pauschalität wie Hohn für die vielen hochtrabenden „Philosophien“ und stellt sie teilweise in Frage. Gleichzeitig birgt er doch die Hoffnung, das „richtige“ Kabel high-endlich zu finden.

 

Welcher Leitungsparameter ist der „Drahtzieher" des Mißklangs?

Bei der kriminalistischen Suche nach den klanglichen Missetätern konnte also bis hierher der Kreis der Verdächtigen auf vier handelnde Parameter eingegrenzt werden. Doch welcher von diesen ist nun der schlimmste Unhold und sollte als Feind Nr. 1 bekämpft werden?

Nachdem in der HiFi-Kabelszene der vergangenen Jahre zuerst der Gleichstromwiderstand mit wahrlichen Kupferbergwerken bekämpft wurde, der Widerstand daraufhin in den Untergrund ging und dennoch die erhofften klangfriedlichen Kabelzeiten nicht anbrachen, zog die Kapazität den Unmut des Publikums auf sich. Mit überdimensionalen Stegleitungen, Koaxialkabeln großen Außendurchmessers und modernsten Dielektrika bis hin zur reinsten deutschen Industrieluft wurde die Kapazität in die Ecke getrieben und niedergemacht. Erstaunt stellte man jedoch fest, daß paradiesische Kabelklangzustände noch in ebenso weiter Ferne waren wie vorher - lediglich die Verwirrung war größer.

Hatte man etwas übersehen? Da muß also doch etwas dran sein am Gerede um den Skin-Effekt? Oder liegts am Kupfer: OFC oder LC-OFHC oder HOCOPOCUS? - Die Induktivität! Die muß schuld sein am Kabelklangdesaster! Also wird ihr mit vielfach überkreuz gemoppelter unlösbarer Spezialverseilung auf den Leib gerückt. Doch oh weh! Die mühsam gebändigte Kapazität nutzt die Gelegenheit und bläht sich wieder bedrohlich auf. - Großes Rätselraten!

Spätestens zu diesem Zeitpunkt müßte jeder Hobbydetektiv kombinieren, daß es sich bei den Leitungsparametern nur um einen Fall von bestens organisiertem Bandenunwesen mit genau verteilten Zuständigkeiten handeln kann: Jeder einzelne Parameter trägt seinen Teil zum Miß oder Gelingen der gestellten Aufgabe bei. Keiner ist wichtiger oder unwichtiger als ein anderer. Unsere Forderung an das ideale Kabel in Erinnerung, sollte es uns nur interessieren, in welcher Weise das Zusammenwirken aller Leitungsparameter das Amplituden- und Laufzeitverhalten eines Kabels prägt. Die Leitungstheorie liefert die Antwort.

 

Alles unter einem Hut

Sieht man das zu übertragende Signal als Aneinanderreihung von Momentanwerten der Spannung am Eingang des Kabels, dann ist der ganze komplexe Kabelfluß in einem Faktor zusammengefaßt vorstellbar, dessen Multiplikation mit der Eingangsspannung Ue die Ausgangsspannung Ua ergibt:

 

 

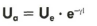
Im Übertragungsfaktor e-yl steckt der komplette, jedoch vom Betriebszustand isolierte Kabeleinfluß, das heißt ohne Berücksichtigung des rückwirkenden Einflusses vor- oder nachgeschalteter Komponenten. Der Fachmann spricht vom Wellenzustand des Kabels: Man betrachtet einen Teilausschnitt einer fortschreitenden Welle, so als ob das Kabel nach beiden Seiten unendlich verlängert wäre. Die Exponentialfunktion bringt zum Ausdruck, daß Spannung und Strom innerhalb eines Kabels mit zunehmender Entfernung vom Eingang nicht linear, sondern exponentiell (gemäß der natürlichen Degression: zuerst schnell und dann immer langsamer) abnehmen. Das negative Vorzeichen des Exponenten verkörpert die Abnahme, und 1 (für Länge) besagt, daß die Gesamtwirkung von der Kabellänge 1 abhängt.

Y wird als Übertragungskoeffizient bezeichnet, der wegen des 1 in obiger Formel wie die Leitungsparameter auf die Einheitslänge bezogen ist. Er ist eine für jedes Kabel charakteristische komplexe Größe und läßt sich in Real- und Imaginärteil zerlegen:

 

 

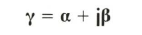
In diesem komplexen Ausdruck ist a der Real- oder Wirkanteil, der die Signaldämpfung verursacht, ß als Imaginär- oder Blindanteil ist schuld an der Phasenverschiebung. j stellt die imaginäre Einheit dar.

Und schon haben wir unsere lange gesuchten Schlüsselkriterien für das Übertragungsverhalten eines Kabels gefunden. a ist der Dämpfungsbelag, und ß wird Phasenbelag genannt - beide auf die Einheitslänge bezogen, a kennzeichnet die relative Amplitudenabnahme je Einheitslänge und kann sich zwischen 0 und 1 bewegen. Es gilt

 

 

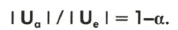
Bei gängigen Kabeln ist der Dämpfungsbelag im NF-Bereich frequenzabhängig und nimmt mit der Frequenz zu. Mit der Kenntnis von a läßt sich nun der Amplitudenfrequenzgang mittels 20 log (1-a) in dB/m aufzeichnen (Abb. 11). Der Phasenbelag ß hat die Benennung Radian/m und drückt die frequenzabhängige Phasendrehung pro Einheitslänge aus. Aus dem Phasenbelag berechnet sich die Geschwindigkeit, mit der sich ein Phasenzustand fortplanzt, die Phasengeschwindigkeit. 

 

 

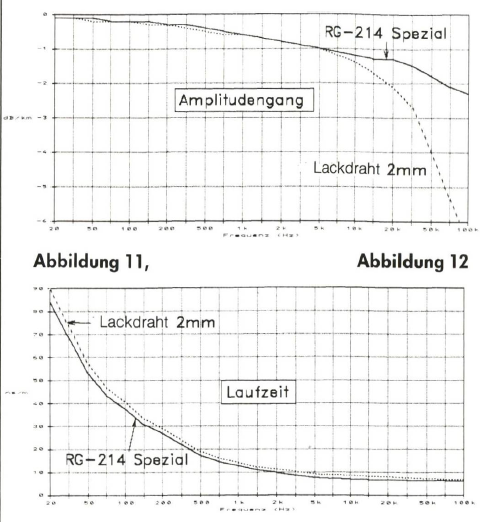
Nun stellt sich nur noch die Frage, wie man aus den bekannten Leitungsparametern a und ß erhält. Die Differentialrechnung liefert die Ergebnisse:

 

 

Erinnert sei nochmals daran, daß a und ß das Wellenverhalten eines Kabels beschreiben und daher auch Wellenparameter heißen. Sie alleine geben jedoch noch keinen letztendlichen Aufschluß über die Signalübertragung zwischen zwei Komponenten, die mit diesem Kabel zu verbinden sind. Ein weiterer Wellenparameter muß noch hinzugezogen und die ein- und ausgangsseitigen Geräte berücksichtigt werden.

 

Die Entmystifizierung des Kabels

3. Das Rezept

Bisher wurde gezeigt, daß die vier Leitungsparameter Widerstandsbelag R’, Ableitungsbelag G’, Induktivitätsbelag L’ und Kapazitätsbelag C das Ubertragungsverhalten eines Kabels vollkommen bestimmen, bei Berücksichtigung seines Frequenz- und Temperaturverhaltens und gleichzeitiger Erfüllung der Bedingungen: Homogenität des Kabels, kurze Meßlänge sowie Spannungs- und Stromunabhängigkeit der Parameter. Der Zusammenhang zwischen den Leitungsbelägen und dem Dämpfungsund Phasenverhalten eines Kabels wurde formelmäßig dargestellt.

Doch was hat der nach einer klanglich und meßtechnisch einwandfreien Kabellösung Suchende bisher gewonnen? Er kann lediglich an Hand der gemessenen Parameter die mangelhaften Eigenschaften von HiFi-Kabeln feststellen. Welchen Weg zur Verbesserung sollte jedoch ein Entwickler einschlagen? Die Formeln für den Dämpfungsbelag a und den Phasenbelag ß sind ziemlich unübersichtlich und daher auf Anhieb nicht so sehr geeignet, um festzulegen welcher Parameter in welcher Weise zur Optimierung eines Kabels gezielt verändert werden sollte.

 

Die verzerrungsfreie Leitung

Um einen neuen Ansatz in diese Richtung zu machen, betrachten wir eingehend die elektrische Wirkungsweise von Induktivität und Kapazität: Die Induktivität wirkt wie ein frequenzabhängiger Widerstand, der mit der Frequenz ansteigt, bei damit verbundener Phasennacheilung des Stromes gegenüber der Spannung von 90°. Bei der Kapazität ist die Wirkung umgekehrt, indem dieser Widerstand bei tiefen Frequenzen zunächst groß ist und nach hohen Frequenzen hin abnimmt, bei gleichzeitiger 90° - Phasenvoreilung des Stromes gegenüber der Spannung.

Diese gegenläufigen Eigenschaften von Induktivität und Kapazität deuten die verlockende Möglichkeit an, beide gegeneinander auszuspielen. Man müßte jetzt nur dafür sorgen, daß Induktivität und Kapazität exakt spiegelbildliche Blindwiderstandskurven erzeugen, dann würden sie sich bei Addition zu einer reellen Widerstandsgeraden kompensieren, und die Phasenverschiebung des Stromes wäre Null.

Dies ist so einfach allerdings nur bei real nicht existierenden reinen Induktivitäten und Kapazitäten möglich. Bei unseren Kabeln bewirken der Widerstand R und die Ableitung G Abweichungen vom idealen Verhalten, die mit Verlusten beschrieben werden. In der komplexen Zahlcnebene, wo der Elektrotechniker mit großem Vorteil operiert, um komplizierte Zusammenhänge leichter zu überblicken, lassen sich diese Verluste als Winkel darstellen; man spricht dann bildlich von Verlustwinkeln. Die induktiven und kapazitiven Verlustwinkel in unserer Leitungs-Ersatzschaltung ergeben sich..

Die reaktiven Wirkungen von Induktivität und Kapazität heben sich gegenseitig auf, wenn deren Verlustwinkel gleich groß sind. Wenn dies für alle Frequenzen zutrifft, dann ist der Dämpfungsbelag a linear und der Phasenbelag ß ist proportional zur Frequenz, die Laufzeit also ebenfalls linear. Damit sind unsere Forderungen an das ideale Kabel erfüllt, und das Rezept für die verzerrungsfreie Leitung wurde gefunden, indem für alle zu übertragenden Frequenzen gelten muß: 

 

R/L = G/C

 

Diese einfache Bedingung ist jetzt allerdings keine neue Entdeckung, sondern sie wurde bereits 1890, von dem englischen Privatgelehrten Oliver Heaviside formuliert, einem Neffen des berühmten Wheatestone. Heaviside entdeckte unter anderem den im Teil 1 behandelten Skin-Effekt. Die obige Bedingung wird nach ihm auch „Heavisidesche Relation" genannt.

Durch probeweises Einsetzen einiger Zahlenwerte aus den Parameterkurven unserer Beispielkabel (Bild 6 bis 9) ist schnell zu finden, daß die verzerrungsfreie Bedingung bei herkömmlichen sogenannten NF-Kabeln bei tiefen und mittleren Frequenzen weit verfehlt wird. Warum nur wurde bei HiFi-Kabeln die in Fachkreisen bekannte Bedingung für die verzerrungsfreie Leitung in der Vergangenheit mißachtet und wurden stattdessen zweifelhafte Philosophien konstruiert? Hier bewahrheitet sich offensichtlich eine alte chinesische Weisheit: „Zu wissen, wie man etwas macht, ist nicht schwer. Schwer ist nur, es zu machen."

Dabei haben Pupin 1900 und Kramp 1902 je einen möglichen Weg beschrieben, die verzerrungsfreie Leitung zu verwirklichen. Vor allem der Vorschlag Pupins, die Induktivität mittels in festen Abständen in die Leitung zwischengeschalteter Spulen zu erhöhen, konnte sich bei Fernmeldeleitungen durchsetzen, wogegen die Empfehlung Krarups, dasselbe durch Umwickeln der Leitung mit Eisendraht zu erreichen, vermutlich aus Kostengründen keine große Bedeutung erlangte, obwohl sie vom Standpunkt der Homogenität konsequenter war.

Betrachtet man die Leitungsparameter unter dem neuen, jetzt einfach erscheinenden Gesichtspunkt der Erfüllung der „Heaviside-Rela- tion“, so wird sofort klar, daß die Ableitung G bei bekannten „NF-Kabeln“ praktisch immer zu klein ist, und daß deren Vernachlässigung zu Null die verzerrungsfreie Leitung in der Realität sogar unmöglich macht; es müßte der Widerstand R ansonsten ebenfalls verschwinden oder die Induktivität unendlich groß werden, was beides nicht möglich ist. Bei HF-Kabeln ist die Heaviside-Relation tatsächlich in einem weiten Frequenzbereich erfüllt, da dort die Ableitung stark ansteigt.

Durch Überprüfen stellt man also schnell fest, daß bei üblichen HiFi-Kabeln R/L immer größer als G/C ist. Um dies zu beheben, müßte in der Gleichung links R kleiner und L größer, sowie rechts G größer und C kleiner gemacht werden. Es erscheint also durchaus mühelos genügend Spielraum vorhanden zu sein, um jedes beliebige Kabel noch verzerrungsfrei zu bekommen - einmal von der Schwierigkeit abgesehen, dies frequenzunabhängig zu bewerkstelligen. Doch ein bis jetzt noch nicht berücksichtigter, zur Beurteilung der Kabeleigenschaften äußerst wichtiger, charakteristischer Parameter schränkt den Spielraum für Manipulationen drastisch ein. Diesen zu kennen und zu kontrollieren, ist unabdingbar, damit die verzerrungsfreie Leitung überhaupt voll wirksam werden kann:

 

Der Wellenwiderstand.

Was hat es mit dem Wellenwiderstand auf sich? Wohl jeder weiß, daß man für Fernsehantennenzuleitungen heute 75--Kabel (früher 240--Kabel) verwendet. An vielen Tunern finden sich wahlweise zu benutzende Antenneneingänge mit den Bezeichnungen 75  und 300 . Würde man die 75 mit dem Ohmmeter aus dem Antennenkabel herausmessen wollen, so wäre dem wenig Erfolg beschieden. Der Wellenwiderstand kann doch nur etwas für HF-Techniker sein und ist im Audio-Frequenzbereich vollkommen unwichtig? Diese Meinung ist auch unter sogenannten HiFi-Spezialisten leider weit verbreitet. Der Wellenwiderstand erleidet in dieser Hinsicht die gleiche Mißachtung wie der Skin-Effekt, obwohl er eine der wichtigsten, wenn nicht die wichtigste Leitungskenngröße überhaupt ist.

Aber was für ein rätselhafter Widerstand kann der Wellenwiderstand sein? Haben wir den Widerstand als Leitungsparameter nicht schon ausgiebig genug behandelt? Um die weitverbreitete Fehleinschätzung des Wellenwiderstandes zu revidieren, ist es an dieser Stelle notwendig, ausführlich auf sein Wesen einzugehen. Die Ursache für die mangelnde Bewertung des Wellenwiderstandes liegt sicherlich auch darin, daß er sich einer vordergründig einfachen Vorstellung entzieht - er ist ja nicht einmal mit einem üblichen Meßgerät direkt abzulesen.

Dem Ohmschen Gesetz zufolge drückt der Widerstand das Verhältnis von Spannung zu Strom aus, beispielsweise am Eingang einer Schaltung. Beim Kabel kann man ebenso ein Spannung/Strom-Verhältnis am Eingang bestimmen, doch hängt dieses außer von den Leitungselementen in hohem Maße vom Lastwiderstand am Ende des Kabels ab. Zur Widerstandscharakterisierung eines Kabels sollten jedoch sinnvollerweise nur Werte herangezogen werden, die vom Kabel allein bestimmt werden. Der Widerstand, von dem hier die Rede ist, darf nicht verwechselt werden mit dem bereits eingehend beschriebenen Widerstandsbelag einer Leitung. Jener ist nur ein Bestandteil der gesamten Leitung, während wir jetzt von dem Widerstand als Hindernis reden, das ein Kabel der Fortpflanzung eines Signalzustandes entgegensetzt, und hierbei spielt der Kabelaufbau als Ganzes eine Rolle.

Um beim Kabel ohne Last einen Eingangswiderstand zu bestimmen, gibt es nur zwei eindeutige Zustände, von denen jeder ein Verhältnis von Spannung zu Strom prägt: die Kurzschlußimpedanz Zk und die Leerlaufimpedanz Z,. (Die Leerlaufimpedanz ist der Kehrwert der zur Bestimmung der Leitungsparameter verwendeten Leerlaufadmittanz.) Der gesuchte Wellenwiderstand ist nun gegeben durch das geometrische Mittel aus beiden Impedanzen:

 

 

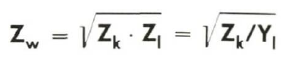
Auch der Wellenwiderstand stellt wiederum ein Spannung/Strom-Verhältnis dar, und zwar bezogen nur auf jede Teilwelle, aus der eine fortschreitende Welle besteht, womit die Bezeichnung Widerstand ihre Berechtigung gefunden hat. Im Gegensatz zum Leitungswiderstand ist der Wellenwiderstand an jeder Stelle einer homogenen Leitung gleich groß und somit längenunabhängig.

Im übrigen setzt jedes Fortpflanzungsmedium dem fortzupflanzenden Zustand einen dem Wellenwiderstand analogen Widerstand entgegen. So gilt zum Beispiel für die Fortpflanzung einer elektromagnetischen Welle (Radiowelle) im Vakuum ein Wellenwiderstand von 

 

 

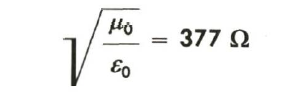
Wie wir bereits wissen, sind Kurzschluß- und Leerlaufimpedanz komplex und obigem Ausdruck zufolge damit auch der Wellenwiderstand; das bedeutet, man kann ihn durch Real- und Imaginärteil oder Betrag und Phase ausdrücken. Der Betrag des Wellenwiderstandes interessiert uns für die weiteren Betrachtungen ganz besonders. Wir gewinnen ihn aus obigem Ausdruck mit: 

 

 

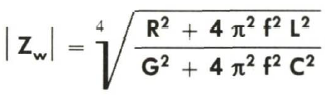
Diese Formel ist eine weitere Bestätigung dafür, daß aus den Leitungsparametern allein alle Leitungseigenschaften herleitbar sind.

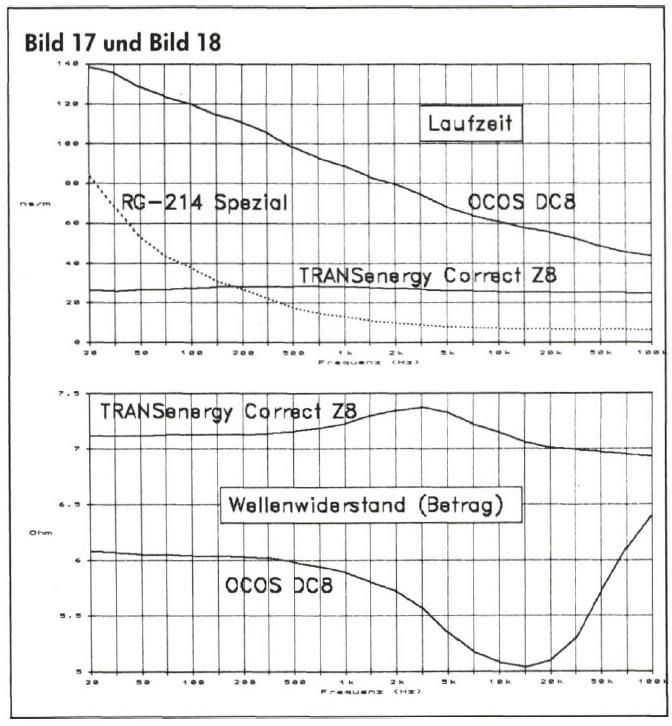
Berechnen wir den Wellenwiderstand für unsere Beispielkabel, so fällt sofort die starke Frequenzabhängigkeit bei mittleren und tiefen Frequenzen auf (Bild 13). Außerdem liegen die Wellenwiderstände mit ihrem linearen Bereich unterschiedlich hoch (hier von 20 über zirka 40 bis 115 Ohm). Noch ist nicht geklärt, warum der Wellenwiderstand so wichtig sein soll, haben wir doch gesagt, daß der Dämpfungsbelag a und der Phasenbelag ß die Signalbeeinflussung durch das Kabel erschöpfend beschreiben. Dies ist auch richtig, denn es wurde dabei vom Wellenzustand des Kabels gesprochen, bei dem das Kabel unendlich lang angenommen wurde. Für den wirklichen Kabeleinsatz, ganz besonders bei den kurzen Lösungen im Wohn- raum, entspricht dieser Zustand ganz selbstverständlich nicht der Realität. Das Kabel soll schließlich irgendwelche Komponenten verbinden, um einen Signaltransport zu bewerkstelligen. Es wird dabei zwangsläufig am Ende mit einer gegebenen Lastimpedanz abgeschlossen.

Was bedeutet diese veränderte Situation für das Signal, das sich zunächst unter vom Wellenwiderstand geprägten Bedingungen im Medium Kabel fortpflanzt? Es wird, am Ende angelangt, feststellen müssen, daß ein neues Medium mit veränderten Fortpflanzungsbedingungen beginnt. Aus der Physik wissen wir, daß bei analogen Fällen des Übergangs von einem Medium in ein anderes Brechung und Reflexion stattfinden. Beispiele hierfür sind die Lichtbrechung und -reflexion an der Wasseroberfläche oder an Temperaturgrenzen in der Luft (Luftspiegelung), aber auch die in diesem Forum geläufigeren Schallreflexionen sind durch Mediumübergang verursacht. Die Reflexion entspricht beim Kabel einer Richtungsänderung des Signals und die Brechung einer Phasenverschiebung.

 

 

Elektrisch ist die Reflexion dadurch zu erklären, daß durch den Abschlußwiderstand am Ende des Kabels ein Spannung/Strom-Verhältnis erzwungen wird, das von dem abweicht, welches durch den Wellenwiderstand gegeben ist. Die Energiebilanz kann nur dadurch aufrechterhalten werden, indem ein Teil der Energie wieder zurück zum Eingang geschickt wird. Es tritt dann zusätzlich zur hinlaufenden Welle eine rücklaufende Welle auf, für die wiederum die gleichen Fortpflanzungsbedingungen gelten, also Spannung/Strom-Verhältnis gemäß Wellenwiderstand. Durch Überlagerung beider Wellen ergibt sich ein vom Wellenwiderstand abweichendes Spannung/-Strom-Verhältnis, nämlich das, das man durch direkte Messung ermitteln kann. Von diesem Zusammenhang rührt also zu Recht die Bezeichnung „Wellen"-Widerstand, weil er nur für jede einzelne dieser Teilwellen gilt; deshalb ist er auch bei Auftreten von hin- und rücklaufenden Wellen mit einer einfachen Methode schlecht zu messen.

Beim Kabel im Wellenzustand existiert nur die hinlaufende Welle. Der Wellenwiderstand ist also derjenige Widerstand eines Kabels, den man am Eingang messen könnte, wenn das Kabel unendlich lang wäre. Oder anders ausgedrückt: Will man Reflexion verhindern, dann muß man ein kurzes Kabel in ein scheinbar unendlich langes verwandeln, indem es am Ende mit Wellenwiderstand abgeschlossen wird. Der Lastabschluß mit Wellenwiderstand täuscht dem' Signal ein unendlich langes Kabel vor. Das Signal wird dann vollkommen von der Last absorbiert, so als ob es sich immer weiter fortpflanzen würde. Diesen angestrebten Fall, daß der Lastwiderstand dem Wellenwiderstand entspricht, nennt man

 

Wellenanpassung

Es gibt noch andere Arten der Anpassung, zum Beispiel die Leistungsanpassung. Im Sonderfall der Wellenanpassung liegt auch Leistungsanpassung vor. Ansonsten bezeichnet Leistungsanpassung das mögliche Optimum der Leistungsübertragung, die nur bei gleichzeitiger Wellcnanpassung 100% und in allen anderen Fällen kleiner ist. Die Wellenanpassung spielt von jeher dort eine große Rolle, wo Energie sehr teuer ist, etwa bei Sendeanlagen, die nur mit großer Leistung die gewünschte Reichweite erzielen. Jeder Funkamateur stimmt aus diesem Grund seine Antenne auf die Leitung ab, nicht nur, um selbst große Sendereichweiten zu erzielen, sondern vor allem auch, um schwache Empfangssignale nicht durch Reflexion zu verlieren. Auch Energieversorgungsunternehmen berücksichtigen bei Überlandleitungen die Anpassung.

Warum soll dies alles auch für HiFi wichtig sein? Leistung ist hier ja nicht unerschwinglich teuer! Tatsächlich ist jedoch bei Fehlanpassung leider nicht nur ein linearer Leistungsverlust zu beklagen, sondern dieser ist in der Regel auch frequenzabhängig, so wie der Wellenwiderstand und die Lastimpedanz frequenzabhängig sind, was unsere oberste Generalforderung nach formtreuer Signalübertragung im Kern betrifft.

Die Fehlanpassung bei einer bestimmten Frequenz kann man mit dem Verhältnis ausdrücken, welches die Spannung der reflektierten (rücklaufenden) Welle im Verhältnis zur Spannung der hinlaufenden Welle hat, was genauso für den Strom gilt. Dieses relative Verhältnis ist ein dimensionsloser Faktor, der sich - ähnlich wie beim Dämpfungsbelag a - zwischen 0 bei Wellenanpassung und 1 bei Totalreflexion bewegen kann und wird Rflexionsfaktor genannt.

 

Reflexionsfaktor

Dieser ist mit elementaren Überlegungen quantitativ herleitbar: An der Last Z1, dem Ort der Reflexion, addieren sich die Spannungen der Teilwellen U1 = Uhin + Urück und subtrahieren sich deren Ströme I1 = Ihin Irück. Für die Teilwellen gilt als Spannung/Strom-Verhältnis der Wellenwiderstand Zw, also Ihin = Uhin/Zw und  Irück = Urück/zw. Daraus folgt für die Last:

 

 

Der Reflexionsfaktor ist bei komplexem Wellenwiderstand und komplexer Last ebenfalls komplex. Wenn wir uns für die Beträge der Spannungen und Ströme interessieren, so wirkt auch nur der Betrag des Reflexionsfaktors. Zeichnen wir den Betrag des Reflexionsfaktors unserer Beispielkabel bei 8 Ohm reeller Last auf, so kommt das ganze Ausmaß des Dilemmas an den Tag (Bild 14). Erinnern wir uns, daß ein Reflexionsfaktor von 1 Totalreflexion bedeutet, und r = 0,5 besagt, daß an der Last nur die halbe Eingangsspannung zur Verfügung steht.

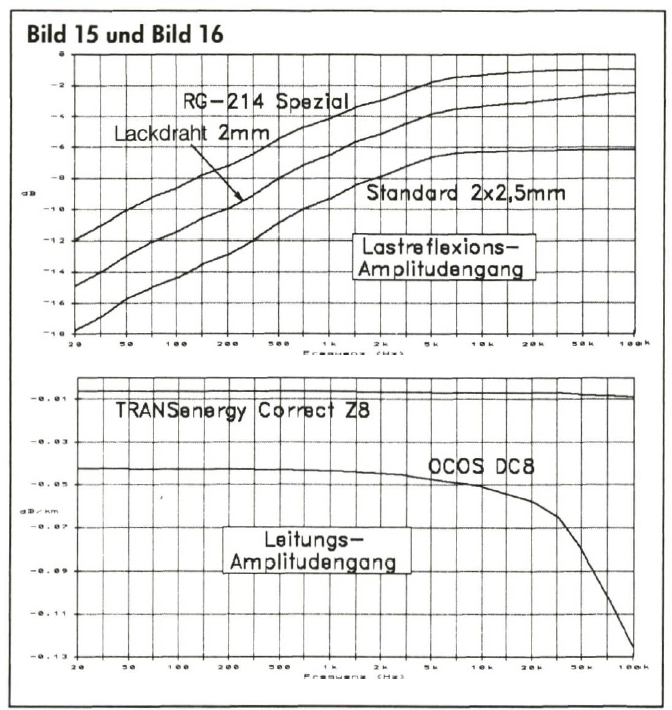
Im HiFi-Bereich sind wir gewohnt, in Amplitudenfrequenzgängen zu denken und zu vergleichen, daher wäre es interessant zu wissen, wie sich die durch Reflexion verursachte Pegelminderung in dB ausdrükken läßt. Analog der Pegelminderung durch die Kabeldämpfung, die mit 20 log (1 - a) berechnet wurde , können wir die Pegelminderung durch Reflexion mit 20 log (1 - r) angeben (Bild 15).

Beim Betrachten dieser Kurven wird das erste Erschrecken über die Größenordnung der Amplitudenbedämpfung im Tieftonbereich sicherlich dem Zweifel weichen, ob dies alles seine Richtigkeit hat. 12 dB Bedämpfung und mehr, das kann es doch niemals geben? (Was passiert, wenn ein 50-HF-Kabel als Kleinsignalkabel mit 1OOk abgeschlossen wird, bleibe vorläufig der Phantasie des Lesers überlassen.) Warum sind Klangunterschiede bei Kabeln trotzdem relativ mühevoll auszumachen und jahrzehntelang ignoriert worden?

Die Antwort hat zweierlei Aspekte. Zum einen liegt in aller Regel auch ohne Kabel Fehlanpassung vor: Die Eingangsimpedanz der Endstufe stimmt mit der Ausgangsimpedanz der Vorstufe nicht überein; der Innenwiderstand des Endstufenausgangs unterscheidet sich gravierend von der Lautsprecherimpedanz. Auf diese Weise relativiert sich die Fehlanpassung durch das Kabel. Bei reflexionsfreien Kabelverbindungen tritt dieser Pegelverlust nicht ein. Sie können daher bei gleichem Dämpfungsverhalten lauter „klingen“ als Normalkabel, und vor allem wird die ganze Tieftonleistung vonder Last absorbiert. Dieser Umstand wird ihnen dann gelegentlich bei Klangvergleichen in Umdrehung der Tatsachen als Baßbetonung angekreidet, dabei sind es die Lautsprecherboxen, die jahrzehntelang mit falschen Kabeln auf „Baßtüchtigkeit“ getrimmt wurden.

Überhaupt ist bei Kabelhörvergleichen infolge Undefinierter Anpassungsverhältnisse die Wahrscheinlichkeit überwältigend, daß nicht Kabel, sondern Äpfel mit Birnen verglichen werden. In weiterer Beantwortung unserer Frage, warum derart gravierende Pegelverluste sich nicht ebenso deutlich hörbar machen, muß gesagt werden, daß wieder einmal - wie so oft - der Teufel mit Beelzebub ausgetrieben, aus der Not eine Tugend gemacht wird: Die infolge Reflexion zurücklaufende Welle trifft am Kabeleingang ebenfalls auf eine Fehlanpassung, bei der ein anderer Reflexionsfaktor gilt. Nach nochmaliger Teilreflexion erscheint sie geschwächt ein zweites Mal am Ausgang und wird erneut teilweise absorbiert, teilweise reflektiert. Dieses Spiel wiederholt sich, bis die Energie durch Leitungsdämpfung und Absorption aufgebraucht ist.

Damit wird die durch alleinige Lastreflexion verursachte gewichtige Dämpfung energetisch gemindert, doch bedeutet dies, daß jedem Impuls ein Schwanz an Mehrfachreflexionen folgt. Würde also am Kabeleingang Anpassung vorliegen, so würde die in Bild 15 gezeigte Dämpfung voll wirksam werden. Die eingangsseitige Anpassung würde bei Fehlanpassung am Ausgang zumindest Mehrfachreflexionen verhindern. Bei rcflcxions- freier Anpassung am Ausgang ist die Eingangsanpassung vom Kabelstandpunkt aus allerdings nicht mehr notwendig.

Kommen wir hier noch einmal zurück zu unseren Beispielen mit Fernsehantennenkabeln. Dort ist man sich der Problematik durchaus bewußt. Werden Fehler gemacht durch Einsatz falscher oder minderwertiger Kabel mit abweichendem Wellenwiderstand oder durch Mehrfachanschlüsse parallel an einer Zuleitung ohne entsprechende Anpassungsglieder, so treten am Fernsehschirm störende Geisterbilder auf, verursacht durch Mehrfachreflexionen an den Fehlanpassungsstellen. Und eben dasselbe spielt sich bei Verbindungen unserer Hi-Fi-Geräte ab. Was wir hören sind nicht gestochen scharfe Klangbilder, sondern verzerrte und verschwommene Klangeindrücke und Geisterbilder!

 

 

Was verspricht Abhilfe? Nicht das Versilbern der Leitungen, auch nicht Drähte aus 24-Karat-Massiv-Gold und erst recht nicht das Versprechen der Werbung, daß die NASA-Astronauten dieses Material zum Schnüren ihrer Stiefel verwenden, sondern einzig und allein muß als Konsequenz die Anpassung der Last an den Wellenwiderstand des Kabels oder umgekehrt des Wellenwiderstandes an die Last gefordert werden. Wie steht es in diesem Zusammenhang mit den modischen Stegleitungen bei Lautsprecherkabeln? Hat ihre Existenz noch einen anderen tieferen Hintergrund, außer daß sich der Steg hervorragend für Werbezwecke bedrucken läßt und man an der Farbgebung endlich die unterschiedlichen Preisklassen erkennen kann, wenn man sie schon nicht hört? Stegleitungen sind so wenig verzerrungsfrei wie andere auch. Ihr Wcllenwiderstand jedoch wird nicht wie angestrebt niederohmig, sondern steigt bis aufs Doppelte von Normalkabeln, also bis über 200 (siehe auch Proximity-Effekt). Daß sie entsprechend anders klingen, liegt auf der Hand, und nur darauf scheint es wohl anzukommen. Es ist schon erstaunlich, was dem HiFi-Liebhaber an atemberaubendem Fortschritt zugemutet und von diesem auch akzeptiert wird!

Die Frequenzabhängigkeit des Wellenwiderstandes von Normalkabeln vor Augen, scheint es unmöglich zu sein, eine Anpassung herbeizuführen. Ein Grund mehr, bei Kabeln die Verzerrungsfreiheit anzustreben, denn die Erfüllung der Heaviside-Relation beinhaltet, daß der Wellenwiderstand im ganzen Übertragungsbereich reell und linear ist. Umgekehrt bedeutet ein vom Wellenwiderstand abweichender Abschluß einer ansonsten verzerrungsfreien Leitung aber auch, daß diese nicht voll wirksam werden kann. Bei einer Überanpassung (Lastwiderstand größer als Wellenwiderstand) tritt zunehmend die Leitungskapazität in Erscheinung; bei Unteranpassung (Lastwiderstand kleiner als Wellenwiderstand) wirkt zunehmend die Leitungsinduktivität. Solche kapazitiven und induktiven Anpassungsfehler tragen übrigens stark zu einer Verformung und Verlängerung von Rechteckimpulsen (Digitaltechnik) bei. Die Verzerrungsfreiheit eines Kabels würde also durch Fehlanpassung wieder zunichte gemacht. Folglich müssen wir in unsere „Kabelrezeptur" den Abschluß mit Wellenwiderstand einbinden. Setzen wir die Formel für den Wellenwiderstand in die Heaviside-Relation ein, so ergibt sich die Beziehung:

 

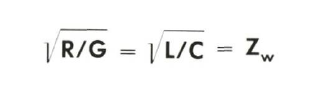
Wir wollen sie als erweiterte Heaviside-Relation bezeichnen. Nur Kabel, die dieser Beziehung im ganzen Audio-Frequenzbereich genügen, sind wirkliche NF-Kabel. Alles andere ist schlichtweg Etikettenschwindel!

 

Realisierung von verzerrungsfreien Kabeln

Das Vorgehen zur Verwirklichung von NF-Kabeln ist durch unsere „Rezeptur“ vorgezeichnet. Zunächst entscheidet man sich, für welchen Lastabschluß das Kabel eingesetzt werden soll: beim Lautsprecherkabel zum Beispiel nominal 4 oder 8 Ohm. Dies ist leider wiederum ein Kompromiß, denn nur wenige Lautsprecherboxen haben eine lineare und reelle Impedanz von 8. Und wenn schon, dann meistens auch niedriger: Nach DIN kann das Impedanzminimum für 8-Boxen bis 6,4 sinken, was von den Chassisherstellern gern ausgenutzt wird, weil es höheren Wirkungsgrad bedeutet.

Liegt der Lastabschluß fest, so grenzt die erweiterte Heaviside- Relation den Spielraum für die Leitungsparameter ein. Über die Leitungsgeometrie sind die Induktivität und die Kapazität, wie wir wissen, gewissermaßen aneinander gekoppelt. Der Widerstand resultiert ebenfalls aus der Leitungsgeometrie und hat Einfluß auf die Induktivität. Die Ableitung schließlich hängt vom Dielektrikum und der Geometrie und damit wiederum von der Kapazität ab. Mit anderen Worten: Bei jedem Entwicklungsschritt zur homogenen, verzerrungsfreien Kabellösung müssen jedes Mal sämtliche Leitungsparameter gleichzeitig geändert werden.

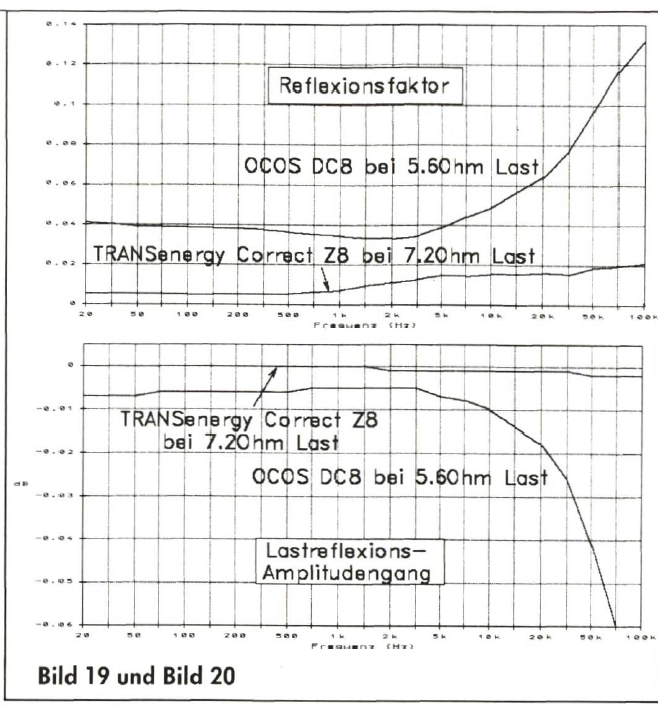
Eine langwierige, mühevolle und trickreiche Gratwanderung kann letztlich zum Ziel führen. „Kann“ deshalb, weil nicht alle eventuell gewünschten Wellenwiderstände ohne weiteres zu realisieren sind, hohe Werte für den Wellenwiderstand schon gleich gar nicht. Das einzige bekannte Beispiel für ein solchermaßen entstandenes NF-Kabel ist das OCOS-DC8 siehe Bild 16 bis 20. Beim OCOS-DC8 wurde der Trick angewandt, die Ableitung durch „Verunreinigung“ des Dielektrikums auf das erforderliche Maß zu erhöhen. Eine andere Möglichkeit besteht darin, durch künstlichen Eingriff Abweichungen einzelner Parameter vom theoretisch geforderten Wert zu beheben.

 

 

Korrigierte Kabel

Sie werden durch Einbau konzentrierter Bauelemente in regelmäßigen Abständen in das Kabel verwirklicht, so daß für die Leitung als Ganzes die Heaviside-Relation erfüllt wird. Dieses Vorgehen ist leider nicht bei jedem Kabel möglich und setzt wegen der Frequenzunabhängigkeit der diskreten Bauelemente bereits frequenzunabhängige Leitungsparameter voraus. Dennoch ist diese Methode flexibler und gezielter einsetzbar, durch den hohen manuellen Arbeitsaufwand leider jedoch auch relativ kostspielig. Der Urvater eines korrigierten Kabels ist die pupinisierte Fernmeldeleitung; ein aktuelles Beispiel ist das TRANSenergy Correct Z8 Lautsprecherkabel (Bild 16 bis 20).

Es ist klar, daß punktuell korrigierte Kabel im Inneren nicht mehr als homogen anzusehen sind. Tatsächlich bestehen sie aus einer Aneinanderreihung von homogenen Teilstücken mit dazwischen befindlicher Stör- oder Stoßstelle von ganz bestimmter Beschaffenheit, und zwar derart, daß die Stoßstelle das zugehörige Leitungsstück mit komplexem Verhalten zu einem reellen kompensiert. Es liegt also konjugiert komplexer Abschluß der Teilstücke vor, was mit Leistungsanpassung gleichzusetzen ist. Nach außen verhält sich das Kabel reell, also verzerrungsfrei. Verzerrungs- und reflexionsfreie echte NF-Kabel für den engagierten HiFi-Liebhaber: Das ist die Antwort, die die Leitungstheorie dem Kabellatein der HiFi-Münch- hausens entgegensetzen kann. Dies heißt nicht, daß es nicht über die Leitungstheorie hinausgehende Ansatzpunkte für weitere Erforschung von heute noch ungeklärten Phänomenen geben kann. Doch wer sich damit zu befassen wagt, sollte die Möglichkeiten auf der Grundlage der Leitungstheorie erst überzeugend ausschöpfen, will er noch ernstgenommen werden und sich nicht der Scharlatanerie verdächtigen lassen.