Digital Sound

Allzusehr hat die Gewöhnung dazu geführt, unter „Digital“ automatisch Compact-Disc-Qualität zu verstehen. Aber Digital und Digital kann etwas mehr oder minder Anderes sein. So zeigten 1982 noch einige PCM-Pseudovideo-Adapter Schwächen, weshalb sie gar nicht so überragend gegenüber einem Zweispur- 19-cm/s-Spulengerät mit Dolby B abschnitten. Auch in der Studiotechnik kreucht noch so einiges an Digital-Equipment aus frühen Jahren herum, bei Kenntnis der CD-Qualität kann da nur die Nase gerümpft werden. Damals war die Zeit eben noch nicht wirklich reif und die digitalen Bausteine für Tonaufnahme noch recht schlecht und/oder viel zu teuer. Der 8mm-Videorecorder zeigt, daß bei Digital und auch beim Schrägspur-FM-Ton deutliche Unterschiede zum bisher Gewohnten auftreten.

 

Bias + FM + PCM

„FM“ gilt fast als das Synonym für UKW-Rundfunk. Daß auch die krächzenden Civilband-Sprechfunkgeräte (CB) mit Frequenzmodulation arbeiten, wird leicht verdrängt. Sie arbeiten für die Sprachübermittlung mit einer eingegrenzten Frequenzbandbreite und einem geringen Frequenzhub. Der wiederum bedeutet eine geringere Aussteuerung des Demodulators im Empfänger und damit deutliches Rauschen.

Eine konventionelle Tonaufzeichnung über Längsspur mit Vormagnetisierung am Bandrand ist zwar bei manchen 8mm-Recordern auch möglich, insgesamt aber eher ein Notbehelf. Alle 8mm-Recorder verfügen über FM- Ton als Normalausstattung. Gegenüber dem bisher gewohnten Ton (oder wie soll man das dumpfe Gemauschel nennen) bei Halbzoll-Recordern ist der 8mm-FM-Ton trotz Mono ein Fortschritt. Er bietet geringeres Rauschen und eine saubere Hochtonwiedergabe, klanglich liegt er jedoch merkbar unter dem Niveau von HiFi-FM-Videorecordern.

 

Für Bild schmal, für Ton breit

Das 8-mm-Band nimmt eine Position ein zwischen dem bekannten Halbzoll- (12,7 mm) Videoband und dem zirka 1/4 Zoll breiten Spulenband (6,3 mm). Zwei Cassetten-Schnürsenkel (3,8 mm) nebeneinandergeklebt ergeben ganz knapp das neue Band. Vom System her erlaubt das 8mm-PCM-System die gleichzeitige  Aufnahme von zwölf Monoprogrammen oder zwölf-kanaligem Surround-Sound oder drei Quadroprogrammen. Die sechs PCM-Teilspuren können natürlich auch gleichzeitig heruntergelesen werden. Allerdings muß dann das System gegen den Spurversatz zwischen den Segmenten kämpfen (siehe auch Spurbild), zumindest wenn der Videokopf die Signale nicht gleichzeitig in einer Linie aufgezeichnet hat.

Die sechs Spuren werden durch eine Zeitverzögerung (jeweils gut 3 Millisekunden) getrennt. Der Videokopf läuft in die Spur ein, die Verzögerung schaltet seine Aufnahme- oder Wiedergabefunktion aber erst entsprechend der Spuranwahl ein, und dann auch nur für eine Zeit von wiederum gut drei ms. Am Anfang eines jeden geschriebenen Segments stehen Synchronimpulse; damit wird der Datenseparator auf Vordermann gebracht und liegt dann richtig im „eyepattern“. Am Ende bleibt ein kurzes Stück unbeschrieben als Sicherheit, um nicht das folgende Segment zu überschreiben.

Dieses spezielle PCM-System ist übrigens in Deutschland nicht ganz neu. Bereits das HiFi-Tonsystem von Grundigs Video 2000 verfügte über eine dem 8mm-Ton entsprechende Aufzeichnung. Die V2000-Wendekassette konnte so 6 x 4 x 2 Stunden = 48 Stunden Musik speichern. Im Longplaymodus reichen dann zwei Cassetten für mehr als eine Woche Musik. Eine spezielle Spur gestattet, auf dem 8mm-Band einen Code für Suchvorgänge aufzusprechen. Spätere Geräte werden hiermit nicht nur die Stückanfänge leicht finden können.

 

 

Quantisierungsstörgeräusche im Zickzack

 

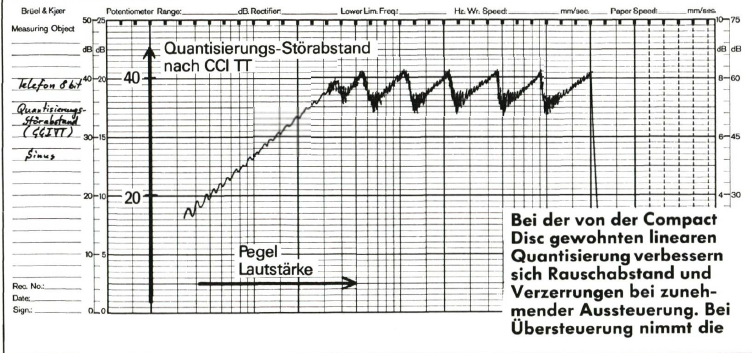
Qualität dann allerdings recht plötzlich wieder ab. Bei Systemen mit Kompandern erhöht sich der Störabstand ab einem bestimmten Aussteuerungsniveau nur noch im Zickzack. Bei Erreichen einer Aussteuerungsschwelle vergrößert die Kompressorfunktion die Quantisierungsstufe (hier Verdoppelung für alle 6 Dezibel Aussteuerungserhöhung), der Quantisierungsfehler und damit die Störungen steigen dabei wieder an.

 

Berauschende Modulation

So wie die Unbill der deutschen Sprache immer wieder die Fotografen mit Tiefenschärfe und Schärfentiefe plagt, so treibt Rauschmodulation und Modulationsrauschen HiFi-Köpfe zum Rauchen. Wird das im Hintergrund noch durchhörbare, nirgendwo vermeidbare, Rauschen in Abhängigkeit vom Nutzsignal (Musik) lauter und leiser, so wird es moduliert. Diese Rauschmodulation kann bereits ein sehr leises Rauschen auffällig machen. Ein lautes gleichmäßiges Fauchen oder Hissen stört oft weniger. Die Veränderung (Modulation) ist der eigentlich störende Effekt. Das Modulationsrauschen dagegen weist darauf hin, daß erst das Nutzsignal selbst ein Rauschen erzeugt. So ist gerade beim Analogband jeder Ton von einem leichten Rauschschleier umgeben. Die ungleichförmig ausgebildeten und verteilten Magnetteilchen in der Bandschicht bedingen es. Aber auch der Rauschanteil, der, sobald ein lauter Nutzton erklingt, durch ein Rauschverminderungssystem (Kompander) weniger stark unterdrückt wird, kann als Modulationsrauschen gelten. Es sind eben eineiige Zwillingsbegriffe.

Das Modulationsrauschen einer analogen Bandspeicherung verschwindet sofort nach dem Ton wieder. Ein (analoges) Kompandersystem stellt erst langsam die volle Rauschverminderung wieder her, die Rauschschleppe (oder -fahne) kann dann hörbar werden. Breitband-Rauschverminderer (dbx und High Com) müssen langsamer nachstellen, da sie sonst starke Verzerrungen im Baßbereich produzieren. High Com allerdings wendet einen Trick an (automatisch umschaltende Zeitkonstante), so daß es fast so frei von Rauschfahnen wie die Dolby-Systeme dasteht. Digitale Kompander können im Gegensatz zu analogen ohne jede Verzögerung reagieren. Bei blockweiser Kompandierung treten allerdings auch hier Reaktionszeiten von knapp 1 bis zu 20 Millisekunden auf. Hierbei kann das digitale System auch einmal schon vor Auftreten des eigentlichen Tons ansprechen, da dieser durch Zwischenspeicher verzögert wurde. Das Kausalitätsprinzip gilt auch hier nicht als aufgehoben. Digitale Systeme können allerdings recht leicht das Erscheinen der Ursache verzögern (das gilt auch für die Vorschwinger der Oversampling-CD-Spieler), die Wirkung scheint dann vor der Ursache zu kommen. Das Diagramm für lineare Quantisierung zeigt als Rauschniveau den praxisähnlichen Störpegel (siehe in stereoplay die Messung der „Nutzsignaldynamik“ mit der DHFI-Testplatte). Das Rauschniveau für Digital-Null (totgeschaltet) liegt tiefer, wird aber in der Praxis nie in einem Musikstück erreicht.

 

 

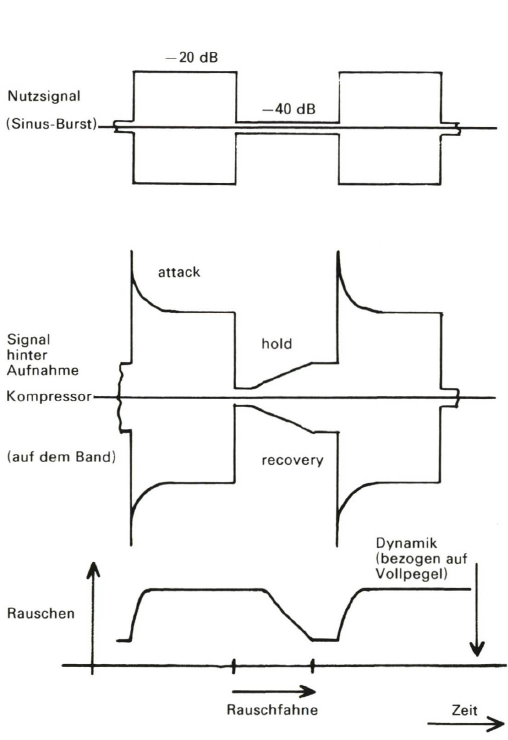
Ein analoger Kompander erzeugt bei Pegelerhöhung eine hohe Pegelspitze (die verarbeitet das Band meist nur mit Verzerrungen). Nach dieser Ansprechzeit (attacktime) schwingt der Kompressor auf den endgültigen Pegel ein.

Bei Pegelabsenkung vermindert der Kompressor erst das Signal zu stark und geht dann langsam nach einer Haltezeit (’hold time’) und einer Erholungszeit (’recovery time’) auf den endgültigen Pegel über. Die Rauschverminderung ist erst wieder nach Ablauf von hold und recovery time voll wirksam. Insbesondere bei Kopfhörer-Wiedergabe [geringerer Raumnachhall) kann diese verspätete Rauschverminderung störend als Rauschfahne erkannt werden.

 

Wat is denn dat DAT da?

Digital Audio Tape wird noch Jahre bis zur Markteinführung in Deutschland benötigen. Es wird eine Lösung mit Schrägspuraufzeichnung werden (R-DAT, rotierender Kopf). Die notwendigen technischen Verfahren sind gebräuchlich. Die Konkurrenz mit Längsaufzeichnung benötigt dagegen noch Jahre, um Tonköpfe für die vielen parallelen, superschmalen Spuren im noch verkaufbaren Kostenrahmen zu fertigen (S-DAT, stehender Kopf). Jede der 8 bis 16 Aufzeichnungsspuren benötigt eine eigene Verstärkerelektronik. Der Azimut muß exakt stimmen, sonst laufen die Datenkanäle zeitlich auseinander. Auch befriedigt die maximale Aufzeichnungszeit bei der Längsspuraufzeichnung nicht. Während sie nur ähnliche Zeiten wie die Compact- Cassette bietet, schafft die Schrägspuraufzeichnung zwei (später auch drei) Stunden, und das alles mit einer Cassette von der Grundfläche einer Scheckkarte.

Das Argument der fertig produzierten Software kann keines der beiden Systeme für sich entscheiden. Hochgeschwindigkeitsduplizieranlagen für die vielen Parallelspuren von S-DAT zeigen Probleme in der exakten Höhenführung (Spurversatz) und bei den geforderten besonders kleinen Wellenlängen auch im Band-Kopf-Kontakt. Die Kopfmaterialien plagen sich zudem mit den besonders hohen Frequenzen, da gleichzeitig große Aufzeichnungsfeldstärken gefordert werden (auch hier hochkoerzitive Beschichtung). Bänder mit Schrägspuraufzeichnung können durchaus auch schnell dupliziert werden, und zwar als Kontaktkopie. Speziallaufwerke erstellen spiegelbildliche Masterbänder. Diese laufen zusammen mit einem jungfräulichen Band, die Butterseiten aufeinander, unter Druckkontakt durch eine HF-Spule. Unter Einfluß des Vormagnetisierungsfelds prägt sich die Aufzeichnung des Masterbandes auf das frische Band. Im Gegensatz zum ungewollten Kopiereffekt (Vor- und Nachecho) ist diese Aufzeichnung stark und stabil. Bei R-DAT allerdings versagt sie. Das Masterband muß in der Koerzitivkraft wesentlich höher liegen als die Kopie. In der Kombination Metal-Tape als Master und Chrom oder Chrom-Substitut als Kopie gilt das nicht als Problem, aber was, wenn die Kopie bereits ein Metal-Tape sein muß?

 

5 Stereo = 1 Bild

 

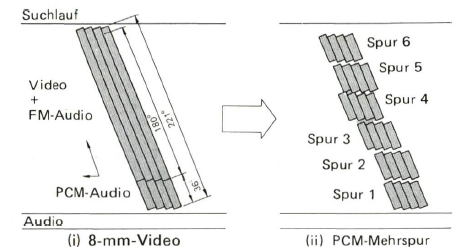
Auf 180 Grad Kopftrommeldrehung passen ein Bild oder fünf PCM-Stereoprogramme. Zusätzliche 36 Grad Umschlingung bietet ein auch mit dem Bild zusammen nutzbares und sogar noch nachträglich vertonbares HiFi-Stereo-Ton-programm.

 

8mm mit Super-Preemphasis

 

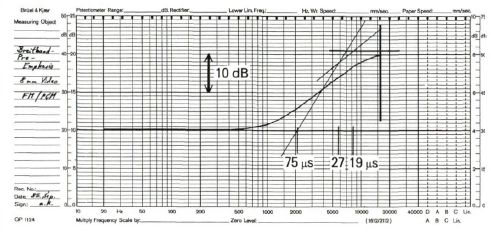
FM-Ton wie auch der PCM-Ton arbeiten bei 8mm mit demselben Kompandersystem. Die Höhenanhebung für breitbandige Signale ist ungewöhnlich hoch, die Progression wird zu den höchsten Höhen aber wieder zurückgenommen (75 und 27 sowie 75 und 19 Mikrosekunden)

 

Heiße Bänder mit Curie 

Ein anderes Kontaktkopierverfahren arbeitet mit Hitze, funktioniert allerdings nur mit echtem Chromdioxid. Dessen magnetische Eigenschaften brechen schon bereits unterhalb 200 Grad Celsius zusammen (Curietemperatur). Ein Laserstrahl erwärmt das Kopieband zeilenweise kurzzeitig über die Curietemperatur. Beim Erkalten „friert“ das vom Masterband erzeugte magnetische Feld auch auf der Kopie ein.

Hier tritt das Problem auf, daß ein Super-Chromdioxid fehlt, das ähnlich hoch koerzitiv wäre wie Metallpigment. Heute verfügbares Cr02 reicht für 8mm-Video und erst recht für PCM auf R-DAT in der Koerzitivkraft nicht aus. R-DAT mit Schrägspuraufzeichnung kann in den Daten vergleichbar mit der CD arbeiten (16 Bit linear) oder auch mit heutigem PCM als Pseudovideo (14 Bit mit Preemphasis). Qualitativ wäre es damit dem 8mm-PCM-Ton überlegen. Lösungen sind denkbar mit umschaltbarer Sampling-Frequenz, und zwar für 32 KiloHertz zur Direktaufzeichnung von Satellitenrundfunk ohne Analogwandlung, bei 44,1 kHz dasselbe für die CD und bei 48 kHz mit etwas mehr Sicherheit gegen Aliasingstörungen für hochwertige Eigenaufnahmen.

 

10 bit auf 8 bit

 

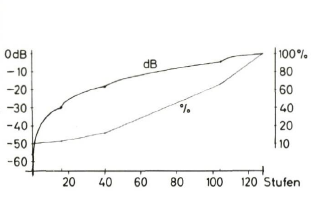
ln den zweimal 128 Stufen von 8 bit werden 2 x 512 Stufen eines 10-bit-Wandlers untergebracht. Die Kompressionskurven verlaufen linear (Prozent) und logarithmisch.

 

Nichtlineare Quantisierung

 

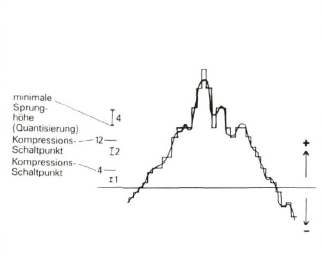
Bei großen Amplituden können nur größere Spannungssprünge dargestellt werden, Feinheiten verschluckt ein solches System. Zum Glück kann auch das Ohr solche Feinheiten nur noch undeutlich heraushören.

 

1-Bit-Supersampling

Vor lauter PCM wird die Delta-Modulation (DM) ganz vergessen, dbx stellte einmal einen DM-Prozessor zum Anschluß an einen Videorecorder vor. Dieser brachte es auf über 120 Dezibel Pausendynamik. Allerdings ließ er die Klirrarmut von 14- oder 16-bit-PCM vermissen und zeigte leichte, aber eben doch noch hörbare Rauschmodulationen und Hochtonverzerrungen. Die Dolby-Laboratorien dagegen überraschten mit einem Konzept für eine besonders preisgünstige Digitalübertragung. Sie kamen ohne üblichen D/A-Wandler-Baustein aus und mußten nicht mit präzise tolerierten Bauteilen arbeiten. Beide Systeme arbeiteten mit Kompandern, die analog arbeiten, allerdings von dem digitalen Signal sehr exakt gesteuert wurden.

DM sampelt mit 250 bis über 800 KHz. Das eine Bit schaltet aber lediglich zwischen Plus und Minus um. Solange das Bit gesetzt ist, wird die Ausgangsspannung laufend größer (positiver), ist es nicht gesetzt, so wird die Spannung negativ. Bei hohen Aussteuerungen und hohen Frequenzen hat ein DM- System aber Probleme, es kommt nicht nach, die Anstiegsgeschwindigkeit (slew-rate) reicht nicht, dbx und Dolby haben hier mit einem Kompander und einer Fehlerrückführung nachgeholfen. Eine wesentliche Verbesserung ist die automatische Anpassung an laute hochfrequente Töne, dabei wird umgeschaltet auf eine sich beschleunigt ändernde Ausgangsspannung, so daß die Anstiegsgeschwindigkeit ausreicht.

Gegenüber Übertragungsfehlern verhält sich DM sehr robust. Da immer nur die Änderung gegenüber dem bisherigen Wert bei DM übertragen wird, kann ein Ausfall der Daten nur bewirken, daß der alte Wert beibehalten wird. Bei PCM kann dagegen ein völlig anderer Spannungswert durch einen einzigen Bitfehler entstehen, so kann der Wert von Plus auf voll Minus springen, was laut kracht. Während bei PCM Übertragungsfehler in jedem Fall durch Rechenschaltungen korrigiert werden müssen, reichen bei DM recht einfache Fehlererkennungsstrategien, eventuell kommt ein einfaches System auch ganz ohne aus.

Die Dolby-Laboratorien haben dabei die Unzulänglichkeiten des Gehörs ausgenutzt. Ein Nutzton kann ein Störsignal zeitlich verdek- ken, also während er erklingt. Aber auch kurz davor und etwas länger danach ist das Störsignal kaum wahrnehmbar, obwohl in voller Stärke vorhanden. Genauso kann eine Verdeckung auch im Frequenzbereich unterhalb (geringfügig) und oberhalb des Nutztones (deutliche Wirkung) erfolgen. Das Störgerümpel ist durchaus da, aber es wird durch den Kompander, ähnlich wie auch vom Dolby B und C bekannt, geschickt das Sofa davorgestellt.

Während bei PCM über Pseudovideo eine Datenrate von ungefähr 2 Millionen Bit je Sekunde (Mbit/s) übertragen werden muß (inklusive den Datenwörtern zur Fehlerkorrektur), kommt 8-mm-PCM je Stereoton mit nur 500 Kbit/s (ohne Fehlerkorrekturworte) und gut 600 Kbit/s inklusive Fehlerkorrektur aus. Das kostengünstige digitale Dolby-System benötigt dagegen nur 250 Kilobit je Sekunde, die Fehlerkorrektur beansprucht dabei fast keinen Platz. Die Bitrate ist ein Kostenfaktor bei der Speicherung und bei der Fernübermittlung. 

 

Digitaler Hörfunk über Satellit

Durch die wachsende Verbreitung von digitalen Verfahren für Aufnahme und Wiedergabe wie etwa in Mischpulten und CD-Playern ist es notwendig geworden, die Rundfunkübertragungen auf dasselbe hohe Qualitätsniveau zu heben. Ein analoges Tonsignal wird zur Digitalisierung mit einer Frequenz abgetastet, die mindestens doppelt so hoch ist wie die obere Grenzfrequenz des zu übertragenden Tonsignals (Abtasttheorem). Es werden aus dem zeitkontinuierlichen Tonsignal also zeitdiskrete Werte abgeleitet. Zeitdiskret bedeutet im Gegensatz zu zeitkontinuierlich, daß die „Zeitachse“ des Tonsignals in einzelne kurze Zeitbereiche unterteilt wird. Die Dauer eines solchen Zeitbereichs ist gleich dem Kehrwert der Abtastfrequenz. Ein Abtast/-Halte-Glied (Sample/Hold) setzt den Abtastwert jedes Zeitbereichs dem zeitlichen Mittelwert der Amplitude des analogen Signals im jeweiligen Zeitbereich gleich.

Diese zeitdiskreten Abtastwerte besitzen eine kontinuierliche Amplitude (Wert). Da sie in Form von Dualzahlen (siehe Technikbeilage XX, August ’85) gesendet werden sollen, kann nicht jede beliebige Amplitude übertragen werden. Mit einer 16-Bit-Codierung kann man zum Beispiel „nur“ 216 = 65 536 unterschiedliche Amplitudenwerte übertragen. Aus diesem Grund teilt ein Quantisierer den gesamten Wertebereich (der Abstand vom Übersteuerungspegel zum Rauschpegel) wiederum in diskrete Teilbereiche ein und ordnet jeden Abtastwert entsprechend seiner Amplitude in einen der vielen Teilbereiche ein. Ein Codierer weist jedem Teilbereich ein entsprechendes 16-Bit-Codewort zu. Das abgetastete Signal ist nun sowohl wertdiskret als auch zeitdiskret. Die Qualität dieses Puls-Code-modulierten (PCM-) Signalsist also durch die beiden Parameter Abtastfrequenz fa und Auflösung (Quantisierung), das heißt die Zahl der Bits pro Abtastwert bestimmt.

Hieraus läßt sich die Zahl der Bits errechnen, die pro Sekunde durch einen digitalen Rundfunkübertragungskanal geschleust werden müssen. Sie ist gleich dem Produkt aus Abtastfrequenz und Auflösung zuzüglich einiger Bits zur Fehlererkennung und zur Übertragung von Zusatzinformationen, den Rahmeninformationen. Die digitale Rundfunkübertragungskette besteht aus Studio, Zuführungskabel zur Erdstation, Sender, Satellit und Empfangsstation, (Kabelverteilstrecke und) Satellitenempfänger mit Digital/Analog-Wandler.

 

 

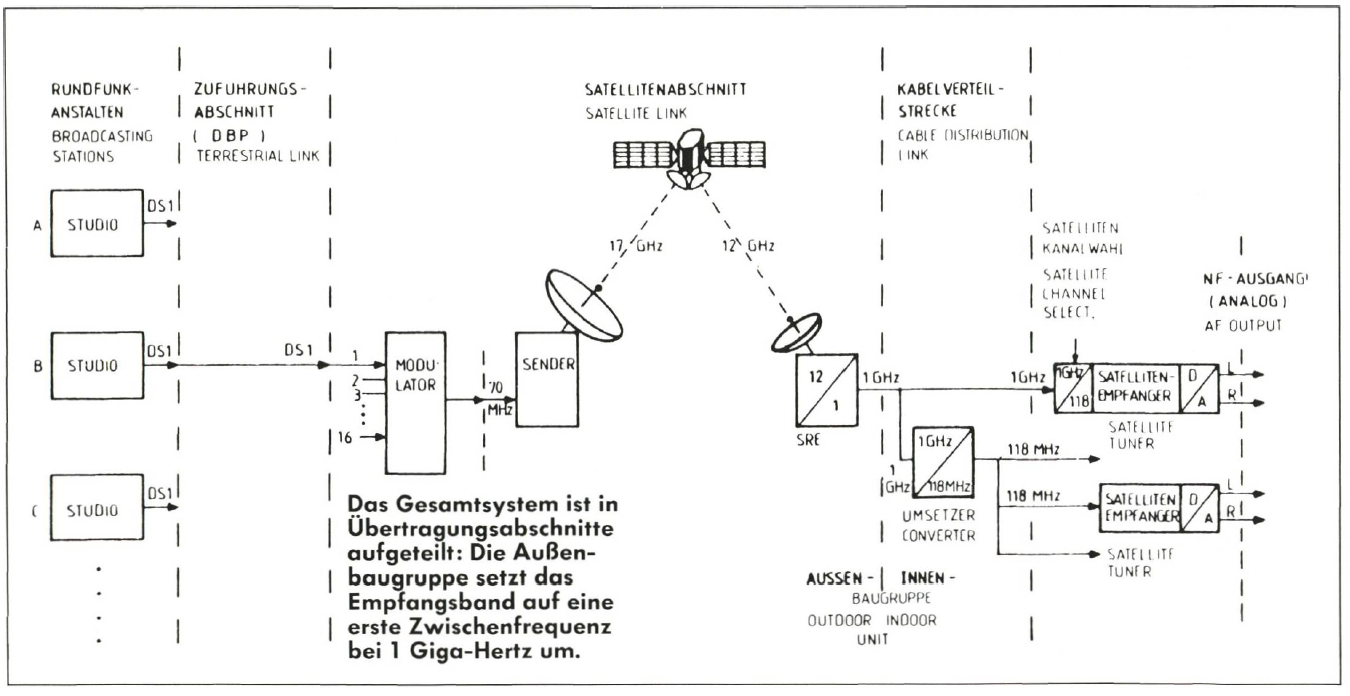
Zur Satellitenübertragung werden mehrere Einzelkanäle im Zeitmultiplexverfahren zu einem Transponderkanal zusammengefaßt. Die festgelegte Frequenzbandbreite eines Einzelkanals begrenzt die maximal darin übertragbare Anzahl von Bits je Sekunde, also die Frequenzbandbreite und die Dynamik des zu übertragenden Audiosignals.

Als zu übertragende Frequenzbandbreite einigten die Entwicklungskommissionen sich auf 15 Kilohertz. Die Systemdynamik bestimmt sich näherungsweise aus 6 Dezibel (dB) je Quantisierungsbit (1 Bit bedeutet eine Verdopplung der Dynamik) + 2 dB - 14 dB Korrekturfaktor. Der Korrekturfaktor von 14 dB rührt von einer Umrechnung des Störgeräuschpegels auf CCIR. Meßmethodenempfehlung (zirka 12 dB) und von Eigenfehlern in der Analog/Digital-Wandlerrechnung (zirka 2 dB) her. Bei der Bestimmung der tatsächlichen Nutzdynamik ist noch ein Übersteuerungs-Sicherheitsabstand (head-room) von zirka 10 dB und ein Rauschsicherheitsabstand (footroom) von zirka 10 dB zu berücksichtigen. Bei einem CD-Spieler mit 16 Bit Quantisierung ergibt sich also eine nutzbare Dynamik von 16 x 6 dB = 96dB plus 2 dB - 14 dB Korrekturfaktor - headroom - footroom = 64 dB.

Diese 16 Bit sind auf den Zuführungsstrecken der Post von den Rundfunksanstalten zur Satellitensendestation leider nicht frequenzbandbreitenökonomisch übertragbar. Bei der Zuführungstechnik kommen symmetrische und Koaxialkabel sowie Satelliten- und Glasfaserverbindungen in Betracht. Die Post unterteilt die Frequenzbandbreite dieser Übertragungsmedien ihres im Aufbau befindlichen Digitalnetzes unter Zugrundelegung einer bandbreitenökonomischen Fernsprechübertragung in Kanalbündel mit einer Bruttobitrate (samt Rahmeninformationen) von 2048 Kilobit pro Sekunde, was eine Nettobitrate (ohne Rahmeninformationen) von 1920 kBit/s liefert.

Bei Rundfunkübertragung mit einer Wortlänge von 16 Bit + 1 Bit zur Fehlererkennung und einer Abtastfrequenz von 32 kHz benötigt ein Tonkanal eine Bitrate von 17x32 000 Bit/s = 544 kBit/s. Man könnte maximal drei Tonkanäle in einem Kanalbündel mit 1920 kBit/s Nettobitrate unterbringen, wobei allerdings 1920 kBit - 3x544 kBit/s = 288 kBit/s ungenutzt blieben. Eine bessere Ausnutzung eines Kanalbündels ermöglicht die gewählte Wortlänge von 14 Bit. Flierbei besitzt ein einzelner Kanal eine Bitrate von 480 kBit/s, und 4 Kanäle zusammen nutzen genau die 1920 kBit/s eines Kanalbündels aus.

 

Das Abtasttheorem

Die physikalisch-mathematische Grundlage für sämtliche digitalen Speicher- und Übertragungsmethoden von an sich analogen, zeitkontinuierlichen Tonsignalen bildet das Abtasttheorem nach Shannon. Seine grundsätzliche Aussage besteht darin, daß es zur Übertragung oder Speicherung eines bandbegrenzten zeitkontinuierlichen Signals genügt, daß der Sender das analoge Originalsignal mit der doppelten Grenzfrequenz abtastet und diese zeitdiskreten Abtastwerte dem Empfänger überträgt. Er kann daraus das analoge bandbegrenzte Originalsignal wieder vollständig rekonstruieren. Wäre diese Beziehung nicht erfüllt, dann müßte der Sender in jedem Zeitpunkt, also in unendlich vielen Zeitpunkten, dem Originalsignal einen Abtastwert entnehmen, in eine Dualzahl codieren und übertragen. Das wäre natürlich unmöglich.

Das abgetastete Signal stellt mathematisch eine Folge von Impulsen dar, von den Technikern als Dirac-Impuls bezeichnet. Ein Dirac-Impuls ist ein abstraktes mathematisches Gebilde. Er besitzt eine unendliche Höhe, aber eine verschwindend kurze zeitliche Dauer. Seine Fläche strebt einem endlichen Grenzwert zu und nennt sich Impulsstärke. Das abgetastete Signal läßt sich also aus der Multiplikation des Originalsignals mit einer Dirac-Impulsfolge der Impulsstärke 1 errechnen. Diese Multiplikation weist jedem einzelnen Dirac-Impuls der Dirac- Impulsfolge den Amplitudenwert des Analogsignals zum Zeitpunkt des Dirac-Impulses, das bedeutet zum Abtastzeitpunkt, als Impulsstärke zu (Ausblendeigenschaft des Dirac-Impulses aufgrund seiner verschwindenden zeitlichen Dauer).

Wichtig ist nun zu wissen, welche Information mit dieser Dirac-Impulsfolge übermittelt wird. Aufschlüsse über die Frequenzspektrumsverteilung des abgetasteten Signals, also über die Information, die das abgetastete Signal beinhaltet, liefert die Fourier-Transformation. Sie zerlegt das abgetastete Signal in eine Folge von einfachen Sinus- und Cosinus-Teilsignalen mit unterschiedlichen Frequenzen und Amplituden (Koeffizenten) der einzelnen Teilsignale sowie in einen Gleichanteil. Aus den Koeffizenten läßt sich die spektrale Verteilung des abgetasteten Signals ersehen. 

 

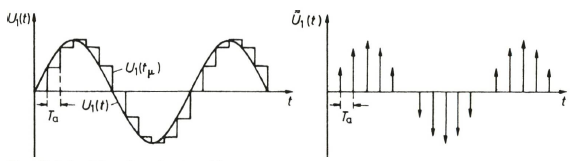
Das Originalsignal und seine Abtastwerte: Die Darstellung des abgetasteten Signals als Impulsfolge ist mathematisch „einfacher" zu behandeln.

 

Zur Untersuchung des Frequenzspektrums des abgetasteten Signals ist es zweckmäßig, die Darstellung des abgetasteten Signals im Zeitbereich als Multiplikation des Originalsignals mit einer Dirac-Impulsfolge der Impulsstärke 1 zu betrachten. Die Fourier-Transformation überträgt diese Operation in den Frequenzbereich. Die Spektren des Originalsignals und der Dirac-Impulsfolge werden hierbei im Frequenzbereich einer mathematischen Operation unterworfen, die der Multiplikation im Zeitbereich entspricht. Diese Operation heißt Faltung. Sie bewertet das Spektrum des Originalsignals mit dem durch den ganzen Frequenzbereich geschobenen Spektrum der Dirac-Impulsfolge. Wenn das Spektrum der Dirac-Impulsfolge zum Beispiel ein einzelner Dirac-Impuls wäre, würde die Faltung im Frequenzbereich als Ergebnis wieder genau das Spektrum des Originalsignals liefern.

 

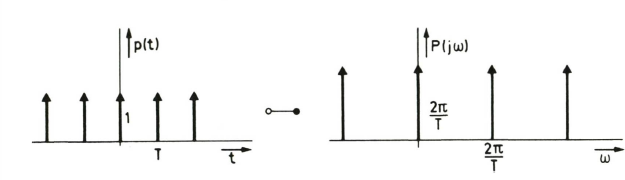
Die Fourier-Transformation des Impulskamms: Die Impulse des Spektrums befinden sich in einem Abstand gleich der Abtastfrequenz.

 

Das wahre Spektrum der Dirac-Impulsfolge errechnet sich mit Hilfe der Fourier-Transformation zu einer Dirac-Impulsfolge im Frequenzbereich, wobei sich die einzelnen Impulse in einem Abstand gleich der doppelten Grenzfrequenz zueinander befinden. Die Faltung des Originalsignal-Spektrums mit diesem Dirac-Impulsfolge-Spektrum führt auf ein Spektrum, das eine unendliche Aneinanderreihung von Original- Spektren darstellt, wobei die einzelnen Original-Spektren jeweils um die doppelte Grenzfrequenz zueinander verschoben sind.

Das Frequenzspektrum des abgetasteten Signals ist daher bis hin zur maximal zu übertragenden Grenzfrequenz identisch mit dem Frequenzspektrum des analogen Originalsignals. Oberhalb der Grenzfrequenz wiederholt sich die Originalspektralverteilung im abgetasteten Signal mit der doppelten Grenzfrequenz. Der sendeseitige Abtaster muß also mindestens mit der doppelten Grenzfrequenz arbeiten, da sich die wiederholten Einzelspektren des abgetasteten Signals andernfalls gegenseitig überlappen würden (Spiegelungseffekt). Der Empfänger kann das Originalsignal aus dem abgetasteten Signal dadurch zurückgewinnen, daß er die Spektralanteile oberhalb der Grenzfrequenz mittels eines Tiefpaßfilters abschneidet.

 

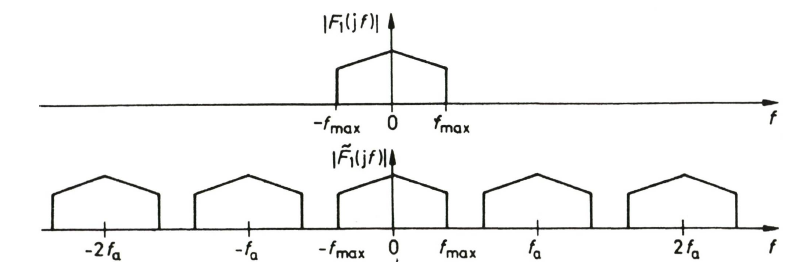
Das Spektrum des Originalsignals und des abgetasteten Signals: Das Originalsignal- Spektrum wiederholt sich im abgetasteten Signal mit der Abtastfrequenz.

 

16 Bit auf 14 Bit gepreßt

Das Problem liegt nur darin, wie man die mit 16 Bit quantisierten Abtastwerte in einer Wortlänge von 14 Bit Tunterbringt. Die Lösung liefert eine 16/14-Bit-Gleitkomma-Technik, die den 16-Bit-quantisierten Abtastwert der Rundfunkanstalt derart in ein 14-Bit-Wort wandelt, daß praktisch keine Dynamik verlorengeht. Dieses Verfahren unterteilt den gesamten Dynamikbereich in acht Pegelbereiche. Ein logischer Vergleicher stellt fest, in welchem dieser Pegelbereiche sich der höchste Signalwert von 64 aufeinanderfolgenden abgetasteten Signalpegeln befindet, indem er die Signale mit den Schwellwerten der verschiedenen Pegelbereiche vergleicht. Das Verfahren leitet aus diesem Pegelbereich einen Skalenfaktor mit 3 Bit Länge ab (23 = 8 Pegelbereiche), der alle 64 Abtastwerte übertragen wird. Das Besondere an diesem Verfahren ist, daß bei niederen und mittleren Signalpegeln das 14-Bit-Wort direkt die 14 niederwertigen Bits des 16-Bit-Abtastwertes übernehmen kann. Die beiden höherwertige Bits brauchen bei diesen Pegeln nicht übertragen werden, da sie = 0 sind.

 

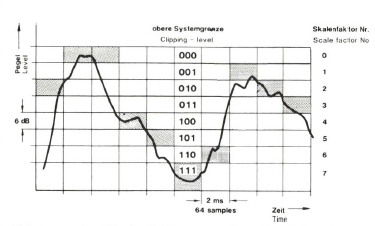
Ableitung des Skalenfaktors aus dem Quellsignal: Die Amplitudenauflösung erhöht sich von 14 auf 16 Bit bei mittlerer Aussteuerung. Bei Vollaussteuerung entspricht sie immerhin noch 15 Bit.

 

Fehlererkennung und -korrektur

Ein deutlicher Vorteil der digitalen gegenüber der analogen Rundfunkübertragung liegt in der Tatsache begründet, daß der Empfänger das binäre Signal am Empfangsort von Übertragungsfehlern befreien und damit wieder regenerieren kann. Bei analogen Übertragungsverfahren wirkt sich eine Übertragungsstörung direkt auf das analoge Signal aus. Bei der digitalen Übertragung bewirkt eine Störung dagegen die Änderung einzelner Bits der übertragenden Codeworte. Die wahren Werte der gestörten Bits kann der Empfänger unter Zuhilfenahme von mitübertragenen Fehlerkorrekturbits wieder zurückgewinnen. Bei der Satellitenübertragungsstrecke sendet man neben den eigentlichen Informationsbits zusätzliche Bits zur Übertragungsfehlererkennung und -korrektur. Dieser Fehlerbehandlung werden nur die 11 höherwertigen Bits eines Abtastwerts unterworfen, wobei die Abtastwerte von zwei Stereokanäle gemeinsam fehlergesichert werden, um die Zahl der Korrekturbits pro Stereoteilkanal zu verringern.

Der Sender erzeugt die Korrekturbits, indem er das 44-Bit-Wort der höherwertigen Bits von zwei Stereokanälen um 19 Bits erweitert und das so entstandene 63-Bit-Wort durch eine 19 stellige Dualzahl (Generatorpolynom vom Grad 19) teilt und den Divisionsrest der Länge 19 Bit als Korrekturbits in den 19 neu hinzugefügten Stellen übertägt, (Bose-Chaudhuri-Hocquenghem-(BGH (-Code 63,44). Die Empfängerseite teilt das gesamte übertragene 44+19 = 63-Bit-Wort in einem BCH-Decoder durch dasselbe Generatorpolynom. Bei fehlerfreier Übertragung muß der Divisonsrest = 0 sein, ansonsten kann der BCH-Dekoder bis zu 2 Fehler pro 63-Bit-Wort sicher korrigieren, bis zu 5 Fehler immerhin noch erkennen und den einzelnen gestörten 14-Bit-Worten durch ein interpolatives Verfahren den Mittelwert ihrer jeweiligen (zeitlichen) Nachbarworte zuweisen (Fehlerverschleierung).

 

Fehlerverschleierung durch Interpolation: Unbehebbare Fehler werden vertuscht. Dem fehlerhaft übertragenen Abtastwert wird der Mittelwert der Nachbar-Abtastwerte zugewiesen.

 

Glatte Unterschlagung - und trotzdem keine Strafe

Bei hohen Signalpegeln werden nur die 13 niederwertigen Bits und das höchstwertigste Bit, das Vorzeichenbit, im 14-Bit-Wort mitübertragen, dafür werden die beiden höherwertigen Bits, die dem Vorzeichenbit folgen, unterschlagen. Das ist aber nicht weiter Schlimm, da diese beiden höherwertigen Bits bei hohen Signalpegeln denselben Wert wie das Vorzeichenbit besitzen. Das Vorzeichenbit ist das höchstwertigste Bit des Codeworts, das den gesamten Dynamikbereich in eine positive und eine negative Hälfte unterteilt. Der Empfänger kann also das 16-Bit-Wort mit Hilfe des Skalenfaktors wieder aus dem 14-Bit-Wort rekonstruieren. Diese Methode erlaubt im Extremfall die Übertragung von bis zu 21-Bit-quantisierten Abtastwerten mittels 14-Bit-Worten.

Bei dieser Art der Kanalcodierung ist es möglich, neben den Fehlerschutzinformationen 11 kBit/s pro Stereokanal als Zusatzinformationen zu übertragen. Sie können direkt das Programm betreffen, wie zum Beispiel Zeitangabe, Art des Programms, Originallautstärke, oder Mitteilungen über die Quelle des Programmsignals liefern, etwa Titel der Sendung, Aufführungsort oder Komponist. 

 

Digitaler Hörfunk über Satellit (2. Teil)

Die Rundfunkübertragung via Satellit übermittelt 16 Stereo- bzw. 32 Mono-Rundfunkprogramme in einem rein digitalen Übertragungsverfahren. Die einzelnen Kanäle sind hierbei puls-code-moduliert, was bedeutet, daß ein Codierer den Abtastwerten der jeweiligen Originaltonsignale einen Zahlenwert im Zweiersystem zuweist, der die Amplitude des Abtastwertes repräsentiert. Die Darstellung des codierten Wertes im Zweiersystem ist vorteilhaft, da sie eine verhältnismäßig bequeme elektronische Realisierung erlaubt.

Das Zweiersystem, auch Dualsystem genannt, umfaßt nur die beiden Ziffern 1 und 0. Es läßt sich aber wie im normal gebräuchlichen Zehnersystem jeder beliebige Zahlenwert durch eine Kombination von Einsen und Nullen darstellen. Ebenso wie im Zehnersystem die Kombination etwa der Ziffern 3 und 7 die Zahl 37 erzeugt, erhält man im Zweiersystem durch die Kombination von beispielsweise der Ziffern 1 0 1 die Zahl 5. Die Zahlenwerte I und 0 lassen sich elektronisch durch zwei unterschiedliche Spannungspegel, etwa einem höheren Spannungswert (beispielsweise 5 Volt), der der logischen 1 entsprechen soll, und einem niederen Spannungspegel (0 Volt), der die logische Null realisiert, relativ einfach beschreiben.

 

An Baustellen bitte schneller fahren

Die Analog/Digital-Wandler in den Sendeanstalten erzeugen 16-Bit-quantisierte Abtastwerte, das bedeutet, daß sie jedem Abtastwert des analogen Originalsignals eine löstellige Dualzahl zuweisen, die die Amplitude des Abtastwertes in mathematisch verschlüsselter Form darstellt. Der Sender muß somit 16 Dualziffern pro Abtastwert in den Übertragungskanal schicken. Im Fachjargon nennen sich diese Dualziffern, also die logischen 1/0- Zustände, neudeutsch Bits. In die Welt der Elektronik übersetzt heißt dies, daß 16 Spannungspegelzustände (hoher oder niederer Pegel) zu übertragen sind. Um mit einem einzigen Übertragungskanal auszukommen, reiht der Sender die 16 Bits eines Abtastwertes zeitlich nacheinander an. Die Bitfolgen der aufeinanderfolgenden Abtastwerte des Originalsignals reiht er wiederum zeitlich aneinander zu „Bitströmen“. Natürlich muß bei der zeitlichen Aneinanderreihung der Bits der einzelnen Abtastwerte die Übertragungsgeschwindigkeit (Bitrate) entsprechend erhöht werden, da es sonst zu zeitlichen Verklemmungen kommen würde ähnlich einer Autobahnbaustelle, bei der die Fahrzeuge anstatt drei Spuren parallel lediglich eine einzige, dafür aber zeitlich aufeinanderfolgend (seriell) teilen.

 

 

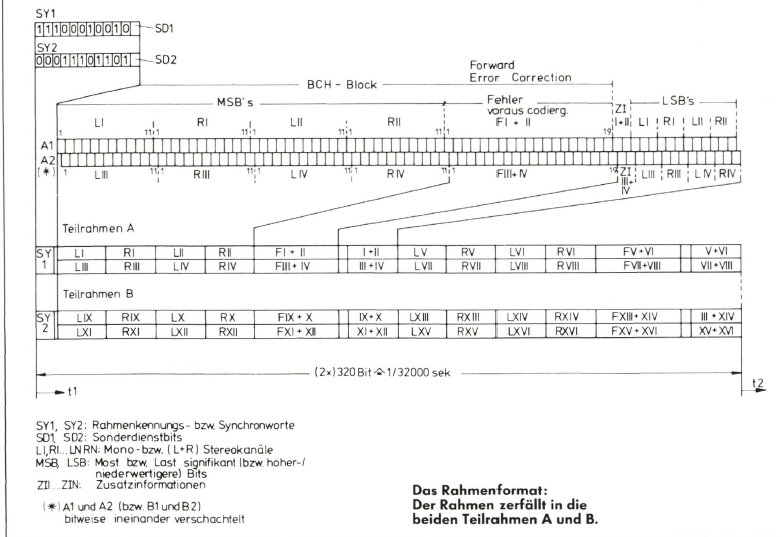
Die Blockbildung

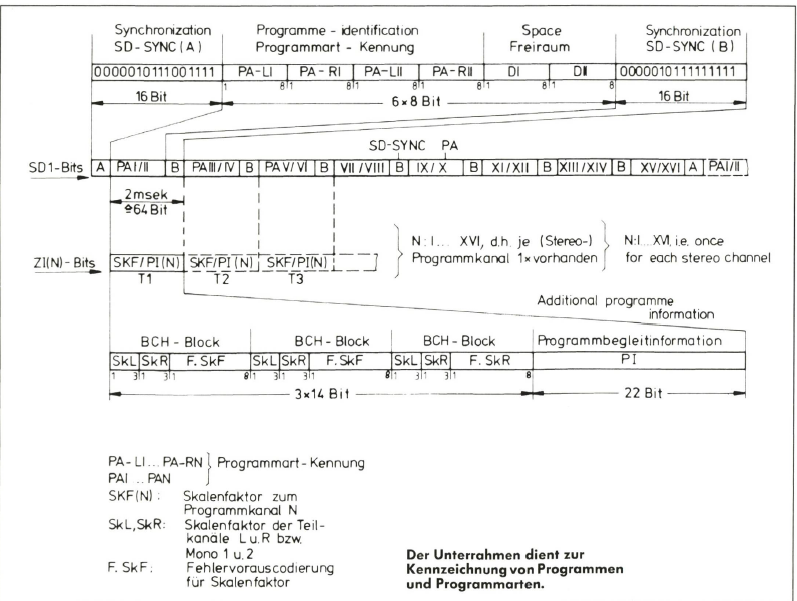
Die Fülle von Information, die in den Bitströmen über die Satellitenübertragungsstrecke gesendet wird, muß einer genau festgelegten Bedeutungs-Zuordnung unterliegen, damit der Empfänger genau weiß, welche Bedeutung jedem einzelnen Bit des Bitstroms zukommt. Hierzu faßt der Sender die Bits der einzelnen Teilinformationen in einem sogenannten Rahmen zu einer geordneten großen Gesamtbitfolge zusammen. Ein solcher Rahmen zerfällt aus übertragungstechnischen Gründen wiederum in zwei Teilrahmen, von denen jeder jeweils 4 BCH-Blöcke im Einzelbit-Zeitmultiplex enthält. Beim Einzelbit-Zeitmultiplex folgt abwechselnd je ein Bit des einen BCH-Blocks auf ein Bit eines anderen BCH-Blockes in zeitlich verschachtelter Reihenfolge. Jeder dieser BCH-Blöcke enthält die Information der Abtastwerte von zwei Stereokanälen, also vier Abtastwerte. Außerdem enthält jeder BCH-Block zwei Bits für Zusatzinformationen. Die Gesamtzahl der Bits eines BCH- Rahmens ist somit bei 16/14-Bit-Gleitkommatechnik mit einer Übertragungswortlänge von 14 Bit je Abtastwert die Summe aus 4x11 höherwertigen Bits, 19 Fehlerkorrekturbits, 4x3 niederwertigen Bits und 2 Zusatzinformationsbits, also zusammen.

 

Die Sonderdienstbits

77 Bits. Die beiden Teilrahmen enthalten bei dieser Anordnung zusammen 8 BCH-Blöcke bzw. 16 Stereokanäle. Damit der Empfänger aus der wilden Folge von Bits eine Information erkennen kann, muß er genau wissen, an welcher Stelle des Bitflusses ein Teilrahmen beginnt. Hierzu wird eine Synchronisationsbitfolge zu Beginn eines jeden Teilrahmens gesendet (Präambel). Sobald der Empfänger diese Bitfolge erkennt, weiß er, daß nun ein Teilrahmen beginnt. Die Synchronisationsbitfolge mit 11 Bit Länge ist so geschickt gewählt, daß die Wahrscheinlichkeit, daß zufälligerweise dieselbe Bitfolge irgendwo anders im Teilrahmen auftaucht und somit den Empfänger durcheinanderbringt, minimal ist. Zusätzlich wird pro Teilrahmen noch ein Sonderdienstbit (SD-Bit) übertragen. Die SD-Bits der jeweils ersten Teilrahmen von 512 aufeinanderfolgenden Hauptrahmen werden zu einem Unterrahmen zusammengefügt.

Dieser Unterrahmen enthält die Angaben über die Art der 16 übertagenen Stereoprogramme (Musik, Sport, Nachrichten ...), eine Mono/Stereokennung sowie eine Sprache/Musikkennung zum empfängerseitigen getrennten Abgleich von Sprach- und Musiklautstärke. Auch die beiden Zusatzinformationsbits, die pro BCH-Block anfallen, werden alle 2 Millisekunden zu einem Unterrahmen je Programmkanal von 64 Bit Länge zusammengefaßt, ln diesen Unterrahmen werden die 3-Bit-Skalenfaktoren, die bei der 16/14-Bit-Codierung entstehen, zum entsprechenden Decoder des Empfängers übertragen. Die Länge eines Teilrahmens errechnet sich hiermit aus der Summe von 4 BCH-Blöcken mit jeweils 77 Bit, 11 Synchronisationsbits und einem SD-Bit zu 320 Bit. Der Hauptrahmen besitzt also 640 Bits. Bei der benutzten Abtastrate von 32 kHz müssen somit 32000 x 640 Bit je Sekunde bzw. 20,48 MBit/sec pro Hauptrahmen übertragen werden.

Auf der Empfängerseite werden die Satelliten-Rundfunk-Empfangseinrichtungen (SRE) sowohl für Hör- als auch für Fernsehrundfunk verwendet. Die Parabolantenne der SRE empfängt das modulierte Digitalsignal auf einer Frequenz im Bereich von 11,7 bis 12,5 GHz. Das Hörrundfunksignal wird auf eine Zwischenfrequenz von 118 ± 7 MHz heruntergesetzt und ohne weitere Wandlung über das Anlagenverteilnetz den Rundfunkteilnehmergeräten zugeführt. Das hierbei verwendete Frequenzband von 111 bis 125 MHz mit den Sonderkanälen S 2 und S 3 hat die Bandbreite von zwei Fernsehkanälen und liegt über dem UKW- Frequenzband (das künftig bis auf 108 MHz ausgeweitet werden soll).

 

 

4-PSK-Modulation ermöglicht preiswerte Empfänger

Die drahtlose Übertragung des Digitalsignals erfordert die Umsetzung in eine höhere Frequenzlage durch Modulation einer hochfrequenten Trägerschwingung. Modulation bedeutet hier, daß das zu übertragende Digitalsignal die sinusförmige Trägerschwingung in einer oder mehreren ihrer Eigenschaften beeinflußt. Da das Digitalsignal nur zwischen festen Werten schwankt, verwendet man hier den Begriff „Tastung“ (Shift Keying) statt Modulation. Die Parameter des Trägersignals, die vom zu übertragenden Digitalsignal beeinflußt (umgetastet) werden können, sind die Amplitude, die Frequenz und die Phasenlage. Man spricht daher von Amplitudenumtastung (Amplitude Shift Keying, ASK), Frequenzumtastung (Frequency Shift Keying, FSK) und Phasenumtastung (Phase Shift Keying, PSK). Da das gewählte Frequenzband 111 bis 125 MHz nur eine Bandbreite von 14 MHz zur Verfügung stellt, muß ein Modulationsverfahren angewendet werden, das es ermöglicht, die 20,48 MBit/- sec eines Hauptrahmens mit einer Bandbreite von 14 MHz zu übertragen und einen preiswerten Demodulator im Empfänger zu verwenden. Am günstigsten eignet sich hierzu die 4-PSK-Modulation, mit der sich 1,5 Bit/sec je Hz übertragen lassen. Bei der vierstufigen Phasenmodulation (4-PSK = 4-Phase-Shift-Keying) wird das Digitalsignal in Form von vier Phasenwinkeländerungen des Trägers vom Sender zum Empfänger übertragen. Diese vier Phasenzustände werden den vier möglichen Kombinationen von zwei aufeinanderfolgenden Bits des Modulationssignals zugeordnet:

 

 

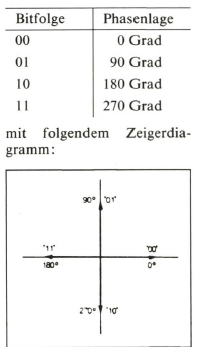
Diese Zuordnung entspricht einem Übergang vom Zweiersystem (Dualsystem) in das Vierersystem. Die vier Ziffern des Vierersystems werden durch die vier möglichen Phasenlagen dargestellt. Da hierbei zwei Bits in einem Doppelbit (Dibit) zusammengefaßt werden, ist die Schrittdauer eines Dibits gleich der zweifachen Schrittdauer eines Einzelbits bzw. die Dibit-Übertra- gungsbandbreite gleich der halben Einzelbit-Übertragungsbandbreite.

In der Praxis erreicht man immerhin noch die 0,65-fache Bandbreite der Einzelbitübertragung. Bei der praktischen Realisierung der 4-PSK werden zwei Dibit-Folgen aus dem binären Modulationssignal abgeleitet und auf zwei zueinander um 90 Grad phasenverschobene (orthogonale) Komponenten des Trägers durch Zweiphasenumtastung moduliert. Die Phasenlage des Trägers ist nun folgende:

 

 

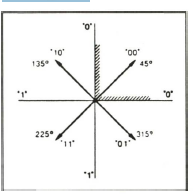
Der Empfänger muß zur Demodulation die richtige Absolutphase kennen. Er erschließt sie im Logikteil aus einem mitübertragenen Phasen-Synchronisierwort (Präambel).

 

Scrambling 

In große Schwierigkeiten kommen die Übertragungseinrichtungen des digitalen Rundfunks und auch die Empfänger bei logisch konstanten Bitfolgen, also bei einer längeren Folge von ausschließlich logischen Nullen oder Einsen. Dieser Zustand kann beispielsweise bei einer Modulationspause auftreten. Diese konstanten Bitströme verursachen im Frequenzspektrum des 4-PSK-modulierten Signals unschöne, stark ausgeprägte Spektrallinien. Diese wiederum verursachen zu ihrer Übertragung einen großen Mehrverbrauch an Sendeleistung.

 

 

Das Problem des Empfängers ist, daß er in der Lage sein muß, den Takt des übertragenen Digitalsignals aus den Bitfolgen zurückzugewinnen. Diesen Takt erkennt er aus den zeitlichen Abständen der logischen Eins/Null- Übergänge. Treten nun aber über längere Zeit keine Eins/Null-Übergänge auf, so schafft es der Taktrückgewinner nicht, die Zeitdauer der einzelnen Bits zu erkennen und daraus den Takt zu regenerieren. Es muß also vermieden werden, daß mehrere logische 1- oder 0-Zustände unmittelbar in Folge übertragen werden. Hierzu dient ein Scrambler, der die Bitströme in eine nahezu statistische Verteilung verwürfelt.

Diese Verwürfelung verhindert einerseits, daß im Spektrum des 4-PSK-modulierten Signals ausgeprägte Linien auftreten. Es wird daher keine Energie dazu verschwendet, Leistung zu übertragen, die praktisch keinen Informationsgehalt beinhaltet. Stattdessen ist die Leistung des 4-PSK-modulierten Signals dank dieser Energieverwischung gleich der Leistung des unmodulierten Trägers, lediglich die spektrale Verteilung der Leistung ändert sich. Der weitere positive Effekt dieser Verwürflung ist, daß der Taktrückgewinner nicht mehr auf konstante Bitfolgen stößt, die ihn aussteigen lassen. Die technische Realisierung der Verwürflung übernimmt ein Scrambling Generator. Er verwürfelt sämtliche Bits der beiden Doppel-Blockwörter jedes Hauptrahmens (308 der 320 Bits); die Synchronisationsworte und die Sonderdienstbits läßt er allerdings aus anwendungstechnischen Gründen unverändert. Da es dem Empfänger möglich sein muß, aus der verwürfelten Bitfolge die.

 

Coole Berechnung

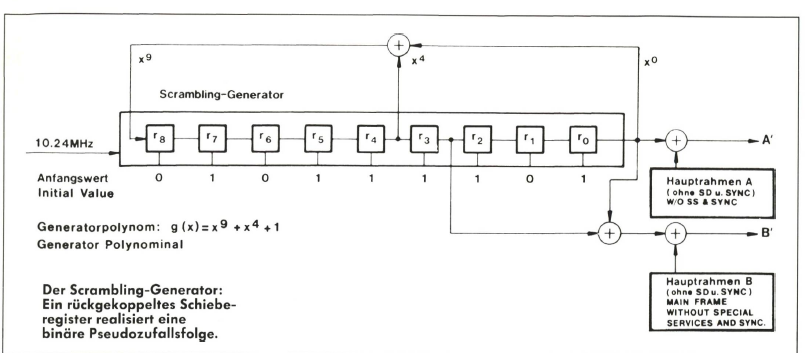
Originalbitfolge zurückzugewinnen, darf der Scrambling Generator natürlich keine wirklich zufällige, völlig unberechenbare Bitfolge erzeugen, denn sonst müßte der Entwürfler im Empfänger hellsehen können. Ganz so weit ist die Technik dann doch noch nicht fortgeschritten. Stattdessen erzeugt der Verwürfler eine Pseudozufallsfolge mit einer fest definierten Periode von 511 Bit und verknüpft die 308 Hauptrahmenbits mit dieser binären Pseudozufallsfolge. Ein Polynom 9. Grades beschreibt diese Zufallsfolge. Seine Realisierung geschieht mittels eines rückgekoppelten Schieberegisters. Der Scrambler wählt aus den 511 Taktschritten der Pseudozufallsfolge eine geeignete Folge von 308 Schritten aus, bei der die Wahrscheinlichkeit, daß die Verknüpfung dieser 308-Bit-Pseudozufallsfolge mit den Hauptrahmenbits zufälligerweise das Synchronisationswort erzeugt, möglichst gering ist, denn dies hätte zur Folge, daß der Empfänger ein falsches Rahmensynchronisationswort mitten im Rahmen erkennen würde.

Der Verwürfler setzt die neun Schieberegisterzellen auf den Anfangswert dieser 308-Bit-Zufallsfolge und verknüpft anschließend das erste Datenbit des Hauptrahmen A mit dem Inhalt der Zelle r0 und das erste Bit des Hauptrahmens B mit den Inhalten der Zellen r0 und r3 in einer modulo-2-Addition. Bei der Modulo-2-Addition ist das Ergebnis der Verknüpfung gleich Null, wenn die beiden Bits denselben Wert besitzen (also ergibt 1 -1 - 1 = 0 ). Haben sie unterschiedliche Werte, so ist das Ergebnis gleich 1. In dieser Weise werden sämtliche 308 Bits der beiden Hauptrahmen mit den 308 Bits der Pseudozufallsfolge zu einer Bitfolge verknüpft, die ebenfalls nur die Werte Eins und Null enthält.