Digitaltechnik

Hinter der so vielgefürchteten und bewunderten digitalen Computertechnik verbirgt sich eigentlich nur dumme Technik, allerdings davon recht viel. Rechnet ein digitaler Baustein 1 und 1 zusammen, so ergibt das 0. Das erscheint falsch, aber genau betrachtet fehlt hier nur der Übertrag. Das Ergebnis lautet exakt 10, was als Dualzahl der Dezimalzahl 2 entspricht. Digitale Bausteine (von Ausnahmen abgesehen) können nur mit den zwei Werten Null und Eins umgehen. Unsere üblichen Zahlen codiert der Computer erst anhand einer eingebauten Tabelle in eine Folge von Nullen und Einsen um, rechnet dann und wandelt schließlich wieder die „... 01001110000101110..." in lesbare Dezimalzahlen zurück. Und nur weil von den Transistoren so viele im Computer vorhanden sind und weil sie mehrmillionenfach in der Sekunde Einsen addieren, rechnet der Computer - entsprechend programmiert - dann doch alles Gewünschte blitzartig aus.

Der Technik erscheint ein verschlungenes Schriftzeichen viel zu kompliziert. Eindeutige Unterschiede, wie Spannung high oder low oder Loch im Streifen gestanzt oder nicht, können technisch sicher beherrscht werden. Bei der Compact Disc liegt die Information in mikroskopischen Erhebungen auf der Spiegelfläche. Der Laser fragt ab, ob eine Erhebung „vorbeifliegt“ oder der Strahl gerade von der Plattengrundebene reflektiert wird. Während der Fernschreiber mit fünf Nullen oder Einsen (Löchern) im Lochstreifen auskommt, nutzt der Computer achtstellige Codes, dafür schreibt er auch klein und groß, liefert problemlos „ö’s“ und „ü’s“ und viele Sonderzeichen vom # bis zum ß, und wenn lange genug auf der Tastatur „Klavier“ gespielt wurde, spuckt er auch solche Berichte wie diesen hier in seiner Funktion als Textverarbeitungsmaschine aus. Eine fünfstellige Dualzahl kann 25 Zustände darstellen, also 32 unterschiedliche Werte, acht Stellen ergeben 28, also 256 Möglichkeiten.

 

 

 

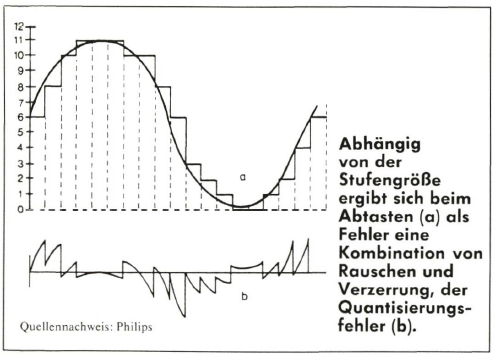
Analog - Digital

Digitus, lateinisch der Finger, digit, englisch die Ziffer. Digital also (mit den Fingern) abzählbar, was gleichzeitig auch in Stufen bedeutet. Nur volle Einheiten sind zählbar. Analog steht dagegen für kontinuierlich beeinflußbare Größen, die beliebig kleine Veränderungen ermöglichen, eine Größe wird durch eine andersartige dargestellt (Analogie), z.B. wachsender Schalldruck durch eine wachsende Spannung oder eine Rillenauslenkung (Plattenspieler). Analoge Systeme können geringe Anforderungen sehr preiswert erfüllen. Bei hohen Ansprüchen steigen die Kosten jedoch überproportional an.

Die diskrete (nichtkontinuierliche) Darstellung bei digitalen Systemen schafft eindeutigere Ergebnisse, die Stufung kann jedoch stören. Die Werte werden durch Zahlen dargestellt, die notwendigerweise dann bei Veränderungen mit dem kleinsten Stellenwert springen. Der dargestellte Wert gilt daher nur für einen bestimmten Augenblick. Zwischen den Zeiten, zu denen die Werte aktualisiert werden, ist keine Aussage über die tatsächliche Höhe machbar.

 

Abtasttheorem

Wird ein kontinuierlicher Vorgang nur durch kurze sich wiederholende Beobachtungen beschrieben, so beschreibt die Nachrichtentechnik das als einen Abtastvorgang. Bereits Kepler maß den Stand der Planeten nur von Zeit zu Zeit aus und konnte aber mit diesen Ergebnissen exakt die Bahn auch zwischen den Meßpunkten angeben. Wichtig - und hier ohne Probleme gegeben - war, daß er die Beobachtungen ohne Probleme mehrfach wiederholen konnte, noch bevor der Planet einen halben Umlauf geschafft hatte. Wie hätte er sonst erkennen können, in welcher Richtung der Planet die Sonne umläuft.

Beim Film klappt das nicht, die berüchtigten Speichenräder in den Wildwest-Filmen drehen rückwärts. Der Film schießt eine Momentaufnahme alle 1/25 Sekunde, und wenn die Speiche mehr als einen halben Speichenabstand (plus dem beliebigen Vielfachen eines ganzen Speichenabstandes) zwischen den Bildern zurücklegt, dann scheint sich das Rad rückwärts zu drehen. Nur aufwendige Systeme erlauben, solche Speichen als verwischte Scheiben abzubilden, so wie wir sie mit den Augen sehen würden. Das gleiche Prinzip gilt auch für das Stroboskop am Plattenspieler. Die Helligkeit netzgeführter Beleuchtung schwankt mit dem Doppelten der Netzfrequenz, daher müssen die Dunkelfelder sich alle 1/100 Sekunde genau um eine Position weiterbewegt haben. Deshalb ergab sich auch exakt 33 1/3 min für die Drehzahl, entsprechen genau 180 Strichen bei 50 Hz (216 bei 60 Hz). 33 min hätte dagegen 181,8181 Striche ergeben.

Der Mathematiker Shannon hat bewiesen, daß ein sich wiederholendes Signal eindeutig (und genau) rekonstruiert werden kann, wenn die Daten mindestens zweimal je Wiederholzyklus bestimmt werden. Ein 20-Kilohertz-Ton muß also schneller als mit 40 kHz abgetastet werden, für das CD-System gilt mit geringem Sicherheitsabstand 44,1 kHz (die Studiotechnik arbeitet lieber mit 48 oder 50 kHz). Jede Frequenz oberhalb 22,05 kHz läuft damit „rückwärts“ (wird gespiegelt, Aliasing). Und damit ein solches System kein 44-kHz-Eingangssignal als 100 Hz ausgibt, werden diese Frequenzbereiche durch aufwendige Anti-Aliasing-Tiefpaßfilter entfernt. Solche Aliasing-Störtöne fallen leicht auf und stören weitaus mehr als die verrückten Speichen im Film.

 

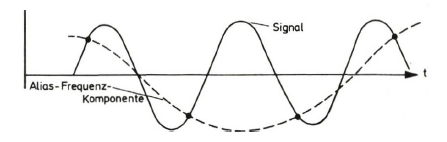
Wird ein Signal zu selten abgetastet (-► Punkte), entsteht der Eindruck einer tieferliegenden Signalfrequenz.

 

Bitte 8 bit 

Eine duale Information ist 1 bit, acht davon heißen ein Byte und stehen im Normalfall für ein Schriftzeichen. Verwechslungen sind üblich. Der Computer codiert ein „i“ mit 0 1001 und ein „y“ mit 1 1001. Setzt er ein Bit falsch, so wird aus Byte Bite. Eine HiFi-Musikaufzeichnung benötigt für die Zahlendarstellung mindestens 14 bit. 16 bit sind üblich, und von einer 18-bit-Aufzeichnungs-Möglichkeit träumen Studioleute.

 

Kopieren, ob schwarz oder weiß, legal oder als Pirat

Der wohl wichtigste Vorteil von Digitalaufzeichnungen besteht in ihrer uneingeschränkten Kopierbarkeit. Gegenüber der nicht zu vernachlässigenden Qualitätsverschlechterung bei der Überspielung von Analogbändern erlaubt PCM durch die dazwischen geschaltete Fehlerkorrektur Kopien, die im Idealfall sogar eine geringere Fehlerhäufigkeit als das Original haben. Da immer einige wenige unkorrigierbare Fehler vorhanden sind, kann dann allerdings doch eine (minimale) Verschlechterung eintreten. Das Kopieren von PCM-Aufnahmen ohne Fehlerkorrektur ist nicht zu empfehlen (im Videoformat möglich), da sich hierdurch die Fehlerhäufigkeit drastisch erhöht und zum vollständigen Ausfall des Systems führen kann (Muting). Im professionellen Bereich wird durch mehrfaches Überspielen, bevor die endgültige Schallkonserve erstellt wird, einiges an Verschlechterung hingenommen. Erst die Digitaltechnik hat auch im analogen Bereich die Verschlechterung durch die ungehemmte Kopierlust deutlich gemacht. Das erste Originalband muß gar nicht soviel schlechter sein als eine Digitalaufnahme, zumindest was den Rauschabstand betrifft.

 

Zahlenmeister 

 

 

 

82 DM auf 14 bit quantisiert 

16-bit-Datenwörter können einen Zahlenbereich von 65 536 abdecken (216). Wechselspannung bedingt, daß auch negative Größen erfaßt werden müssen, es können also ganze Zahlen von -32 768 bis +32 767 dargestellt werden. Einen Buchhalter würde ein 16-bit-Datenwort noch nicht zufriedenstellen. Bei einer Genauigkeit von 1 Pfennig könnte er gerade noch 320 DM = Euro genau verbuchen. Ständen nur 14 bit zur Verfügung, so erfolgt die Buchung entweder nur noch in Stufungen von 4 Pfennig, oder der Wertebereich hört bereits bei 8192 Pfennigen entsprechend ungefähr 82 DM = Euro auf.

Da für Super-HiFi 16 bit 44 000 mal in der Sekunde in Stereo mit 50% Redundanz gespeichert werden müssen, ergibt das einen Datenstrom von: 16 • 44 000 • 2 • 1,5 bit = 2,1 Megabit je Sekunde. Das sind in der Computereinheit Byte 260 Kilobyte je Sekunde. Ein Heimcomputer mit 64KB ist dann in einer Viertelsekunde voll, eine Diskette in knapp einer Sekunde. Selbst ein Bürocomputer mit einer 10 Megabyte fassenden Hard-Disk- oder Winchester-Speichereinheit würde gerade 38 Sekunden Stereomusik verkraften. Da verwundert es um so mehr, daß eine Compact Disc 1 Gigabyte (oder 8 Gigabit) Musikdaten speichern kann, ein 8-Stunden- PCM-Pseudovideoband kommt übrigens auf 8 Gigabyte (oder 64 Gigabit), für Computerleute eine Zahl zum Träumen.

 

Digital geblinzelt

 

 

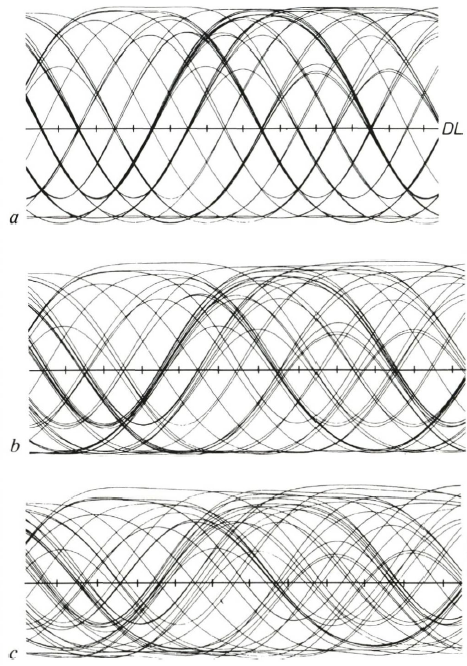
Diesen Signalverlauf liest die Laser-Einheit von der Compact Disc. An jeder Zeitmarke (Kreuze auf der DL-Geraden) wird festgestellt, ob das Signal ober- oder unterhalb der Entscheidungsschwelle liegt.

a. Das obere Signal ist in Amplitude und Zeit sauber, Einsen und Nullen werden klar mit Sicherheitsabstand erkannt.

b. Abstandsänderungen zum Linsensystem führen bereits zu verschlechterten Amplituden und damit drastisch verminderten Sicherheitsabständen.

c. Ist die CD auch noch zusätzlich leicht verzogen (Winkel 1,2°), so treten zusätzlich Zeitfehler (Jitter) auf. Die Augen, in denen die Entscheidungspunkte (Kreuze) möglichst mittig liegen sollten, schließen sich. Einige der Kurven laufen sogar an der falschen Seite dieser Punkte vorbei und werden daher falsch erkannt. In Englisch heißen solche Oszillogramme Eye Pattern (Augen-Muster). Diese Art der Darstellung hilft bei Justage und der schnellen Qualitätsbeurteilung.

 

Sehr gut, trotz Fehlern im Diktat

Die Fehlerkorrektur stellt den wesentlichen Vorteil der Digitaltechnik dar. Der Datenstrom kann verfälscht oder sogar unterbrochen werden, Recheneinheiten regenerieren alles wieder vom Original nicht unterscheidbar. Analogen Systemen fehlt diese Möglichkeit, der Ton ist dann für immer gestört, aufwendige Filter oder geschicktes Schneiden beim analogen Tonband können Fehler stark mildern. Eine dem Original gleiche Version kann bei der Restauration nicht mehr erzeugt werden.

Eine Korrekturmöglichkeit erfordert aber, daß etwas mehr Information übertragen wird, als eigentlich minimal notwendig ist. Wer aufgrund eines falsch angegebenen Datums einen Termin versäumt hat, wird es begrüßen, wenn zusätzlich zum 1. August 1985 noch der Wochentag (Donnerstag) angegeben ist. Diese Redundanz (eigentlich überflüssige, da von jedem anhand eines Kalenders leicht nachprüfbare Information) ermöglicht eine Fehlererkennung (wenn auch keine -korrektur). Stimmen die Daten nicht zueinander, so ist das Jahr, der Monat oder der Tag falsch. Solche Fehlererkennung kann aber auch versagen, wie im Februar/März in drei von vier Jahren. Hier fällt der gleiche Wochentag auf die Tageszahl. Aber immerhin können viele Fehler erkannt und dann durch Nachfrage ausgeräumt werden. Die Korrektur erfordert einige Denkarbeit. In der Schrift kann vieles aus dem Zusammenhang erahnt werden, wieviele Briefe wären sonst unleserlich, von den berüchtigten Arztrezepten und den Graphologen in der Apotheke ganz zu schweigen. Fehlerfrei läßt sich der Satzteil „H*Fi- Ver*tär*er u*d La**sprech*r . . .“ verstehen. Zur Fehlerkorrektur dienen Kenntnisse der deutschen Sprache und der HiFi-Technik.

Fehlt aber zuviel, wie in „Compact**s****e*marke“, so kann es statt „Compactcassettenmarke“ auch „Compaktdiscindexmarke“ lauten. Das Prinzip der Fehlerkorrektur läßt sich mit einem Pkw-Fahrtenbuch erklären. 

 

 

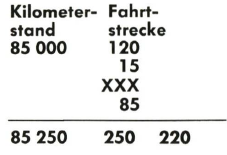
(XXX = nicht notiert oder unleserlich) Um die Strecke XXX zu rekonstruieren, kann die sauber notierte Gesamtstrecke = 220 km und der Fahrweg anhand des Kilometerstandes = 250 km verglichen werden. Die gesuchte Strecke kann daher zu 30 km abgerechnet werden.

Voraussetzung für diese Korrektur ist die Kenntnis, wo der Fehler steckt. Wäre statt XXX 55 km verzeichnet, so könnte der Fehler von 25 km in allen Zeilen zu finden sein. Wurde aber der Fahrtzweck in jeder Zeile verzeichnet, so schränkt sich der Fehlerort ein, da einige Entfernungen auf 20 km genau bekannt sein werden. Ist jedoch das Fahrtenbuch fahrlässig geführt, so sind gleich mehrere Fehler zu erwarten. Dann versagt die oben angegebene Methode. Aber auch hier gäbe es Korrekturverfahren. Um im Beispiel zu bleiben, könnte zumindest über längere Distanzen anhand des Spritverbrauches ein Fehler beseitigt werden (im Beispiel allerdings nur näherungsweise).

 

Fehlerkorrekturdaten der Compact Disc

Üblicherweise kann mit 1 bit Fehler auf 10 000 bis 1000 bit ab Abtastlaser gerechnet werden. Die Fehlerverdeckung muß im ersten Fall nur einmal in 10 Stunden eingreifen, alles andere wird voll korrigiert. Bei der um Faktor 10 erhöhten Fehlerrate steigt allerdings die Interpolationshäufigkeit um den Faktor 600 000 auf 16 mal in der Sekunde an. Damit wird allerdings erst durchschnittlich jeder 5000ste Wert ungenau. Die wirklich als Klick hörbaren unerkannten Fehler betragen auch dann noch unter 1 in 1 Monat. Da aber nach dem Murphyschen Gesetz das Unwahrscheinliche bevorzugt in wichtigen Situationen eintritt, gibt es doch Compact Discs, die auf manchen Spielern hörbare Fehler aufweisen. Gerade die Aussetzer „erfreuen“ besonders, die gerade mitten in einer Bandüberspielung auftraten und erst dann erkannt werden, wenn die entliehene CD wieder außer Haus ist. Aber es ist ja schließlich auch nur das Aufnehmen der eigenen CDs zum privaten Gebrauch gestattet. Kritischer sind da die Live-Aufnahmen auf PCM-Recorder. Wer möchte da nicht nach einem solchen Mißgeschick die ganze PCM-Digitaltechnik in die Ecke werfen. Da hilft nur 100 Prozent Redundanz, in Form eines zweiten Recorders. Nicht wenige Teilstücke professioneller „Digital“-Aufnahmen wurden schon mit Hilfe einer mitlaufenden Analogmaschine gerettet.