Warum bedeutet Farbe eigentlich Licht? Was ist der Mensch in der Lage, überhaupt wahrzunehmen? Im folgenden Artikel mit freundlicher Unterstützung der Fachzeitschrift ELV sind die wichtigsten Begriffe rund um das Thema Licht und Beleuchtung zusammengetragen.
Lichttechnische Grundlagen
Licht ist die Grundlage unseres Lebens. Die gewaltigste, seit der Existenz unseres Planeten vorhandene Lichtquelle ist die Sonne. Ohne sie wäre die Erde eine kalte Wüste ohne Flora, Fauna und Atmosphäre. Denn Licht und Wärme sind die Voraussetzungen der Photosynthese und damit von sauerstoffbildendem Pflanzenwachstum als Existenzvoraussetzung für Mensch, Tier und Pflanzen. Vor Urzeiten, als der Mensch noch nicht über Feuer oder andere Lichtquellen verfügte, war er auf die Sonne als wärmende, erhellende Quelle am Himmel angewiesen. Erst als er selbst Licht erzeugen konnte, waren ihm Bergbau, nächtliche Aktivitäten und andere zivilisatorische Leistungen möglich. Doch mit kaum einem Phänomen hat der Mensch so viele Schwierigkeiten, es umfassend zu erklären und seine Wirkungen auf Körper, Geist und Psyche zu beschreiben.
Die moderne Physik hat durch zahlreiche Experimente nachgewiesen, dass Licht zwei – in letzter Konsequenz durchdacht – unvereinbare Wesensmerkmale hat. Manche Wirkungen des Lichts lassen sich nur erklären, wenn man seinen Wellencharakter voraussetzt, andere erfordern zwingend seine Partikelstruktur. Dieser Dualismus zwischen (elektromagnetischer) Welle und (geladenem) Teilchen ist bis heute noch nicht durch eine übergeordnete, geschlossene Theorie befriedet. Wir wollen in diesem Artikel unter Licht denjenigen Teil des elektromagnetischen Spektrums verstehen, den unsere Augen wahrnehmen können.
Das elektromagnetische Spektrum
Elektromagnetische Strahlung sind elektromagnetische Wellen, die aus gekoppelten elektrischen und magnetischen Feldern bestehen. Ihr Spektrum erstreckt sich von Längstwellen mit mehreren tausend Kilometern Wellenlänge bis zu höchstfrequenten kosmischen Strahlungen mit weniger als 10–15 m (10–15 m = 1 Femtometer) Wellenlänge.
Die Frequenz der elektromagnetischen Strahlung ist über Gleichung 1 mit ihrer Wellenlänge und der Lichtgeschwindigkeit verbunden.

Das sichtbare Spektrum
Schon Goethe hatte vor 200 Jahren in seiner Farbenlehre gesagt: „Das Licht überliefert das Sichtbare dem Auge, das Auge überliefert’s dem ganzen Menschen.“ Damit hatte er voll ins Schwarze getroffen. Denn das Auge ist tatsächlich eine Empfangseinrichtung für elektromagnetische Strahlung, allerdings nur für einen kleinen Ausschnitt daraus – das sichtbare Licht.
Das sichtbare Lichtspektrum (Bild 1) beginnt vom Infrarot (Wärmestrahlung) kommend bei einer Wellenlänge von etwa 780 nm und geht bei 380 nm in Ultraviolett über. Mit Gleichung 1 errechnen sich die zugehörigen Frequenzen zu 384,3 THz bzw. 788,9 THz (1 THz = 1012 Hz). Ganz exakt lassen sich diese Grenzwerte nicht angeben, weil die Eigenschaften des menschlichen Auges von Mensch zu Mensch variieren.
Die wichtigsten Spektralfarben sind Rot (780–640 nm
bzw. 384–468 THz) über Orange (640–600 nm bzw. 468–500 THz), Gelb (600–570 nm bzw. 500–526 THz), Grün (570–490 nm bzw. 526–612 THz), Blau (490–430 nm bzw. 612–697 THz) bis zu Violett (430–380 nm bzw. 697–789 THz).
Das menschliche Auge hat seine maximale Empfindlichkeit beim helladaptierten Sehen (Tagsehen) im Bereich von 555 nm (Gelb-Grün). Dieses Empfindlichkeitsmaximum verschiebt sich mit zunehmender Dunkelheit (Nachtsehen) bis zu 510 nm (Blau), weil dafür andere Rezeptoren in der Netzhaut ins Spiel kommen.
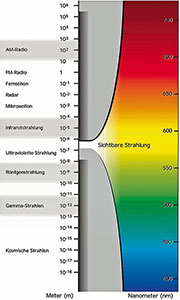
Bild 1: Vom gesamten Spektrum der elektromagnetischen Strahlung ist der sichtbare Anteil nur ein winziger Teil. (Quelle: Philips)
Bild 2 zeigt die auf einen Maximalwert von 1 normierten Empfindlichkeitskurven V(λ) des Auges für Tag- und Nachtsehen. Die nicht normierten Kurven werden auch als photometrisches Strahlungsäquivalent bezeichnet. Ihre Maximalwerte betragen 683 lm/W für Tagsehen und 1699 lm/W für Nachtsehen. Dies muss bei der Bewertung des sichtbaren Lichts berücksichtigt werden und schlägt sich in den fotometrischen Einheiten für den Lichtstrom Lumen (lm) und die Lichtstärke Candela (cd) nieder. Nicht sichtbare Strahlung hingegen wird durch strahlungsphysikalische Einheiten wie Strahlungsdichte (Watt/Sterad) u. a. beschrieben. Wir wollen auf die lichttechnischen Größen im Folgenden genauer eingehen.
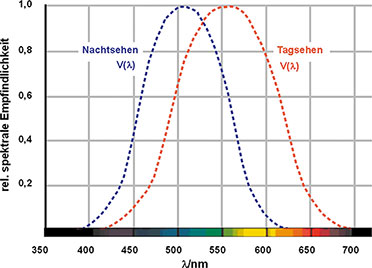
Bild 2: Für Tag- und Nachtsehen kommen beim Auge zwei Arten von Rezeptoren mit unterschiedlicher spektraler Empfindlichkeit zum Einsatz.
Sterad
Bei der Definition lichttechnischer Größen spielt der Steradiant, auch Sterad (srad, sr) genannt, eine wichtige Rolle. Er ist definiert als ein Teil der Oberfläche einer Kugel, dividiert durch das Quadrat des Kugel-radius. Der Begriff lässt sich veranschaulichen, wenn wir eine Kugel mit dem Radius r betrachten. Der Sterad beschreibt nun einen vom Mittelpunkt der Kugel aus gemessenen Raumwinkel, der eine gewisse Fläche A aus der Kugeloberfläche ausschneidet. Ein Raumwinkel von 1 sr umschließt auf der Oberfläche einer Kugel mit Radius 1 m eine Fläche von 1 m². Weil die Oberfläche dieser Kugel 4 π r² = 4 π m² beträgt, hat die gesamte Kugel einen Raumwinkel von 4 π sr. Bild 3 soll dies veranschaulichen. Darin sehen wir eine Kugel mit Radius r, in welcher der ebene Öffnungswinkel einen Konus beschreibt, dessen Kappe die Fläche A hat.
Der Zusammenhang zwischen dem ebenen Öffnungswinkel und dem Raumwinkel Ω ist in Gleichung 2 abgeleitet.
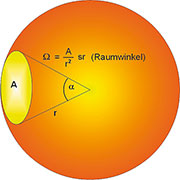
Bild 3: Der Raumwinkel O ist im Dreidimensionalen das Gegenstück zum ebenen Winkel a. Er ist der Quotient aus einem Teil einer Kugeloberfläche und dem Radius im Quadrat.

In Tabelle 1 sind einige Werte für berechnet.

Lichtstrom, Lumen
Mit der Einheit Sterad (sr) für den Raumwinkel lassen sich die wichtigsten lichttechnischen Größen als physikalische sowie unter Berücksichtigung der Farbempfindlichkeitskurve des Auges als physiologische Größen mit ihren jeweiligen Einheiten beschreiben. Eine Zusammenstellung der wesentlichen Größen zeigt die Tabelle in Bild 4. Dabei muss man wissen, dass bei der höchsten Empfindlichkeit des hellsehenden Auges (555 nm) eine Strahlungsleistung von 1 W einem Lichtstrom von 683 Lumen entspricht. Die Strahlungsleistung bei anderen Wellenlängen ist entsprechend der normierten Empfindlichkeitskurve V(λ) in einen äquivalenten Lichtstrom umzurechnen. 
Der Lichtstrom (auch Strahlungsfluss genannt), gemessen in Lumen (lm), ist das physiologische Gegenstück zur physikalischen Strahlungsleistung (gemessen in Watt). Er berücksichtigt die Empfindlichkeits-kurve des Auges, die oft mit dem Formelzeichen V(λ) bezeichnet wird und eine Funktion der Wellenlänge ist. Diese wird mit dem spektral verteilten energetischen Lichtstrom e(λ) multipliziert und wichtet ihn damit wellenlängenabhängig. So ist die Definitionsgleichung für den gesamten Lichtstrom v über das Sehspektrum plausibel
(Gleichung 3).
Man beachte, dass die Indizes v für visuell und e für energetisch stehen.
Für monochromatisches Licht (z. B. eines Lasers) der Wellenlänge λmono vereinfacht sich Gleichung 3, weil es jetzt nur noch eine Frequenz zu berücksichtigen gibt. Dadurch wird das Integral überflüssig (Gleichung 4).![]()
Lichtstärke, Candela
Die Lichtstärke Iv ergibt sich gemäß Gleichung 5 als Quotient aus Lichtstrom v in lm und durchstrahltem Raumwinkel Ω in sr (vergl. Bild 3). 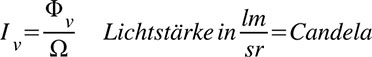
Eine Haushaltskerze gibt näherungsweise ihr Licht gleichmäßig in alle Richtungen des Raums ab (isotroper Strahler). Bei einem Lichtstrom v von ca. 12 lm, verteilt über den vollen Raumwinkel 4 π sr ≈ 12 sr, ergibt sich nach Gleichung 5 eine Lichtstärke von ca. 1 lm/sr, was den Begriff Candela (Kerze) erklärt.
Die Lichtstärke ist unabhängig vom Abstand zur Lichtquelle. Sie hängt ausschließlich vom durchstrahlten Raumwinkel ab und berücksichtigt dabei ein unterschiedliches Abstrahlverhalten der Lichtquelle in verschiedene Richtungen. Dieses kann beispielsweise durch einen Reflektor oder eine Bündelungsoptik bewirkt werden.
Beleuchtungsstärke, Lux
Während die Lichtstärke beschreibt, wie viel Lichtleistung (Lichtstrom) in einen bestimmten Raumwinkel abgestrahlt wird, sagt die Beleuchtungsstärke Ev, aus, wie viel davon auf einer bestimmten Fläche A ankommt. Sie ist also eine sehr sinnvolle empfangs-bezogene Größe, denn es interessiert z. B. weniger, welcher Lichtstrom eine Deckenlampe im Büro verlässt, sondern ob dadurch eine Schreibtischoberfläche gut ausgeleuchtet wird. Das führt zur Definition der Beleuchtungsstärke gemäß Gleichung 6.
Die Beleuchtungsstärke Ev nimmt im Quadrat des Abstands zur Lichtquelle ab, wogegen die Lichtstärke Iv unabhängig vom Abstand zur Lichtquelle ist.
Um ein gewisses Gefühl für die abstrakte Größe „Beleuchtungsstärke in Lux“ zu entwickeln, sollte man sich die Tabelle in Bild 5 gut ansehen und einige wichtige Werte einprägen. Damit kann man ungefähr einordnen, welchen Lichtverhältnissen ein bestimmter Lux-Wert entspricht. Die Tabelle macht den gewaltigen Dynamikumfang des menschlichen Auges deutlich. Es ist anschaulich, dass die Neigung der beleuchteten Oberfläche gegenüber dem einfallenden Licht eine Rolle für deren Beleuchtungsstärke spielt. Am höchsten ist die Beleuchtungsstärke, wenn das Licht senkrecht auf die beleuchtete Fläche auftrifft. 
Abweichungen vom rechten Winkel führen zu einem Rückgang der Beleuchtungsstärke nach der Kosinusfunktion (Bild 6). Bei Luxmetern ist deshalb oft ein Kosinusdiffusor vor dem Messsensor angebracht, um die Winkelabhängigkeit einer Messung zu reduzieren.
Um die durchschnittliche Beleuchtungsstärke in einem Raum zu ermitteln, muss seine Grundfläche in mehrere gleich große, möglichst quadratische Gebiete eingeteilt werden. 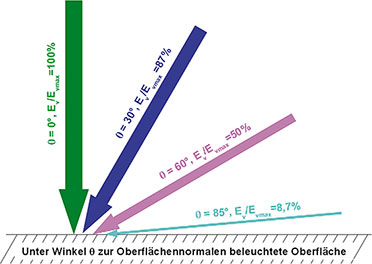
Bild 6: Die Beleuchtungsstärke hängt davon ab, unter welchem Winkel die Lichtstrahlen auf die beleuchtete Fläche treffen.
Dann wird die Beleuchtungsstärke in der Mitte jedes Quadrats gemessen und der Durchschnitt der Ergebnisse ermittelt. Die Mindestzahl an Gebieten bestimmt die Genauigkeit der Messung. Sie wird über die Zahl n gemäß Gleichung 7 und der darin enthaltenen Tabelle berechnet (Quelle: Benning GmbH & Co. KG, Bocholt). 
Beispiel: Für einen Raum mit den Grundmaßen 5 x 6 m und einem Abstand zwischen Mess- und Leuchtmittelebene von 1,8 m berechnet sich n zu 1,5. Daraus folgt, dass für eine 5%ige Genauigkeit der gemittelten Beleuchtungsstärke an 18 Stellen gemessen werden muss.
Leuchtdichte
Reale Lichtquellen sind nicht punktförmig, sondern haben eine gewisse Ausdehnung (Bild 7). Die vollständige, in eine Richtung ausgesandte Lichtstärke ist dann die Summe der Beiträge der einzelnen Flächenelemente der Lichtquelle. Für jedes dieser Flächenelemente kann man nun die sogenannte Leuchtdichte angeben. Dabei ist dA' = dA cos() die scheinbar leuchtende Fläche, weil sie senkrecht zu den Sehstrahlen steht.
Bild 7: Die Glühlampe mit mattiertem Glas sendet von jedem Bruchteil ihrer Oberfläche einen Beitrag zum gesamten Lichtstrom, der das Auge des Betrachters erreicht.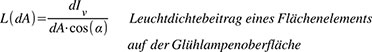
(Gleichung 8).
Werden alle Leuchtdichtebeiträge im für den Beobachter sichtbaren Bereich der Glühlampe aufintegriert, erhält man deren gesamte Leuchtdichte.
Wenn die Leuchtdichte eines Strahlers vom Betrachtungswinkel unabhängig sein soll, muss die Lichtstärke (wie an Gleichung 8 zu sehen) eine kosinusförmige Abhängigkeit vom Blickwinkel haben (Gleichung 9). Ein derartiger Strahler (Lambert-Strahler) ist z. B. eine von hinten beleuchtete Milchglasscheibe, die das durchgeleitete Licht vollkommen diffus streut.![]()
Gleichung 9
Das Strahlungsverhalten eines Lambert-Strahlers zeigt Bild 8. Der gesamte Lichtstrom eines Lambert-Strahlers ergibt sich durch Integration der Lichtstärke über den vor ihm liegenden Raum zu v = π Ivmax.
Die Leuchtdichte ist ein Maß für die Helligkeit einer Lichtquelle. Dem Auge scheint eine konzentrierte Lichtquelle (Leuchtdiode) heller als eine ausgedehnte (Glühlampe), auch wenn beide die gleiche Lichtstärke haben. Damit beide Lichtquellen den gleichen Helligkeitseindruck erzeugen, muss deren Lichtstärke erst auf die Licht emittierende Fläche bezogen werden und dabei zu einem gleichen Wert führen. Wie schon gesagt, ist die Leuchtdichte L der Quotient aus Lichtstärke und ausstrahlender Fläche (Gleichung 10). 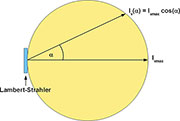
Bild 8: Der Lambert-Strahler zeigt sich unter jedem Blickwinkel mit der gleichen Leuchtdichte. Voraussetzung ist die kosinusförmige Abhängigkeit der Lichtstärke vom Blickwinkel.
Gleichung 10
Strahler mit gleicher Leuchtdichte emittieren den gleichen Lichtstrom aus einem gleich großen Teil ihrer Oberfläche (oder einen doppelt so großen Lichtstrom aus einer doppelt so großen Fläche) und werden deshalb als gleich hell empfunden.
Ein Beispiel: Die Helligkeit eines Monitor-Displays mit einer Fläche von 0,25 m² wird mit 1000 cd/m² angegeben. Das Display strahlt demnach mit 250 Candela in den Raum. Ein Display mit der doppelten Fläche müsste also mit der doppelten Candelazahl abstrahlen, um ein gleich helles Bild zu haben.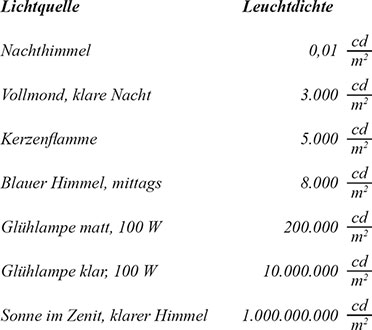
Die Tabelle in Bild 9 gibt einen Überblick über verschiedene Lichtquellen und ihre Leuchtdichten.
An einem weiteren Beispiel wollen wir unser Verständnis vertiefen. Die Sonne emittiert mit einer Fläche von A = πD²/4 in Richtung Erde. Die Sonne hat einen Durchmesser von D = 1,4 Mio. km und „zeigt“ uns eine Fläche von A = 1,5394 x 1012 km2. Bei senkrechter Einstrahlung und klarem Himmel beträgt die Beleuchtungsstärke 100.000 Lux (vergl. Bild 5). Die restliche Rechnung demonstriert Gleichung 11: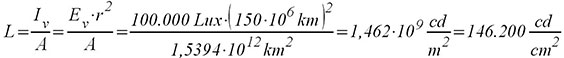
Dieser Wert stimmt recht gut mit dem in Bild 5 mit 100.000 cd/m² angegebenen überein, denn bei unserer Rechnung haben wir keinerlei Dämpfung des Sonnenlichts im interstellaren Raum und durch die Erd-atmosphäre angenommen, wodurch der berechnete Wert etwas höher ausfällt.
In Bild 10 ist der Unterschied zwischen Beleuchtung und Leuchtdichte noch einmal veranschaulicht. Die Beleuchtung beschreibt die Lichtverhältnisse am bestrahlten Objekt, die Leuchtdichte die Strahlungsstärke der Lichtquelle bezogen auf ihre emittierende Fläche.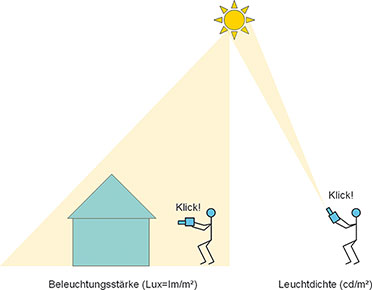
Bild 10: Die Beleuchtungsstärke beschreibt die Lichtverhältnisse am beleuchteten Objekt, die Leuchtdichte sagt uns, unter welcher Helligkeit uns die Lichtquelle erscheint.
Bild 11 belegt qualitativ, dass der Helligkeitseindruck von der Leuchtdichte abhängt. Wir sehen hier eine Energiesparlampe mit 12 W Leistungsaufnahme (links) und eine LED mit etwa 70 mW (rechts). Obwohl die LED nur ein knappes Prozent der Leistung der Energiesparlampe aufnimmt, kann sie beim Helligkeitseindruck mithalten, weil sie ihren vergleichsweise schwachen Lichtstrom über eine kleine Fläche aussendet. Ein weiteres Beispiel sind Laser-Pointer (Lichtzeiger für Vorträge) der Klasse 2 mit maximal 1 mW Strahlungsleistung. Diese wird als Licht aus einer winzigen Emissionsfläche abgestrahlt. Durch den extrem kleinen Öffnungswinkel des Strahls können wir den Laser-Lichtpunkt mit seinen rund 5 mm Durchmesser trotz der geringen Abstrahlleistung noch in einigen Metern Entfernung gut sehen. Dividiert man die Leistung durch die Lichtpunktfläche, erhält man eine Leistungsflussdichte der Strahlung von ca. 50 W/m².
Leuchtkraft und Leistungsaufnahme
Für die Charakterisierung der Leuchtkraft einer Lichtquelle ist es erforderlich, das gesamte Spektrum der von ihr emittierten sichtbaren Strahlung zu berücksichtigen. Nicht sichtbare Spektralanteile im Lichtstrom tragen nichts zur Leuchtkraft bei, erfordern gleichwohl Energie zu ihrer Erzeugung.
Ein Beispiel für eine besonders unwirtschaftliche Verwertung der Speise-energie ist die klassische Glühlampe. Sie verwandelt den Löwen-anteil (ca. 95 %) davon in Wärmestrahlung, also nicht sichtbares Licht, das einen Wärmeeindruck auf unserer Haut erzeugt. Nur ca. 5 % strahlt sie im Wellenlängenbereich des sichtbaren Lichts aus und regt damit die Rezeptoren in der Netzhaut des Auges an. Die Lichtausbeute als Quotient aus Lichtstrom v und eingesetzter elektrischer Leistung Pe beschreibt die Effizienz des Leuchtmittels (Gleichung 12).
Es ist also nicht sinnvoll, die aufgenommene Leistung eines Leuchtmittels in Watt (W) als Maß für seine Helligkeit heranzuziehen, sondern den von ihm abgegebenen Lichtstrom in Lumen (lm). Darin sind der Wirkungsgrad des Leuchtmittels und der visuelle Eindruck des menschlichen Beobachters berücksichtigt.
ANSI-Lumen
Zur objektiven Beschreibung des Lichtstroms einer Lampe für Projektoren wurde vom American National Standards Institute (ANSI) in der Norm IT7.227-1998 ein Verfahren angegeben, dessen Ergebnis den ANSI-Lumen-Wert des Leuchtmittels liefert. Die 2003 zurückgezogene Norm wird durch die Europanorm EN 61947-1,
Teil 1 in Zusammenhang mit der Norm IEC 61966-6 der International Electrotechnical Commission (IEC) und der DIN EN 61966, Teil 6 ersetzt. Dennoch hat sich der Begriff „ANSI-Lumen“ erhalten.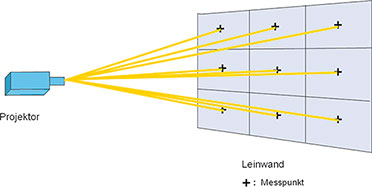
Bild 12: Das ANSI-Lumen beschreibt, wie hell ein Videoprojektor seine Bilder an die Wand wirft.
Das in der DIN 19045, Teil 8 genau beschriebene Verfahren teilt die Projektionsfläche in neun Felder ein, in deren Mitte die jeweilige Beleuchtungsstärke mit einem Lux-Meter gemessen wird (Bild 12).
Aus den neun Messwerten wird der Mittelwert gebildet. Dieser hängt von der Größe der Projektionsfläche ab. Den davon unabhängigen Lumen-Wert als gesamten vom Leuchtmittel ausgehenden Lichtstrom erhält man durch Multiplikation der Projektionsfläche mit dem Lux-Mittelwert. Der ANSI-Lumen-Wert hat den Vorteil, etwas über die tatsächlich an der Leinwand ankommende Lichtstrahlung auszusagen. So sind qualitätsmindernde Einflüsse von Projektoroptik, Lampe und Spiegel eliminiert. Natürlich gibt dieser ANSI-Lumen-Wert keine Auskunft über die Homogenität der Ausleuchtung des Projektionsfeldes.
Licht und Farbe
Farbsehen ist subjektiv
Über Auge und Gehirn eines Betrachters wird Licht zu einer Empfindung, die sowohl auf einem Helligkeits- als auch einem Farbeindruck beruht. Das menschliche Auge besitzt für das Farbsehen drei Arten von Lichtsensoren (Zäpfchen), deren Ausgangssignale (Farbreize) zum Gehirn geleitet und dort zu allen Farben verarbeitet werden. Das macht deutlich, dass das Farbempfinden keine absolut eindeutige Fähigkeit ist, sondern von Individuum zu Individuum variiert und von vielen weiteren Randbedingungen abhängt. Farbe ist also keine physikalische Größe, sondern eine Sinnesempfindung, an deren Entstehen physikalische, chemische, physiologische und psychologische Mechanismen mitwirken.
An Bild-1 wollen wir dies verdeutlichen. Hier sehen wir aus einer biologisch geprägten Sicht, wie es zu einem Farbeindruck beim menschlichen Beobachter kommt. Zunächst einmal bestrahlt eine Lichtquelle das betrachtete Objekt. Dieses absorbiert einen Teil des auftreffenden Lichtspektrums und reflektiert den Rest zum Auge des Betrachters. Bis jetzt hatten wir es mit rein physikalischen Vorgängen zu tun. Nun kommen Physiologie und Chemie ins Spiel, denn 3 Arten von lichtempfindlichen Rezeptoren in der Netzhaut des Auges werden durch den photometrischen Reiz stimuliert und erzeugen eine Erregung (excitation), die zur weiteren Verarbeitung über den Sehnerv an das Gehirn weitergeleitet wird. Die letztendliche Wahrnehmung der Farbe als Empfindung wird von der Psychologie (Prägungen, emotionale Begleitumstände ...) beeinflusst.
Farbmessung
In der DIN 5033 Blatt 1 wird definiert: „Die Ermittlung der drei eine Farbvalenz kennzeichnenden Maßzahlen (Farbmaßzahlen) heißt Farb-messung. Deshalb sind die Farbvalenzen Gegenstand der Farbmessung. Exakte (,valenzmetrische‘) Farbmessverfahren müssen die Farbvalenzen a) umkehrbar eindeutig, b) ohne Rücksicht auf die spektrale Beschaffenheit der Farbreizfunktion und c) gemäß dem Normalbeobachter bewerten. Das Ziel ist also eine zahlenmäßige Bestimmung einer Farbvalenz und nicht die einer Farbempfindung.“
Für die reproduzierbare Messbarkeit von Farben geht man wie in Bild-2 zusammengefasst vor. Am Wichtigsten dabei ist der Messempfänger. Er ermittelt die vom Objekt empfangenen Spektralfarben und übergibt sie zur Auswertung an einen Rechner, der daraus numerische Farbwerte bildet.
Bei der Farbmessung kommen im Wesentlichen zwei Verfahren zum Einsatz: das Dreibereichsverfahren und das Spektralverfahren (Bild-3).
Beim Dreibereichsverfahren empfangen drei entsprechend der Farbempfindlichkeit des Auges gefilterte Sensoren eines Colorimeters das vom Objekt reflektierte Licht und geben diese Messsignale an die Auswerteelektronik (Mikroprozessor). Dreibereichsfarbmessgeräte sind preiswert, portabel und einfach zu bedienen. Sie werden hauptsächlich zur Farbdifferenzmessung eingesetzt.
Beim Spektralverfahren wird das vom Objekt empfangene Licht von einem Spektrophotometer in die Wellenlängen des sichtbaren Spektrums aufgelöst und zur weiteren Auswertung bereitgestellt. Das Mess-ergebnis kann auch als Spektralkurve grafisch dargestellt werden, die beschreibt, wie stark das Objekt die einzelnen Spektralanteile reflektiert. Ein Spektrophotometer zeichnet sich durch hohe Messgenauigkeit und Vielseitigkeit, aber auch einen höheren Preis aus. Es ermöglicht komplexe farbmetrische Auswertungen und kann metamerische Effekte erfassen. Darunter versteht man das Phänomen, dass zwei Farben unter der einen Lichtquelle gleich, unter einer anderen voneinander abweichend erscheinen.
Das CIE-Farbmesssystem
Das menschliche Auge bewertet die Abstrahlung einer Lichtquelle oder eines reflektierenden Objekts mit den Normspektralwertfunktionen der drei Zäpfchenarten (Bild-4). Die Ermittlung der Normspektralfunktionen geht auf Messreihen der Commission Internationale de l‘Eclairage (CIE, Internationale Beleuchtungskommission) im Jahre 1931 zur Schaffung eines international gültigen Farbmetriksystems auf der Grundlage der Normfarbwerte Rot (R = 700,0 nm), Grün (G = 546,1 nm) und Blau (B = 435,8 nm) zurück. Eine statistisch relevante, normal farbsichtige Gruppe von Versuchspersonen musste dazu unter kontrollierten Verhältnissen Spektralfarben möglichst genau durch eine geeignete Mischung von Licht der drei CIE-Normfarbwerte R, G und B nachbilden. Dazu wurden ihnen die Farbproben in einem 2° großen Winkelsegment des Gesichtsfelds (entspricht einem Probendurchmesser von 1,75 cm bei einem Betrachtungsabstand von 50 cm, typisch für eine Lesesituation) vorgelegt, woraus der Name des Verfahrens CIE-1931-2° resultiert. 1964 wurde mit CIE-1964-10° für eine verbesserte Praxisnähe das Gesichtsfeld des Normalbeobachters auf 10° aufgeweitet. Die numerischen Unterschiede zwischen den Messreihen beider Verfahren sind gering.
Die von den Probanden gewählten Einstellwerte wurden gemittelt und interpoliert und führten zu den RGB-Spektralwertfunktionen in Bild-5. Die vom menschlichen Beobachter empfundene Farbe eines beleuchteten Objekts hängt davon ab, wie sich das von diesem reflektierte Licht auf die Normspektralwertfunktionen (auch als Augenempfindlichkeitskurven bezeichnet) verteilt.
Man erkennt, dass sich mit den drei RGB-Primärvalenzen der CIE-1931-2° nicht alle Spektralfarben durch additive Mischung erzeugen lassen. Für einige Spektralfarben müsste mindestens eine Spektralwertzahl negative Werte annehmen können. Damit alle reellen Farben durch rein additive Mischung darstellbar sind, kann man RGB-Spektralwertfunktionen r(λ), g(λ) und b(λ) mit einer Lineartransformation gemäß Gleichung 1 in Normspektralwertfunktionen x(λ), y(λ) und z(λ) überführen.
Eine Tabelle mit den exakten Werten der Normspektralwertfunktionen für den CIE-1931-2°- und den CIE-1964-10°-Beobachter findet man auf der Internetseite der CIE (http://files.cie.co.at/204.xls). Die Tabellenwerte für den 1931-2°-Beobachter wurden mit dem Tabellenkalkulationsprogramm OpenOffice Calc in die Kurven in Bild-4 umgesetzt.
Die Normspektralwertfunktionen beschreiben, wie die drei CIE-Normfarbwerte zu mischen sind, um eine bestimmte Spektralfarbe nachzubilden. So kommt z.-B. der durch eine Spektralfarbe mit einer Wellenlänge von 500-nm erzeugte Farbreiz aus der Überlagerung von x(500-nm)-+-
y(500-nm)-+-z(500-nm) zustande.
Es erstaunt, dass die gewählten Farbvalenzen aus drei festen monochromen Farben R,-G,-B farbgleich wie die nachzubildende beliebige Spektralfarbe empfunden werden. Aber darin zeigt sich, dass das Auge und die dahinter liegende „Signalverarbeitung“ (Gehirn) relativ leicht zu täuschen sind.
Als weiteren Beleg dafür betrachten wir Bild-6. Der darin gezeigte Effekt wird als Wasserfarben-Illusion bezeichnet. Der Name leitet sich ab aus der Empfindung des Betrachters, die Fläche zwischen den Farbkonturen sei wie mit einer leichten, gleichfarbigen aquarellartigen Füllung belegt. Die Farbmessungen 1 bis 4 belegen, dass dies nicht der Fall ist. Ein weiteres Beispiel, das verdeutlicht, dass die Wahrnehmung einer Farbe keinesfalls objektiv ist, zeigt Bild-7. Bei eingehender Betrachtung scheint der rechte rote Ring vor blauem Hintergrund „leuchtender“ als der linke in gelbem Umfeld. Dies ist ein kontrastabhängiger subjektiver Effekt, denn die Ringfarben sind identisch.
Mit den Spektralfunktionen aus Gleichung-1 werden 2°-Normfarbwerte X, Y und Z gemäß Gleichung-2 gebildet. Sie können für Blickwinkel bis 4° eingesetzt werden und sind nicht für leuchtende Flächen (Körperfarben) anwendbar. Der Normfarbwert Y hängt von der Normspektralwertfunktion y(λ) ab, die der Hellempfindlichkeit des Auges entspricht. Daher ist Y ein Maß für die Helligkeit einer Farbe. Die Normierungskonstante K ist so gewählt, dass für einen vollkommen mattweißen (d.-h. ideal streuenden) Körper bei jeder Lichtart stets Y = 100 wird.
Die CIE-1931-2° zugrunde liegenden Normfarbwertzahlen X, Y, Z werden auf das Intervall [0..1] normiert Die CIE-1931-2° zugrunde liegenden Normfarbwertzahlen X, Y, Z werden auf das Intervall [0...1] normiert und man erhält die CIE-Normfarbwertanteile x, y und z (Gleichung 3).
Wegen x + y + z = 1, genügt es, zwei CIE-Normfarbwert-anteile anzugeben, um die Zusammensetzung jeder Farbe auszudrücken.
CIE-Norm-Farbdiagramm
Trägt man die x- und y-Farbkoordinaten aller sichtbaren Spektralfarben rechtwinklig gegeneinander auf, entsteht eine gekrümmte, offene Kurve. Durch die Verbindung zwischen Rot und Purpur (Purpurgerade) wird sie geschlossen. Die umfasste Fläche („Schuhsohle“) heißt CIE-Normfarbtafel (Bild-8). Sie enthält die Farb-orte aller reellen Farben. Bei x = y = z = 0,33 liefern alle drei Rezeptorarten des Auges den gleichen Reiz, was als Lichtfarbe Weiß empfunden wird (Unbuntpunkt, Weißpunkt). Mit der ergänzenden Angabe von Y entsteht das Wertetripel x, y, Y, das sowohl Farbe (Chromazität: x, y) als auch deren Helligkeit (Luminanz: Y) beschreibt.
Ohne auf alle Details der CIE-„Schuhsohle“ einzugehen, wollen wir ihre wichtigsten Eigenschaften kurz streifen. Auf der äußeren umlaufenden Kontur (Spektralfarbenzug) wird der reine spektrale Farbton in höchster Sättigung von 380-nm (Purpur) bis 780-nm (Rot) abgebildet, in Richtung zum Weißpunkt nimmt seine Sättigung bis auf null ab. Unter Sättigung können wir also den Unterscheidungsgrad des farbigen Reizes von einem achromatischen (farblosen) Reiz verstehen.
Nun ist es aber so, dass der Weißpunkt bei Licht, welches von der spektralen Zusammensetzung des Tageslichts abweicht, seine Lage in der CIE-„Schuhsohle“ verändert. Unter Glühlampenlicht (Normlichtart-A) sehen ein Weiß und alle anderen Farben eben anders aus als an einem Nordfenster bei bedecktem Himmel (Normlichtart D65, mittleres Tageslicht). Deshalb wird man in guten Modehäusern mit der Textilie, für die man sich interessiert, auch an ein nördliches Tageslichtfenster geführt, um einen „objektiven“ Eindruck von deren Farbwirkung zu erhalten. Um bei der Farbbewertung vom Tageslicht unabhängig zu sein, wurden künstliche Lichtquellen mit reproduzierbaren Eigenschaften entwickelt (Normlichtquellen).
Für die Charakterisierung des von einem Leuchtmittel abgegebenen Lichts als „kalt“ oder „warm“ ist die beleuchtungsabhängige Lage des Weißpunkts ausschlaggebend. Die Linie aller Weißpunkte ergibt sich aus der Farbe eines Schwarzen Körpers (black body) bei verschiedenen Farbtemperaturen von roten über gelbe zu blauen Farborten und heißt deshalb auch „Black-Body-Kurve“.
Schwarzer Strahler
Unter einem Schwarzen Körper (Schwarzer Strahler) versteht man die Idealisierung eines Gebildes (Kohlenstoff in seiner graphitischen Form kommt bis auf drei Prozent an das Ideal heran), das auftreffende elektromagnetische Strahlung, unabhängig von deren spektraler Zusammensetzung (also auch Licht) vollständig verschluckt. Somit ist ein Schwarzer Körper auch völlig undurchlässig und ohne jegliche Reflexion (Spiegeln, Streuen), eben ein perfekter Absorber. Die absorbierte Strahlungsenergie führt zu einer Erhöhung seiner thermischen Energie (Körperwärme), die er vollständig als Strahlung abgibt.
Eine Realisierung, die einem idealen Strahler bereits recht nahe kommt, ist ein auf der Innenseite berußter Kasten mit einer kleinen Eintrittsöffnung für die Strahlung (Licht), wie ihn Bild-9 zeigt. Parallel und schräg zu den Seitenwänden einfallende Lichtstrahlen werden mehrfach an den Innenwänden jeweils unter Absorption eines Teils ihrer Energie reflektiert und finden nicht mehr heraus. Mit anderen Worten: Der Kasten hat sie verschluckt, wie es ein Schwarzer Strahler tun soll.
Intensität und spektrale Verteilung der Abstrahlung war erst durch das von Max Planck um 1900 empirisch aufgestellte Strahlungsgesetz berechenbar. Darin ging Planck davon aus, dass elektromagnetische Strahlung nicht kontinuierlich, sondern „portionsweise“ in Quanten abgegeben oder aufgenommen wird. Diese Hypothese war die Geburtsstunde der Quantenmechanik und erlöste die Physiker von einer quälenden Frage. Nach dem Strahlungsgesetz von Rayleigh-Jeans nämlich, welches das Strahlungsverhalten eines Schwarzen Körpers bei niedrigen Frequenzen sehr gut beschreibt, aber mit steigender Frequenz zunehmend überzeichnet, müsste ein Schwarzer Körper, über alle Frequenzen integriert, eine unendlich große Energie abstrahlen („Ultraviolettkatastrophe“). Die von Planck errechnete Strahlungsverteilung eines idealen
Schwarzen Strahlers bei verschiedenen Temperaturen (Kelvin:-K) zeigt Bild-10.
Man erkennt, dass die Intensität der Strahlung mit steigender Temperatur zunimmt und sich ihr spektrales Maximum in Richtung kürzerer Wellenlängen (höhere Frequenzen) verschiebt. Auf jeden Fall deckt sich ein Teil der Spektren mit dem Spektralbereich des sichtbaren Lichts und das Maximum des Strahlerspektrums liegt nur zwischen Strahlertemperaturen von 5000-K bis etwa 7500-K im sichtbaren Bereich. Mit ansteigendem Maximum des Strahlungsspektrums eines Schwarzen Strahlers steigt seine Energie und umgekehrt. Bei 7500-K verlässt das spektrale Maximum den Bereich des sichtbaren Lichts und geht ins Ultraviolette. Unter 5000-K wandert das Maximum ins Infrarote.
Das Maximum des Spektrums eines Schwarzen Strahlers ergibt sich entsprechend dem Wien’schen Verschiebungsgesetz zu λmax = (0,002898 K)/T. Setzen wir z.-B. T = 9000-K ein, ergibt sich λmax = 322-nm, was gut mit Bild-10 übereinstimmt.
Auf der Homepage von Matthias Borchardt (www.mabo-physik.de/plancksche_strahlungskurve.html) steht ein Programm (planck.exe) zum Download, das die Intensitätskurven der Strahlung als Funktion der Strahlertemperatur grafisch ausgibt.
Fazit: Als Farbtemperatur bezeichnet man diejenige Temperatur, die ein Schwarzer Körper haben müsste, damit dessen Licht einen möglichst ähnlichen Farb-eindruck hervorruft wie die tatsächlich vorhandene Beleuchtung. „Warmes“ Licht ist demnach langwelliger als „kaltes“ Licht.
Richtwerte für einige Lichtquellentypen gibt die Tabelle in Bild-11.
In engem Zusammenhang mit der Farbsättigung stehen die Begriffe Farbigkeit oder Farbintensität als wahrgenommene „Buntheit“. Jeder kann aus persönlicher Anschauung nachvollziehen, dass die Beleuchtung von Farbflächen auf die Farbstärke Einfluss hat. Helle Beleuchtung führt zu einem intensiveren Farb-eindruck als dunklere Beleuchtung. Im Extremfall, bei ganz schwachem Licht, ist gar kein Buntsehen mehr möglich, weil das Sehen von den empfindlicheren Schwarz-Weiß-Stäbchen in der Netzhaut anstelle der drei Arten von Farb-Zäpfchen übernommen wird. Das Sprichwort „Nachts sind alle Katzen grau“ veranschaulicht dies.
Neben Farbton und Sättigung einer Farbe empfindet der Mensch deren Helligkeit als die dritte ihrer grundlegenden Eigenschaften. Der stärkste Unterschied besteht zwischen Schwarz und Weiß und bei den bunten Farben zwischen Violett und Gelb. Auf die Unterscheidung zwischen farbmetrischer und fotometrischer Helligkeit wollen wir an dieser Stelle nicht weiter eingehen. Es müssten dazu der Begriff „Vergleichsfarbe“ und das Weber-Fechner-Gesetz näher erläutert werden. Letzteres beschreibt den logarithmischen Zusammenhang zwischen wahrgenommener und gemessener Lichtintensität.
Es gibt neben dem CIE-System eine Vielzahl weiterer Farbmesssysteme, die hier aus Platzgründe nicht angesprochen werden können.
Farbwiedergabeindex als Maß für die Beleuchtungsqualität
Als wichtiges Maß für die Fähigkeit des von einer bestimmten Beleuchtungsquelle ausgesandten Lichts, die Farben unterschiedlicher bestrahlter Objekte möglichst naturgetreu wiederzugeben, gilt der Farbwiedergabeindex CRI (Color Rendering Index). Er wurde von der CIE sinngemäß wie folgt definiert: „CRI: Wirkung eines Leuchtmittels auf die Farbanmutung von Objekten durch bewussten oder unbewussten Vergleich mit der Farbanmutung unter einer Referenzbeleuchtung.“
Als Referenz dient bis zu einer Farbtemperatur von 5000-K das Licht eines Schwarzen Strahlers mit der entsprechenden Farbtemperatur. Darüber hinaus bildet eine tageslichtähnliche Lichtquelle den Bezug (Quelle: Wikipedia). Der CRI beschreibt mit einem Wert zwischen 0 und 100 den Unterschied zwischen Ist- und Normbeleuchtung in Bezug auf die Farbwiedergabe und ist damit ein Maß für die Farbwiedergabetreue unter der zu beurteilenden Ist-Beleuchtung.
Ein Beispiel ohne wissenschaftlichen Anspruch entstand am Schreibtisch des Autors. Es zeigt einen Tesafilmabroller unter dem Licht einer energiesparenden Schreibtischlampe mit der Lichttemperaturangabe 2700-K und einer Taschenlampe mit 9 im blau-weißen Bereich Licht emittierenden Dioden (Bild-12). Man erkennt deutlich, dass das mit stärkeren Rotanteilen ausgestattete Schreibtischlampenlicht zu einem intensiveren Rot und einer schwächeren Wahrnehmung des Blauanteils im Bild führt, wogegen die blaustichige Taschenlampe das Blau deutlich hervorhebt und das Rot im Bild zurücknimmt.
CRI-Messverfahren
In der DIN-6169 sind 14-Testfarben, von denen die ersten 8 nur schwach gesättigt sind, mit einem genormten Remissionsverlauf (Remission ist im Gegensatz zu spiegelnder Reflexion das diffuse Rückstrahlen, lateinisch: remittere = zurückschicken) definiert (Bild-13). Für jede dieser Farben kann nun ein spezifischer Farbwiedergabeindex R1...R14 berechnet werden. Wie dabei vorzugehen ist, beschreibt die CIE-Publikation 13.3-1995.1 „Method of Measuring and Specifying Color Rendering Properties of Light Source (1995)“. Die Berechnung des CRI ist nicht ganz einfach. Der Ablauf ist z.-B. in dem Dokument www.lrc.rpi.edu/programs/solidstate/assist/pdf/AR-SpecifyColorRec-March2010.pdf auf den Seiten 12-bis-17 ausführlich dargestellt.
Ein zusammenfassender Wert ist der allgemeine Farbwiedergabeindex-Ra, der als arithmetischer Mittelwert den Durchschnitt aus den Farbwiedergabeindizes R1 bis R8 bildet (Gleichung-4). Er wird meist mit CRI gleichgesetzt.
Eine Übersicht der mit bestimmten Lichtquellen erreichbaren Farbwiedergabeindizes gibt die Tabelle in Bild-14. Beim Licht einer 60-W-Glühlampe mit einer Farbtemperatur von etwa 2700-K ergibt sich ein allgemeiner Farbwiedergabeindex von 100, die Farbwiedergabe ist also optimal. Überhaupt keine Farb-unterscheidung erlaubt eine Beleuchtung durch eine monochrome Lichtquelle wie eine Natrium-Niederdrucklampe. Dementsprechend kann der Farbwiedergabe-index sogar negative Werte annehmen.
Problematisch sind Farben mit einer ungleichmäßigen spektralen Intensitätsverteilung. So liegt der CRI heutiger im Markt erhältlicher weißer Leuchtdioden (LED: Light Emitting Diode) bei 70. Ihr Licht wird von einem blauen InGaN-Chip (Indium-Gallium-Nitrid) erzeugt, der mit gelbem Phosphor ummantelt ist, der einen Teil des blauen Lichts in gelbes umwandelt. Die Mischung aus blauem und gelbem Licht wird vom menschlichen Auge als kühles Weiß wahrgenommen. Wegen des schwachen Rotanteils kann mit kaltweißen LEDs nur ein CRI von etwa 70 erreicht werden.
Ein Rotanteil kann auf zwei Arten erhöht werden:
1. Hinzufügen von rotleuchtendem Phosphor in die LED-Umhüllung. Der Vorteil dieser Lösung besteht in der unveränderten Ansteuerung, nachteilig ist eine Reduzierung der Leuchtkraft um typ. 10 %.
2. Ergänzung der kaltweißen LED durch eine oder mehrere benachbarte rotleuchtende LEDs. Vorteil: Die Mischfarbe enthält dann einen erhöhten Rotanteil im Spektrum (Bild-15). Dieser ist durch die Ansteuerung der Dioden in gewissen Grenzen variabel. Nachteil: erhöhter Aufwand an Dioden und Ansteuerungselektronik.
Lichtquellen, die auf der Entladung von Leuchtgasen beruhen, haben im Gegensatz zu Leuchtstofflampen ein ausgeprägtes Linienspektrum und daher einen weniger hohen Farbwiedergabeindex (Bild-16).
Kritik am CRI
Der Farbwiedergabeindex ist kein eindeutiges Maß für die Farbtreue. Ein hoher CRI bedeutet keinesfalls immer, dass alle Farben gut wiedergegeben werden. Tatsächlich können Lichtquellen mit signifikant anderer spektraler Zusammensetzung als die Referenzquelle den gleichen CRI aufweisen, obwohl sie eine stark abweichende Farbwirkung des bestrahlten Objekts hervorrufen.
Das CIE und verschiedene andere Organisationen arbeiten an einem eindeutigeren Maß für die Charakterisierung der Farbwiedergabe von Lichtquellen. Bis dahin ist der CRI die allgemein akzeptierte Beschreibungsgröße für die Farbqualität einer Lichtquelle oder Beleuchtung.
Zusammenfassung
Einfluss auf den Farbeindruck haben eine Vielzahl von messbaren und subjektiven Einflussgrößen: spektrale Reflexionseigenschaften des Sehobjekts, spektrale Verteilung (Farbton) der Beleuchtung und ihre Intensität (Helligkeit), Stimmungen, Umfeld und manches mehr.
Mit freundlicher Genehmigung von ELV www.elv.de
Exkurs: Lichtspektren verschiedener Displaytechnologien
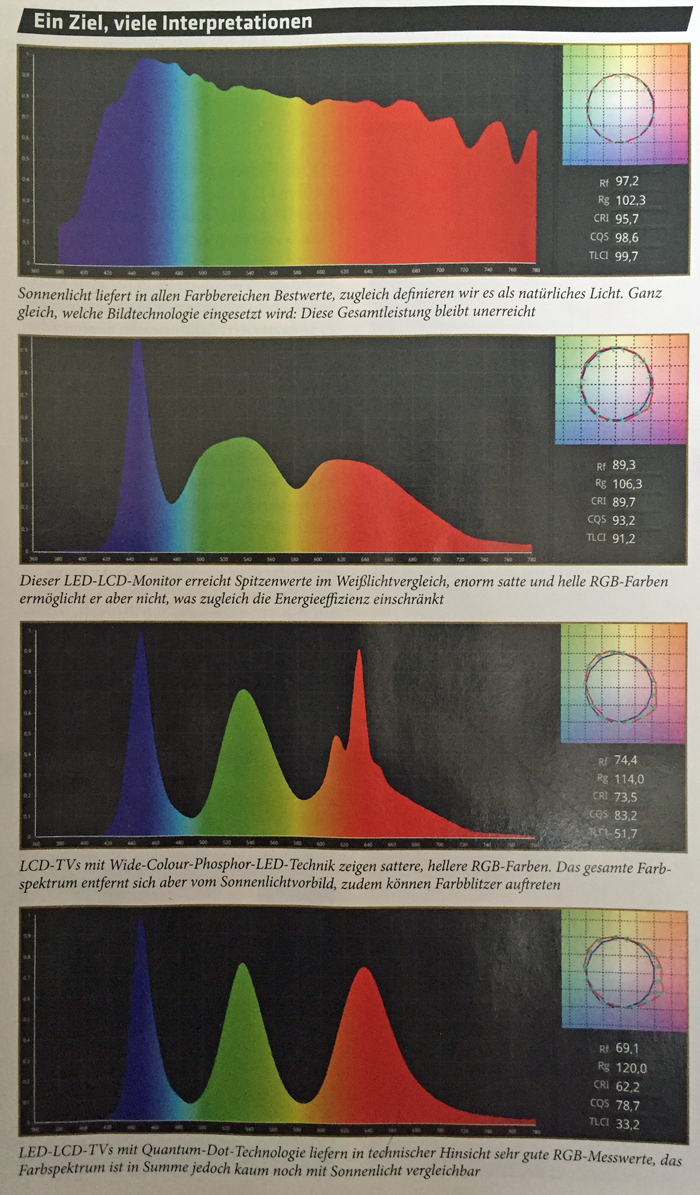 Quelle: HDTV Magazin 5/2016 - S. 37
Quelle: HDTV Magazin 5/2016 - S. 37
