JPEG ist die allgemein gebräuchliche Bezeichnung eines digitalen Bildformats, welches im Jahre 1992 normiert wurde. Die Abkürzung steht für 'Joint Pictures Expert Group' und bezeichnet das Gremium, welches für die Normierung des Bildstandards zuständig war.
In den fast 20 Jahren seit seiner Normierung hat sich das JPEG-Format zum bekanntesten und am weitesten verbreiteten Format zur Speicherung digitaler Bilder entwickelt. Der Bekanntheitsgrad von JPEG ist hoch, seine genaue Funktionsweise jedoch nur wenigen bekannt. Dieser Bericht soll auch dem Laien ein Bild über die Nutzung und die internen Vorgänge des Formats vermitteln.
Um alle Aspekte zu beleuchten ist der Bericht in zwei Teile unterteilt. Teil 1 befasst sich mit der Theorie rund um das Verfahren, Teil 2 mit den praktischen Aspekten. Den zweiten Teil dieses Berichts finden Sie auf den Seiten der Firma Burosch unter www.burosch.de.
Über diesen Link bekommen Sie eine PDF mit allen Bildern in hoher Auslösung.
JPEG in der Praxis
Geschätzte 80% aller Bilddaten im Internet liegen im JPEG-Format vor, die übrigen 20% als PNG, und seltener auch im GIF, BMP und SVG Format. Jeder gängige Internetbrowser, jedes Bildbetrachtungs- und Bildbearbeitungsformat versteht das Format, kann es anzeigen, bearbeiten oder speichern. Außer Computern sind mittlerweile auch viele anderen Geräte der Unterhaltungselektronik, etwa externe und integrierte Abspielgeräte für TVs, Mobiltelefone und Spielkonsolen, in der Lage das Format anzuzeigen. In geringen Abwandlungen kommt JPEG auch als Bewegtbildformat ('Motion JPEG', 'MJPEG') und als Format zur Speicherung dreidimensionaler Bilder (z.B. als 'JPEG Stereo', 'JPS' oder 'Multi Picture Object', 'MPO') zum Einsatz.
Digitale Photographie
In der digitalen Photographie ist JPEG das typische Ausgabeformat. Man könnte sagen, dass insbesondere die moderne Digitalkamera dem JPEG-Format zu seinem Siegeszug verholfen hat, jedoch wäre dies nur ein Teil der Wahrheit, denn erst das JPEG-Format hat die Digitalkamera in ihrer heutigen Form ermöglicht. Erst die niedrige Komplexität und die hohe Kompression des JPEG-Formats machte es möglich, ab etwa Mitte der Neunziger Jahre des vorigen Jahrhunderts, bei immer noch hohen Kosten für Mikroprozessoren und Speicher massenmarkttaugliche Digitalkameras zu produzieren.
Durch die weite Verbreitung der Digitalkamera werden private Photographien heute üblicherweise im JPEG-Format aufbewahrt, gespeichert auf Speicherkarten, Festplatten, USB-Sticks, CD- und DVD-ROMs. Die noch vor einigen Jahren übliche Aufbewahrung als Lichtbild, Dia oder Negativ gehört der Vergangenheit an.
Heimische Abspielgeräte
Mit der zunehmenden Verbreitung von JPEG-Bildern auf heimischen Datenträgern mussten auch die analogen Abspielgeräte der Vergangenheit aus den Haushalten weichen. Praktisch jedes digitale Gerät, welches über ein geeignetes Display verfügt, kann heute JPEGs anzeigen, sei es Mobiltelephon, portable Spielkonsole, Tablet-PC, TV oder gar MP3-Player. Externe Abspielgeräte wie Video-CD-, Video-DVD- oder Blu-ray Player können schon seit Anbeginn außer Bewegtbildern im MPEG-Format zumindest auch statische Bilder im JPEG-Format anzeigen.
Insbesondere HD-fähige TVs bieten heute große Bilddiagonalen und ein Vielfaches der Auflösung früherer Geräte. Sie ermöglichen brillante Wiedergabe von Photographien direkt im heimischen Wohnzimmer. Üblicherweise verfügen diese Geräte auch über einen integrierten Medienplayer und einen USB-Anschluss zum Einspeisen von Bildmaterial. War es früher üblich, Bekannten Photographien als Dias auf dem Diaprojektor vorzuführen, wofür ein wenig portabler Diaprojektor sowie sperriges Bildmaterial notwendig war, so wird diese Aufgabe heute vollständig vom heimischen TV übernommen und es genügt ein einziger USB Stick oder eine Speicherkarte zum Transport vieler tausender Bilder.

Abbildung 1: Darstellung einer Photographie im JPEG-Format auf einem modernen, HD-fähigen LCD Fernseher.
(Bild bereitgestelllt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Zukunft des Formates
Mit dem Einzug von 3D-fähigen TVs in die Wohnzimmer gewinnt auch die dreidimensionale Photographie an Bedeutung und erste an den Massenmarkt gerichtete Geräte zur Aufnahme stereoskopischer Bilder sind bereits verfügbar. Viele dieser Geräte nutzen das MPO Format, welches mehrere Bilder im JPEG-Format gemeinsam mit Informationen zum jeweiligen Blickwinkel in einer einzigen Datei speichert. Außer typischer stereoskopischer Bilder (bestehend aus zwei Bildern, jeweils aus dem Blickwinkel des linken und rechten Auges) sind in dem Format auch dreidimensionale Panorama-Ansichten, bestehend aus beliebig vielen Bildern einer Szene, möglich.
Warum JPEG?
JPEG ist das weltweit am meisten genutzte Format zur Speicherung digitaler Bilder. Worin liegt das Erfolgsgeheimnis des Formates, und warum wird ein beinahe 20 Jahre alter Standard in der schnelllebigen Digitaltechnik weiterhin so flächendeckend eingesetzt?
Hohe Kompression
Der Haupteinsatzgrund für das JPEG-Format liegt in seiner hohen Kompression im Vergleich zu anderen Formaten. Die hohe Kompression hat ihre Ursache darin, das JPEG verlustbehaftete, für die menschliche Wahrnehmung optimierte Techniken zur Einsparung von Datenvolumen nutzt. Das Ein- und Ausgabebild im JPEG Verfahren ist so zwar nicht identisch, jedoch für den menschlichen Betrachter so ähnlich, das ein Unterschied nicht oder kaum erkennbar ist. Andere Formate, wie z.B. das PNG Format nutzen nur verlustfreie Kompressionstechniken und erreichen nicht annähernd die Kompressionsrate, welche JPEG bietet.
Ein einfaches Beispiel soll diesen immensen Vorteil verdeutlichen: Eine gängige Speicherkarte, wie sie in Digitalkameras zum Einsatz kommt, hat eine Größe von etwa 2GB. Würde man diese Karte mit unkomprimierten Farbbildern der Auflösung 1920x1080 Pixel füllen, so fänden etwa 322 Bilder Platz auf der Karte - dies ist nicht wenig, gemessen am typischen Bildaufkommen eines Hobbyphotographen jedoch auch nicht viel. Würde man die Bilder stattdessen im PNG Format speichern, so würde der Platz für etwa die doppelte Menge an Bildern, 644, genügen. Im JPEG-Format passt, ohne dass der Verlust an Qualität für den menschlichen Betrachter ersichtlich ist, gut die die vierfache Menge, 1288 Bilder, auf die Karte.
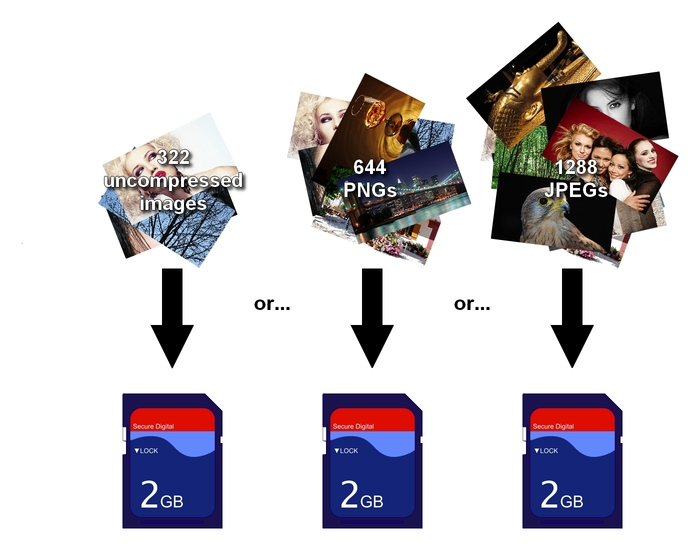
Abbildung 2: Raum für mehr Bilder auf der Speicherkarte durch das JPEG Verfahren.
(Bilder bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Niedrige Komplexität
Zumindest aus der Sichtweise eines Prozessors ist JPEG ein Verfahren niedriger Komplexität. Trotz der hohen Kompression sind nur wenige CPU-Zyklen auf dem Weg vom unkomprimierten Bild zum JPEG Format notwendig. Die Komplexität des Verfahrens ist so gering, dass heute auch günstigste Mikroprozessoren, wie sie etwa in Mobiltelefonen verwendet werden, in der Lage sind, JPEG Bilder in Echtzeit zu schreiben und/oder anzuzeigen.
Alternativen zu JPEG
Seit 1992 wurden verschiedene andere, dem JPEG Format technisch überlegen Formate entwickelt, welche stärkere Kompression bei besserer Darstellungsqualität, höhere Farbtreue oder bessere Möglichkeiten zur Speicherung von Metadaten bieten. Unter anderem zählen hierzu die vom selben Gremium standardisierten Bild-Formate JPEG-2000 und JPEG-XR. Keines dieser Formate konnte sich letztendlich beim Endnutzer durchsetzen, was nicht zuletzt an der durch die genannten Vorteile bereits sehr hohen Verbreitung und Akzeptanz des JPEG-Formats zum Zeitpunkt der Veröffentlichung lag.
JPEG – ein perzeptuelles Kompressionsverfahren
JPEG nutzt, wie viele anderen erfolgreichen komprimierten Medienformate (unter anderem auch MP3 und MPEG-1/-2/-4) ein perzeptuelles Kompressionsverfahren. Bei seiner Entwicklung flossen Erkenntnisse der Psychophysik ein, um durch Wegnahme von – für den Menschen – irrelevanter Information große Einsparungen am Datenvolumen zu ermöglichen. Im Rahmen der Entwicklung des Verfahrens wurden die eingesetzten Techniken an einer Vielzahl von Versuchspersonen getestet, um so bestmögliche Resultate für den durchschnittlichen Konsumenten zu garantieren.
Der Weg von den unkomprimierten Bildrohdaten zur komprimierten JPEG-Datei lässt sich grob in folgende sechs Schritte zerlegen:
- Extraktion der Rot-, Grün- und Blau-Anteile aus den Bildrohdaten
- Farbraumkonversion in den YCbCr Farbraum und Farbunterabtastung
- Überführung der Farbanteile aus dem Ortsbereich in den Frequenzbereich
- Anpassung von Qualität und Dateigröße durch Quantisierung
- Intelligente Reorganisation der Daten
- Kodierte Speicherung der Daten
Bildrohdaten - das Ausgangsmaterial
Der übliche Erzeuger einer JPEG-Datei ist eine Digitalkamera. Die Funktionsweise einer Digitalkamera unterscheidet sich nur gering von der traditioneller analoger Kameras – ein Objektiv bündelt das einfallende Licht, ein Verschluss steuert die Belichtungszeit und ein Aufnahmemedium fängt das Bild ein. Im Falle der Digitalkamera ist das Aufnahmemedium ein Photosensor. Seine Aufgabe ist es, das aufgefangene Licht in ein digitales Signal umzuwandeln, welches dann wiederum als Bildrohdaten in der Kamera zwischengespeichert wird.
In den meisten Digitalkameras kommt als Photosensor ein Bayer-Sensor zum Einsatz. Dieser besteht aus einer Schicht von Photozellen, welche mit einem schachbrettartigen Farbfilter überzogen ist. Jede Photozelle arbeitet gleich und kann nur Helligkeitswerte erfassen. Im Farbfilter wechseln sich Rot-, Grün- und Blaufilter ab, jeweils 25% des Farbfilters bestehen aus Rot- und Blau-Anteilen, die restlichen 50% aus Grünfiltern (siehe Abbildungen 3 und 4).
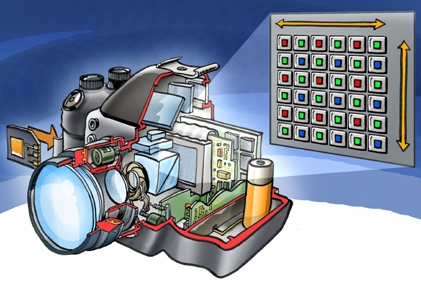
Abbildung 3: Bayer-Sensor innerhalb einer typischen digitalen Spiegelreflexkamera.
(Grafik erstellt von Peter Welleman, Lizenz: creativecommons.org/licenses/by/2.5/deed.de)
Die Aufteilung der Farben im Filter beruht auf der Tatsache, dass das menschliche Auge auf die Farbe Grün empfindlicher reagiert als auf die Farben Rot und Blau. Die Wellenlänge des grünen Lichts liegt zwischen der des roten und blauen Lichts, grünes Licht stellt daher eine gute Repräsentation für die Grundhelligkeit eines Bildes dar. Durch die Anordnung des Farbfilters im Bayer-Farbfilter ergibt sich folgende Komplikation: Nur 50% der Pixel des Grünanteils und nur 25% der Pixel des Rot- und Blau-Anteils werden vom Bayer-Sensor bereitgestellt. Alle übrigen Pixel müssen durch Interpolation errechnet werden. Durch Unzulänglichkeiten des menschlichen visuellen Systems, die generelle Ähnlichkeit benachbarter Pixel und geschickte Algorithmen zur Interpolation fällt dies dem ungeschulten Auge jedoch kaum auf.

Abbildung 4: Ein typischer Bayer-Filter. (Quelle: Wikimedia Commons)
Weniger verbreitet als der Bayer-Sensor ist der Super-CCD-Sensor. Dieser nutzt ein ähnliches Prinzip, eine Schicht von Photozellen und einen darüber liegenden Farbfilter, ordnet die Photozellen und den Farbfilter jedoch in einem aus Sechsecken bestehenden Wabenmuster an. Auf diese Weise sind die vertikalen, horizontalen und diagonalen Abstände zwischen den erfassten Helligkeitswerten geringer, und es kann mit höherer Qualität interpoliert werden. Ein völlig anderes Prinzip nutzt der Foveon X3 Sensor: Er nutzt statt nur einer Schicht von Photozellen drei – eine für jede der drei Grundfarben. Eine Interpolation ist so nicht notwendig, und es kann - anders als bei Bayer- und Super-CCD-Sensoren - für alle Farbkomponenten die gleiche, hohe örtliche Auflösung erreicht werden.
Erzeuger einer JPEG-Datei kann auch ein Bildbearbeitungsprogramm sein – man denke an einen Screenshot oder an ein bearbeitetes und nochmals gespeichertes Photo. Die genannten Komplikationen treten in diesem Fall jedoch nicht auf, da Bildbearbeitungsprogramme intern ohnehin mit Rot-, Grün- und Blau-Anteilen rechnen.
Farbraumkonversion und Farbunterabtastung
Der ansonsten sehr gebräuchliche, auf den Farben Rot, Grün und Blau basierende RGB Farbraum birgt für die perzeptuelle Kompression ein grundsätzliches Problem: Zwischen den einzelnen Farbanteilen bestehen große statistische Abhängigkeiten und viele Information ist unnötig oft vorhanden. Diese Tatsache ist leicht ersichtlich, wenn man ein herkömmliches Photo in seine Rot-, Grün- und Blau-Anteile zerlegt und sich diese betrachtet. Aus jedem einzelnen der Anteile lässt sich das ursprüngliche Bild nicht nur erahnen, es ist praktisch jedes Detail erkennbar (siehe Abbildung 5). Abhilfe gegen diesen Umstand schafft JPEG durch eine Farbraumkonversion in den YCbCr Farbraum. Dieser stellt das Bild dar durch einen Luminanzanteil (Y), welcher die Grundhelligkeit des Bildes, einem Chrominanzanteil (Cb), welcher die Abweichung in Richtung Blau und einem Chrominanzanteil (Cr), welcher die Abweichung in Richtung Rot repräsentiert.
Die Luminanz- (Y) und die Chrominanz-Anteile (Cb und Cr) können, Pixel für Pixel durch diese Formel aus den Rot- (R), Grün- (G) und Blau-Anteilen (B) errechnet werden:
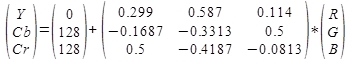
Umgekehrt können RGB-Anteile aus YcbCr-Anteilen wie folgt berechnet werden:
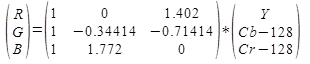

Abbildung 5: Realbild und seine Trennung in die Farbkomponenten Rot, Grün und Blau.
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)

Abbildung 6: Realbild und seine Trennung in Luminanz (Y) und Chrominanzen (Cb und Cr).
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Während im RGB Farbraum der Informationsgehalt eines Bildes über drei Farbanteile annähernd gleichverteilt ist, ist im YCbCr Farbraum ein Großteil des Informationsgehalts im Luminanzanteil konzentriert. Dieser Umstand für sich genommen bringt noch keine Einsparungen, der Vorteil der Farbraumkonversion besteht im größeren Potential zur Irrelevanzreduktion. Das menschliche Auge kann feine örtliche Farbunterschiede in natürlichen Bildern nur schwer wahrnehmen (dies fällt bereits bei Betrachtung von Abbildung 6 auf), daher kann man die Auflösung der Chrominanzanteile verringern, ohne dass es auffallen würde. Bei der Dekompression müssen die Farbanteile durch Interpolation wieder auf ihre ursprünglich Größe gestreckt werden.
Der Vorgang des Verringerns der Chrominanzenauflösungen wird auch Farbunterabtastung genannt. In der Praxis genutzte Arten der Farbunterabtastung sind die 4:2:0 Unterabtastung, bei der Cb und Cr vertikal und horizontal auf jeweils die Hälfte der ursprünglichen Größe reduziert werden (siehe Abbildung 7), und die 4:2:2 Unterabtastung, bei der Cb und Cr nur horizontal auf die Hälfte ihrer ursprünglichen Größe reduziert werden (siehe Abbildung 8). Eine weitere Form der Farbunterabtastung, die 4:4:4 Unterabtastung, ist eigentlich gar keine Farbunterabtastung, da sie die Chrominanzanteile bei ihrer ursprünglichen Auflösung belässt und keine Änderungen vornimmt.

Abbildung 7: Veranschaulichung der 4:2:0 Farbunterabtastung.
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)

Abbildung 8: Veranschaulichung der 4:2:2 Farbunterabtastung.
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Die häufigste Art der Farbunterabtastung im JPEG-Format bei durch Digitalkameras erzeugten Bildern ist die 4:2:2 Unterabtastung. Der Grund liegt einerseits in den ohnehin vorhandenen Unzulänglichkeiten der Bayer- und Super-CCD-Sensoren bei der Wiedergabe von Farbe, andererseits darin, dass diese Farbunterabtastung einen guten Kompromiss zwischen Einsparungen und kaum merklichen Qualitätsverschlechterungen darstellt. Nur bei nachbearbeiteten Bildern und wenn die örtliche Farbauflösung eines Foveon X3 Sensors genutzt werden soll, kann der Verzicht auf, bzw. die 4:4:4 Farbunterabtastung Sinn machen.
Die Auswirkungen der 4:2:2 und 4:2:0 Unterabtastungen auf die visuelle Qualität sind allgemein gering bzw. kaum vorhanden. Sie können nur durch spezielle, künstliche Testbilder und entsprechende Vergrößerung für den menschlichen Betrachter sichtbar gemacht werden (siehe Abbildung 9).
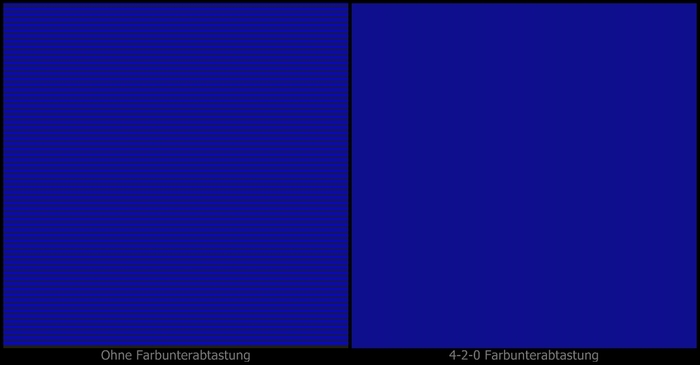
Abbildung 9: Auswirkungen der Farbunterabtastung durch Vergrößerung sichtbar gemacht -
im Testbild wechseln sich vertikal verschiedenfarbige Zeilen der Größe 1 Pixel ab.
(Testbild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Andere Farbunterabtastungen als 4:2:0, 4:2:2 und 4:4:4 werden in der Praxis nicht genutzt, sind aber theoretisch im JPEG-Format möglich. Denkbar, aber nicht sinnvoll wäre z.B. eine Unterabtastung, die die Chrominanzanteile nur horizontal auf ein Viertel der ursprünglichen Größe reduziert, oder auch eine, die die Chrominanzanteile vertikal auf ein Drittel und horizontal auf die Hälfte reduziert. Als einzige Einschränkung für die Farbunterabtastung gilt dass die Breite und Höhe der Chrominanzanteile zu der Breite und Höhe des Luminanzanteils immer in einem proportionalen, ganzzahligen Verhältnis stehen müssen.
Überführung in den Frequenzbereich
Der nun folgende Schritt ist für den Laien sicherlich einer, der nicht einfach nachzuvollziehen ist: Die Bilddaten werden aus der Ortsdomäne, dem Raum der Pixel, in die Frequenzdomäne, den Raum der gewichteten Schwingungen, überführt. Bevor mit der Überführung begonnen werden kann, ist noch ein kleiner, simpler Schritt notwendig: Die Y, Cb und Cr Farbanteile werden in kleine Quadrate der Größe 8x8 Pixel unterteilt.

Abbildung 10: Unterteilung des Luminanz-Anteils in Bildblöcke der Größe 8x8.
(Ausschnitt, Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Auf Bildquadraten dieser Größe baut die 8x8 DCT ('Discrete Cosinus Transformation') Transformation, welche für die Überführung zuständig ist, auf. Sie kann nur auf Blöcke der Größe 8x8 angewandt werden, daher behilft sich das JPEG-Verfahren einer Notlösung falls die Unterteilung nicht aufgeht, die Pixelzahl der Bildbreite oder -höhe also nicht ein Vielfaches von acht ist. Bildbreite und Bildhöhe werden dann intern auf ein Vielfaches von acht aufgerundet und die hinzugekommenen Pixel mit beliebigen Werten gefüllt. Für den Betrachter sind diese zusätzlichen Pixel nicht sichtbar, sie werden bei der Dekompression wieder abgeschnitten.
Die DCT Transformation basiert auf einer Formel, welche auf die Intensitätswerte aller 64 Pixel eines 8x8 Blockes angewandt wird. Ihr Ergebnis ist wiederum ein Raster aus 8x8 Werten, welche Intensitätswerte nicht von Pixeln, sondern von bestimmten auf Cosinuskurven basierenden Basisbildern repräsentieren (siehe Abbildung 11). Diese Intensitätswerte werden DCT-Koeffizienten genannt. Das ursprüngliche Bild kann durch Überlagerung der Basisbilder des Frequenzspektrums wieder erzeugt werden, wenn dabei die durch die DCT Koeffizienten gegebene Gewichtung der Überlagerungsintensität für das jeweiligen Basisbild berücksichtigt wird.

Abbildung 11: Die 64 auf Cosinuskurven basierenden Basisbilder des Frequenzspektrums.
(Quelle: Wikimedia Commons)
Der Anteil an der linken oberen Ecke des Frequenzspektrums an Position (0/0) ist ein Sonderfall. Es wird Gleichstrom- oder DC-Anteil (DC: direct current) genannt und repräsentiert die mittlere Helligkeit des ursprünglichen 8x8 Bildblockes. Die übrigen 63 Anteile werden Wechselstrom- oder AC-Anteile (AC: alternating current) genannt und repräsentieren Schwingungen in unterschiedlicher Frequenz horizontaler und vertikaler Richtung.
Einfach ausgedrückt sind AC-Anteile in der linken oberen Ecke des Spektrums für grobe Strukturen, AC-Anteile in der linken unteren Ecke für feine Details im Bildblock zuständig (siehe hierzu Abbildung 12). In natürlichen Bildern treten, auch aufgrund der Unzulänglichkeiten moderner Photosensoren, grobe Strukturen mit größerer Intensität als feine Details auf, nach rechts unten hin nehmen die DCT Koeffizienten in ihrer Betragshöhe daher üblicherweise ab. Dieses Verhalten unterscheidet sich stark von dem Verhalten der Pixelintensitäten, die zumeist über den gesamten 8x8 Block Werte ähnlicher Höhe annehmen.

Abbildung 12: Testbild zusammengesetzt aus (link-oben) nur DC Anteil, (rechts-oben) ersten 2x2 Anteilen, (links-unten)
ersten 4x4 Anteilen und (rechts-unten) vollständigem Frequenzspektrum.
Jeder hinzugekommene AC Anteil fügt dem Bild eine weitere Schicht an Detailreichtum hinzu.
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Für den interessierten Leser sei an dieser Stelle auch der mathematische Hintergrund der Transformation erklärt: Seien fmn Intensitätswerte von Pixeln an der Position (m/n) im 8x8 Bildblock, Fxy DCT Koeffizienten an Position (x/y) im 8x8 Raster. Die DCT Koeffizienten werden dann durch folgende Formel errechnet:
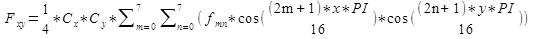
Cx und Cy werden durch eine einfache Fallunterscheidung bestimmt:
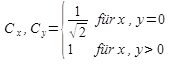
Rechnet man die Formel für alle x von 0 bis 7 und alle y von 0 bis 7 durch, so ergeben sich die 64 DCT Koeffizienten, welche den ursprünglichen 8x8 Bildblock in der Frequenzdomäne darstellen.
Die inverse Transformation, auch IDCT ('inverse DCT') Transformation genannt, welche DCT Koeffizienten Fxy wieder in Intensitätswerte von Pixeln fmn überführt, besteht ebenfalls aus einer Formel:
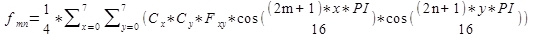
Für Cx und Cy gilt wiederum dieselbe Fallunterscheidung wie für die vorherige Formel. Die DCT ist eine völlig verlustfreie Transformation - mit Hilfe der Formel und den unveränderten DCT Koeffizienten können alle 64 Intensitätswerte der Pixel an den jeweiligen Positionen (m/n) (m von 0 bis 7 und n von 0 bis 7) im Bildblock wieder eindeutig rekonstruiert werden.
Steuerung von Qualität und Dateigröße: Quantisierung
Durch die DCT Transformation alleine ist nichts gewonnen, ganz im Gegenteil sogar: Statt relativ überschaubaren ganzzahligen Pixelwerten mit einem Wertebereich von 0 bis 255 sind durch die Transformation DCT Koeffizienten entstanden, welche durch Dezimalzahlen mit einem Wertebereich von -1024 bis 1018 repräsentiert werden. Um die durch die DCT Transformation erkämpften Vorteile auch zu nutzen, bedarf es eines weiteren Schrittes: Der Quantisierung.
Die Grundlage der Quantisierung ist wiederum das menschliche Wahrnehmungssystem. Menschen nehmen Bilder nicht auf Basis von Bildpunkten (diese sind nur die Grundlage für die Speicherung und Darstellung digitaler Bilder) wahr, sondern erkennen stattdessen Flächen, Muster und Übergänge – der einzige Bildpunkt spielt dabei höchstens eine untergeordnete Rolle. Zum Vorteil des JPEG Verfahrens ist die menschliche Wahrnehmung gerade gegenüber sehr feinen Details, wie sie von den Basisbildern im unteren rechten Teil des Frequenzspektrums repräsentiert werden, relativ unempfindlich. Die DCT Koeffizienten, welche die Überlagerungsintensität der Basisbilder steuern, können daher manipuliert werden, ohne das dies dem menschlichen Betrachter auffällt.
Bei der Quantisierung werden die zuvor errechneten DCT Koeffizienten durch bestimmte Quantisierungsfaktoren geteilt und anschließend zum nächsten ganzzahligen Wert gerundet. Bei der Rückrechnung muss requantisiert werden: Die quantisierten DCT Koeffizienten müssen wieder mit den Quantisierungsfaktoren multipliziert werden, um DCT Koeffizienten im ursprünglichen Wertebereich zu erhalten. Bei diesem Prozess geht Genauigkeit verloren, und es entstehen Abweichungen zwischen dem unverarbeiteten Originalbild und seiner Repräsentation als komprimiertem JPEG Bild (siehe Abbildung 13).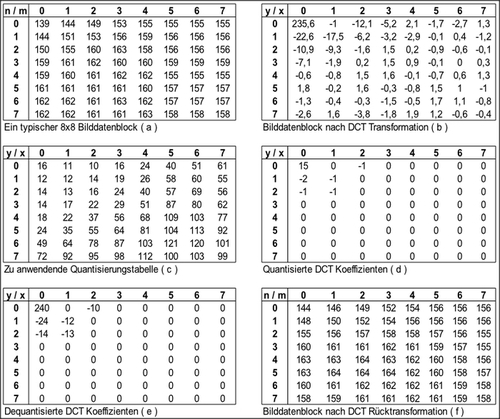
Abbildung 13: Ein typischer Bilddatenblock (a) nach DCT Transformation (b), Quantisierung (d), Requantisierung
(e) und Rücktransformation (f). Es wird Quantisierungstabelle (c) verwendet. Zwischen ursprünglichem Block (a)
und rekonstruiertem Block (f) sind kleinere Unterschiede zu erkennen.
Damit diese Abweichungen nicht auffallen, wird nicht jeder der 8x8 DCT Koeffizienten durch denselben Quantisierungsfaktor geteilt und stattdessen eine Quantisierungstabelle genutzt, welche innerhalb der JPEG-Datei gespeichert wird. Die Tabelle enthält 64 Quantisierungsfaktoren, welche in etwa die Empfindlichkeit der menschlichen Wahrnehmung gegenüber dem jeweils korrespondierenden Frequenzanteil repräsentieren. Üblicherweise werden, um die Unzulänglichkeiten bei der Farbwahrnehmung nochmals speziell zu nutzen, für Luminanz- und Chrominanzenanteile jeweils eigene Quantisierungstabellen verwendet. Obwohl bereits im Rahmen der Normierung des Standards umfangreiche Untersuchungen zur Bestimmung optimaler Quantisierungstabellen durchgeführt wurden, und der Standard entsprechende Tabellen bereitstellt, optimieren auch heute noch verschiedene Kamerahersteller ihre Tabellen auf Basis verschiedener Versuchsreichen mit mehreren Testpersonen.
Die Quantisierungstabelle ist ein Mittel zur Schaffung eines Kompromisses zwischen Dateigröße und Darstellungsqualität. Wie der Leser in den folgenden Abschnitten erkennen wird, ermöglichen höhere Quantisierungsfaktoren größere Einsparungen bei der Dateigröße. Diese Einsparungen kommen zum Preis schlechterer Qualität bei der Darstellung. Werden die Quantisierungsfaktoren zu hoch gewählt, so entstehen für den Betrachter sichtbare Blockartefakte, und der Detailreichtum des dargestellten Bildes nimmt sichtlich ab.
Durch die Verwendung eines geeigneten Testbildes höchster Qualität kann diese Verschlechterung besonders gut veranschaulicht werden. Ein solches Testbild wurde von der Firma Burosch Audio-Video-Technik unter hohem Aufwand erstellt und für die Verwendung in diesem Artikel bereitgestellt (siehe Abbildung 14).
Abbildung 14: Sichtbare Qualitätsverschlechterung bei Wahl gröberer Quantisierungstabellen
(Bild bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de, Qualität angepasst mit IrfanView, www.irfanview.com/)
Abbildung 15: JPEG-Qualitätseinstellungen bei Adobe Photoshop - Die Quantisierungstabellen werden über die 12-stufige 'Quality'-Einstellung gewählt.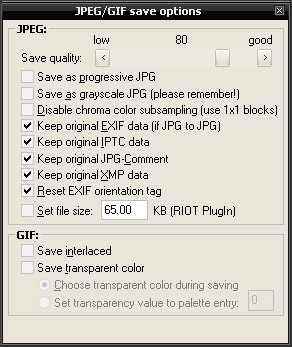
Abbildung 16: JPEG-Qualitätseinstellungen bei IrfanView - Die Quantisierungstabellen werden über die 100-stufige 'Save quality'-Einstellung gewählt,
oder alternativ durch Eingabe der gewünschten Dateigröße.
Ein Kamerahersteller wird seine Quantisierungstabellen in aller Regel so wählen, dass für den Nutzer keinerlei Qualitätsverlust ersichtlich ist. Oftmals werden in den Kameraeinstellungen zwei verschiedene Qualitätseinstellungen, 'high' und 'low', angeboten, wobei 'high' für die beste mögliche Qualität bei großer Dateigröße, 'low' für einen guten Kompromiss zwischen geringen Abstrichen bei der visuellen Qualität und der Dateigröße steht. Es existieren auch solche Fälle, in denen Speicher ein wichtigeres Gut darstellt als visuelle Qualität – man denke z.B. an mobile Datenverbindungen mit geringer Bandbreite. Die meisten Bildbearbeitungsprogramme bieten daher beim Speichern in eine JPEG-Datei eine stufenweise Qualitätseinstellung an, über die die Wahl der Quantisierungstabelle und damit indirekt Qualität und Dateigröße gesteuert wird (siehe Abbildungen 15 und 16).
Intelligente Reorganisation und Differenzkodierung
Intern werden die quantisierten DCT Koeffizienten nicht im zweidimensionalen Raster, sondern in einer eindimensionalen Reihe gespeichert. Bei der Umsortierung kommt der Zickzack-Scan zum Einsatz, welche links oben beim DC Koeffizienten beginnt und die AC Koeffizienten in einem Zickzack-Muster durchläuft (siehe Abbildung 17). Der Zickzack-Scan ordnet die Koeffizienten in etwa nach ihrer durchschnittlichen Betragshöhe an.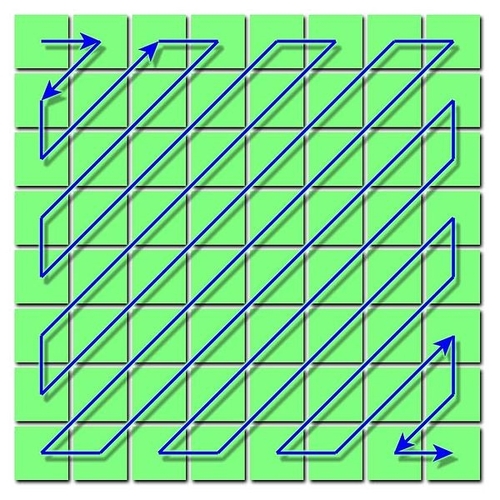
Abbildung 17: Zickzack-Reihenfolge der quantisierten Koeffizienten (Quelle: Wikimedia Commons)
Ein Beispiel soll die Reorganisation der Koeffizienten veranschaulichen. Es werden die quantisierten Koeffizienten aus dem vorherigen Abschnitt (in Abbildung 13) verwendet und im Zickzack-Scan aufgereiht:
15, 0, -2, -1, -1, -1, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
Vor allem auffällig an dieser Zahlenfolge sind die vielen Nullen am Ende. Der Leser wird hier höchstwahrscheinlich nur den ersten neun Zahlen Beachtung schenken, den Rest anschließend überlesen. Es ist auch nicht notwendig, 57 mal die Zahl Null zu lesen, denn schließlich genügt es zu sehen dass ab der zehnten Stelle nichts Interessantes mehr folgt.
Im JPEG Verfahren existiert für genau diesen Fall ein spezielles Symbol, das EOB (End-of-Block) Symbol. Das EOB Symbol wird überall dort verwendet, wo in einem gegebenen Block ab einer bestimmten Stelle nur noch Nullen folgen. Da jederzeit bekannt ist, dass ein Block immer aus 64 Koeffizienten besteht, kann ein EOB Symbol bei der Rückrechnung wieder in die genaue Anzahl Nullen übersetzt werden, welche es zuvor substituierte.
Unter Verwendung des EOB Symbols kann die zuvor gezeigte Zahlenreihe auf kleinerem Raum ausgedrückt werden:
15, 0, -2, -1, -1, -1, 0, 0, -1, (EOB)
Nach der Quantisierung ist die Null ist der häufigst vorkommende Wert eines DCT Koeffizienten. Es kommt daher die Lauflängenkodierung ('RLE', 'Run-Length-Encoding'), ein Standardverfahren der Datenkompression, zum Einsatz. Nach dem Prinzip der Lauflängenkodierung werden alle Nicht-Null Koeffizienten als Wertepaare (r|v) kodiert, wobei r für die Anzahl der Nullen direkt vor dem Koeffizienten, v für den Wert des Koeffizienten steht. Ausgenommen von dieser Behandlung ist der DC Koeffizient, da er nur selten den Wert Null annimmt.
Wendet man die Lauflängenkodierung auf das Beispiel an, so ergibt sich folgende Reihe:
(15), (1|-2), (0|-1), (0|-1), (0|-1), (2|-1), (EOB)
Durch intelligente Reorganisation konnten also im Beispiel die zuvor 64 Koeffizienten des 8x8 Rasters auf nur sieben Symbole (DC Koeffizient, fünf Wertepaare, EOB Symbol) reduziert werden. Die Ergebnisse im Einzelfall hängen vom Bild und den genutzten Quantisierungstabellen ab. Mehr Nullen im Block (welche durch stärkere Quantisierung begünstigt werden) bedeuten weniger notwendige Symbole zur Darstellung und damit stärkere Kompression.
Nach der Reorganisation folgt ein letzter Schritt. DC Koeffizienten benachbarter Blöcke sind sich meist untereinander sehr ähnlich. Wie bereits erwähnt repräsentieren sie die Grundhelligkeit über den gesamten Block, welche in natürlichen Bildern unter benachbarten Blöcken üblicherweise nur in geringem Ausmaß schwankt. DC Koeffizienten werden daher differenzkodiert, das heißt statt des Koeffizienten wird die Differenz zwischen dem Koeffizienten und seinem linken Nachbarn zur weiteren Verarbeitung verwendet. Da der erste DC Koeffizient des Blockes links oben von dieser Verarbeitung ausgeschlossen ist (schließlich hat er auch keinen linken Nachbarn) kann aus Differenz und jeweils linkem Nachbarn beim Dekodieren einfach wieder der ursprüngliche Koeffizient errechnet werden.
Angenommen der DC Koeffizient des linken Nachbars des Beispielblockes (der Beispielblock wurde bislang für sich, außerhalb seiner Nachbarschaft betrachtet) wäre 14, dann ergäbe sich nach Reorganisation und Differenzkodierung folgende Reihe:
(1), (1|-2), (0|-1), (0|-1), (0|-1), (2|-1), (EOB)
Die Diffferenzkodierung reduziert nicht die Zahl der zur Darstellung benötigten Symbole, sondern die Betragshöhe des DC Koeffizienten. Den Nutzen dieser Maßnahme wird der folgende Abschnitt erläutern.
Huffman-Kodierung
DCT Koeffizienten folgen üblicherweise einer charakteristischen Verteilung: In typischen Fällen treten niedrige Beträge bei AC Koeffizienten und differenzkodierten DC Koeffizienten deutlich häufiger auf als hohe Beträge – die 0 ist der häufigste Wert eines DCT Koeffizienten, danach folgen 1/-1, 2/-2, 3/-3, ... mit abfallenden Häufigkeiten. Durch die Quantisierung wird diese Verteilung begünstigt, man kann sie aber schon vor der Quantisierung beobachten.
Ein ähnliches Verhalten kann auch bei den Nullen-Läufen beobachtet werden: Läufe der Länge 0 sind am häufigsten, danach folgen Läufe der Längen 1, 2, 3, 4, 5... in absteigender Reihenfolge. Die Häufigkeit mit der die jeweiligen (Lauflängen|DCT Koeffizient) Symbole auftreten ist stark unterschiedlich - Symbole wie (0|1) treten sehr häufig auf, Symbole wie (15|777) eher selten oder sogar nie. Den untereinander stark schwankenden Häufigkeiten wird Rechnung getragen, indem die Symbole Huffman-kodiert in der Datei gespeichert werden.
Die Huffman-Kodierung ist ein universelles Verfahren der Datenkompression. Sie kommt zum Einsatz in so bekannten Archivierungsformaten wie ZIP oder RAR sowie in anderen komprimierten Medienformaten wie MP3. Huffman-Kodierung nutzt den Umstand, dass unterschiedliche Symbole mit unterschiedlichen Häufigkeiten auftreten: Die Symbole können platzsparend gespeichert werden, indem häufig auftretende Symbole mit niedrigen Bitlängen und selten auftretende Symbole dafür mit höheren Bitlängen kodiert werden. Jedem vorkommenden Symbol wird entsprechend seiner Häufigkeit eine bestimmte Bitfolge zugewiesen. Anstatt der eigentlichen Symbole werden dann nur die jeweiligen Bitfolgen in der Datei gespeichert, wodurch das Datenvolumen verringert wird. Bei der Dekodierung werden die Bitfolgen wieder in die ursprünglichen Symbole übersetzt. Die Zuweisung zwischen Symbol und Bitfolge wird in einer Huffman-Tabelle gespeichert, welche entweder als bekannt vorausgesetzt wird oder innerhalb der Datei gespeichert werden muss, damit der kodierte Datenstrom wieder dekodiert werden kann.
Symbole im JPEG Verfahren werden in einem zweistufigen Verfahren kodiert: Zunächst wird mit einer bestimmten Huffman-Tabelle (a) die Länge des Nullen-Laufs (diese entfällt für DC Koeffizienten) und die Bitlänge des Koeffizientenbetrages kodiert (siehe hierzu auch Abbildung 18), anschließend wird mittels der Bitlänge eine andere Huffman-Tabelle (b) ausgewählt und der eigentliche Koeffizient kodiert. Alle Huffman-Tabellen (b) sind bereits fest vom Verfahren vorgegeben und müssen nicht in der Datei gespeichert werden. Alle Huffman Tabellen (a) werden im Header der JPEG-Datei gespeichert. Für jeden Farbanteil (Y, Cb und Cr) können jeweils zwei unterschiedliche Huffman-Tabellen (a), eine für den DC, eine für den AC Anteil, genutzt werden.
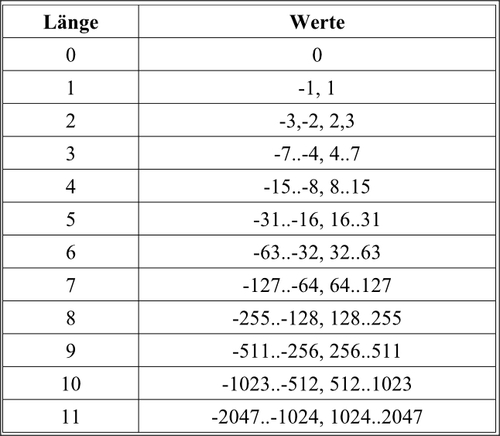
Abbildung 18: Mögliche Bitlängen von DCT Koeffiziente.
Das zweistufige Verfahren hat im wesentlichen zwei Vorteile: Einerseits wird im Header Platz gespart, da alle Huffman-Tabellen (b) nicht gespeichert werden müssen (diese hätten ansonsten eine beachtliche Größe), andererseits bieten die im Header zu speichernden Huffman-Tabellen (a) Optimierungsmöglichkeiten, denn diese können an die zu komprimierenden Symbole angepasst werden. JPEG-Dateien, die mit angepassten Tabellen erzeugt wurden, sind in der Regel um etwa 2% kleiner als solche die ohne Optimierung der Tabellen erzeugt wurden.
Baseline, Sequentiell, Progressiv
Nachdem nun alle wichtigen Schritte auf dem Weg vom Photosensor oder unkomprimierten RGB-Bild zum komprimierten JPEG erklärt sind, sind dennoch einige wichtige Begriffe offen. Jeder, der sich schon einmal eingehend mit dem JPEG-Format beschäftigt hat kennt die Begriffe Baseline, Sequentiell und Progressiv, was aber steckt hinter diesen Begriffen?
Baseline, Sequentiell und Progressiv beschreiben drei Modi, die steuern, wie innerhalb der JPEG-Datei der kodierte Datenstrom organisiert und gespeichert ist. Die häufigst genutzte Form ist der Baseline Modus. Dieser organisiert die Daten innerhalb des kodierten Datenstroms in MCUs ('Minimum Coded Units'). Eine MCU enthält zwei zueinander gehörige 8x8 Blöcke der beiden Chrominanzanteile und alle 8x8 Blöcke des Luminanzanteils, die zu den Chrominanzblöcken korrespondieren. Bei Farbunterabtastung 4:2:0 wären das vier, bei 4:2:2 zwei, bei 4:4:4 jeweils ein 8x8 Block der Luminanz auf einen Cb oder Cr 8x8 Block (siehe Abbildung 19). Im Baseline Modus sind die Daten sequentiell gespeichert – die MCUs werden von links nach rechts und von oben nach unten in die Datei geschrieben.
JPEG-Dateien, die in einem sequentiellen Modus gespeichert sind, sind daran erkennbar, dass sie sich z.B. bei einer langsamen Internetverbindung immer zeilenweise aufbauen. Für den Baseline Modus gilt eine wichtige Einschränkung: Es dürfen nur zwei unterschiedliche Quantisierungstabellen (eine für die Luminanz, eine für beide Chrominanzen) und vier unterschiedliche Huffman-Tabellen (jeweils zwei für Luminanz und die beiden Chrominanzen, eine davon für den DC-Anteil, eine für beide AC-Anteile) verwendet werden. Der sequentielle Modus, intern 'extended sequential' Modus genannt, unterscheidet sich vom Baseline Modus ausschließlich durch die Aufhebung dieser Limitation. Nur in diesem Modus können daher separate Quantisierungs- und Huffman-Tabellen für die beiden Chrominanzen definiert werden.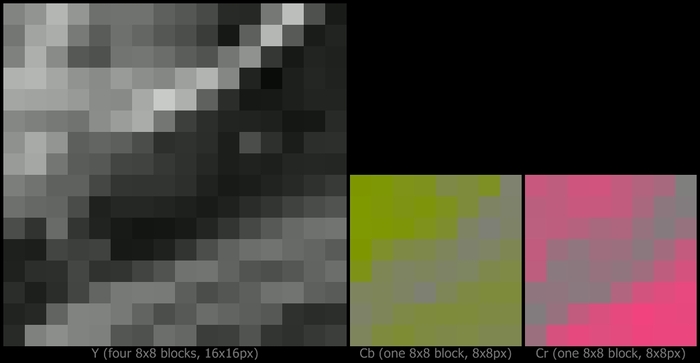
Abbildung 19: Eine MCU bei Farbunterabtastung 4:2:0.
(Ausschnitt bereitgestellt durch Fa. Burosch Audio-Video-Technik, www.burosch.de)
Der vielseitigste Modus im JPEG Verfahren ist der progressive Modus. In diesem Modus wird die genaue Organisation der Daten durch umfangreiche Einstellungen gesteuert. Der progressive Modus bietet viele Möglichkeiten:
- Ein in MCUs verschachtelter zeilenweiser Aufbau wie bei den sequentiellen Modi oder...
- ...spektrale Selektion: zunächst nur den DC oder die ersten n Koeffizienten im Zickzack-Scan für das gesamte Bild in die Datei zu schreiben, anschließend die Koeffizienten an den übrigen Positionen oder...
- … die Trennung der Farbanteile: zunächst den vollständigen Y-Anteil, dann den Cb-Anteil, dann den Cr-Anteil zu schreiben oder...
- … die sukzessive Approximation: es werden zunächst die oberen m Bits aller Koeffizienten geschrieben, danach Schritt für Schritt die unteren Bits nachgetragen oder...
- … eine beliebige Kombination der genannten Möglichkeiten.
Wählt man in einem Bildbearbeitungsprogramm den progressiven Modus zur Speicherung im JPEG-Format, so werden diese Einstellungen üblicherweise nicht dem Nutzer überlassen, sondern automatisch vorgenommen. Zumeist wird dabei eine Kombination aus spektraler Selektion und sukzessiver Approximation genutzt, was dann letztendlich zu dem für progressive JPEGs charakteristischen Aufbau, der schrittweisen Verfeinerung von Bilddetails führt (vergleiche dazu auch Abbildung 12).
Wie im 'extended sequential' Modus gibt es im progressiven Modus keinerlei Limitationen hinsichtlich der Quantisierungs- und Huffman-Tabellen, bei schrittweisem Aufbau können die Huffman-Tabellen sogar mit jedem Schritt jeweils neu definiert werden. Aufgrund der vielfältigen Optimierungsmöglichkeiten sind progressive JPEG-Dateien typischerweise etwa 8% kleiner als entsprechende in sequentiellen Modi gespeicherte Dateien, dennoch wird auf den progressiven Modus üblicherweise verzichtet, da einige ältere JPEG-Decoder progressive JPEGs nicht anzeigen können.
Literaturempfehlungen & Quellen
Die im Bericht verwendeten Bilder wurden, außer dort wo anderweitig gekennzeichnet, von der Firma Burosch Audio-Video-Technik bereitgestellt. Die Firma ist im WWW zu finden unter: www.burosch.de.
Teil 2 dieses Berichtes mit dem Titel 'JPEG – Das Bildformat – Teil 2: Praxis' finden Sie auf den Seiten der Firma Burosch unter www.burosch.de.
Für weitere, über diesen Bericht hinausgehende Informationen zum JPEG-Format seien dem Leser folgende Werke empfohlen:
''JPEG: still image data compression standard'' von Joan L. Mitchell und William B. Pennebaker (ISBN-13: 978-0442012724): Ein umfassendes Nachschlagewerk auf 650 Seiten, welches jeden Aspekt im Detail erläutert.
''The JPEG still picture compression standard'' von Gregory K. Wallace, erschienen in Communications of the ACM, Vol. 43, Iissue 4, April 1991: Eine detailierte Kurzübersicht zum Thema.
''Wikipedia: JPEG'' von verschiedenen Autoren, en.wikipedia.org/wiki/JPEG
Über diesen Link bekommen Sie eine PDF mit allen Bildern in hoher Auslösung.
Technischer Redakteur:
Matthias Stirner
Copyright 2011 – All rights reserved
