Die Wellenzahl 'k'
In unseren aktuellen Testbildern wird zur Beschreibung der Intensität von Frequenzen in wellenförmige Signalverläufen die Einheit 'k' statt der geläufigeren Einheit 'Hz' bzw. 'MHz' genutzt. Wir erklären Ihnen in diesem Dokument warum wir uns für diese Einheit entschieden haben, die Herkunft und die Bedeutung der Wellenzahl k.
Wellenförmige Signalverläufe
Eine Angabe über die Frequenz eines Signalverlaufs kann überall dort getroffen werden, wo dieser Signalverlauf wellenförmig ist. Zutreffend ist dies bei einem auf der Sinus- oder Kosinus-Funktion basierende Wechsel von Helligkeitswerten im Testbild oder auch bei regelmäßig verlaufenden sonstigen Wechseln der Pixelwerte.

Ein solcher Signalverlauf liegt z.B. vor bei dem oben gezeigten Ausschnitt aus unserem 'Sweep Steps' Testbild. Die horizontal veränderlichen Helligkeitswerte des Ausschnitts basieren auf der Kosinusfunktion. Die Frequenz für die Horizontale kann mit der Wellenzahl k angegeben werden.

Auch die Helligkeitswerte unser 'Cosine Circles' Testbild basieren auf der Kosinus-Funktion, der Signalverlauf ist vom Zentrum ausgehend in alle Richtungen wellenförmig. Die Wellenzahl k kann nicht nur für die Horizontale, sondern für alle Richtungen zur Angabe der Frequenz genutzt werden.

Ein Schachbrettmuster besteht aus sich regelmäßig abwechselnden Schwarz-Weiß-Pixeln. Auch hierfür kann die Wellenzahl k zur Angabe der Frequenz genutzt wurden, es muss jedoch zuvor geklärt werden ob die Frequenz für die Horizontale, die Vertikale oder die 45° Diagonale angegeben wird.
Definition der Wellenzahl 'k'
Die Wellenzahl 'k' stammt ursprünglich aus der Signaltheorie und wird zur Beschreibung wellenförmiger Signalverläufe in pixelbasierten Daten verwendet. Sie ist verwandt mit der Einheit 'Hertz' ('Hz'), basiert jedoch auf dem Pixel als Basiseinheit anstatt der Zeit.
Die Wellenzahl k ist der Kehrwert der Wellenlänge λ (gesprochen 'lambda'). Die Wellenlänge λ wiederum beschreibt die Länge einer Periode (also einer vollständig abgeschlossenen Welle) in Pixeln.
Mathematisch ausgedrückt ist der Zusammenhang zwischen Wellenzahl k und Wellenlänge λ dieser: k = 1 / λ.
Einfacher lässt sich dieser Zusammenhang am Beispiel erklären. Schauen Sie sich hierzu diese Grafik an:
![]()
Sie sehen horizontal wechselnde weiße und schwarze Pixel. Das Muster wiederholt sich jeweils nach 2 Pixeln, die Periodenlänge ist also 2 Pixel:
λ = 2px
Während λ die Antwort auf die Frage 'Wie lang ist eine Welle?' liefert, liefert k die Antwort auf die Frage 'Wieviele Wellen gibt es pro Pixel?'. Entsprechend wird k aus dem Kehrwert von λ errechnet:
λ = 2px → freq = 1/λ = ½k = 0,5k
Wie Sie sehen entspricht eine Periodenlänge von 2 Pixeln einer Frequenz von 0,5k.

Die obige Grafik zeigt Ihnen verschiedene Signalverläufe mit Periodenlängen von 2/4/8/16/32px und die jeweils zugehörige mit k gemessene Frequenz.
Für nicht strikt horizontale bzw. vertikale periodische Signalverläufe muss zusätzlich beachtet werden, dass grundsätzlich der tatsächliche Pixelabstand der Frequenzangabe zugrunde gelegt werden muss.
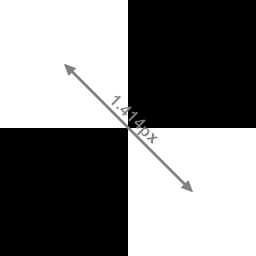
In der obigen Grafik z.B. beträgt der Abstand zwischen den beiden weißen Pixeln exakt √2 ≈ 1,414px. Angenommen dieser Ausschnitt ist Teil eines wellenförmigen Signalverlaufs, so beträgt die Frequenz dieses Signalverlaufs im 45° Grad Winkel ca. 0,707k.
Warum k statt MHz?
Die Einheit MHz hat für unsere Zwecke den Nachteil, dass diese zeitbasiert und dadurch abhängig von der Bildwiederholfrequenz des Ausgabemediums ist. Zeigen Sie unser Full-HD-Testset auf einem Full-HD-fähigen TV-Gerät an, so wäre die Frequenz in MHz eine andere als bei der Ausgabe auf dem Computermonitor, obwohl die jeweilige Bilddatei exakt die gleiche wäre.
Das Problem der Abhängigkeit vom Ausgangsmedium wird durch die durchgängige Verwendung der Wellenzahl k zur Angabe von Frequenzen behoben, indem Frequenzen nun in Abhängigkeit von Pixeln beschrieben werden. Durch die Wellenzahl k haben Sie die Garantie dass – völlig unabhängig vom Ausgabemedium – Sie immer eine korrekte Angabe der Frequenz haben.
Quellen
Nischwitz A., Fischer M., Haberäcker P.; 'Computergrafik und Bildverarbeitung'; Erschienen im Vieweg+Teubner Verlag; ISBN-13: 978-3834801869
Verschiedene Autoren; 'Wikipedia: Wellenzahl'; http://de.wikipedia.org/wiki/Wellenzahl
Impressum
BUROSCH Audio-Video-Technik
Inhaber: Klaus Burosch
Sigmaringer Str. 20
70567 Stuttgart / Germany
www.burosch.de
Technischer Redakteur
Matthias Stirner
Copyright 2013 – All rights reserved
